We find the \(y\)-intercept by finding the value for \(f(0)\).
\begin{align*}
f(x) & = x^{3} -9x^{2} + 24x - 20 \\
f(0) & = (0)^{3} - 9(0)^{2} + 24(0) - 20\\
& = -20
\end{align*}
The \(y\)-intercept is: \((0;-20)\)
We find the \(x\)-intercepts by finding the values for which the
function \(f(x) = 0\).
We use the factor theorem to check if \((x-1)\) is a factor.
\begin{align*}
f(x) & = x^{3} -9x^{2} + 24x - 20 \\
f(1) & = (1)^{3} - 9(1)^{2} + 24(1) - 20 \\
& = -4
\end{align*}
Therefore, \((x-1)\) is not a factor.
We now use the factor theorem to check if \((x+1)\) is a factor.
\begin{align*}
f(x) & = x^{3} -9x^{2} + 24x - 20 \\
f(-1) & = (-1)^{3} - 9(-1)^{2} + 24(-1) - 20 \\
& = -54
\end{align*}
Therefore, \((x+1)\) is not a factor.
We now try \((x-2)\):
\begin{align*}
f(x) & = x^{3} -9x^{2} + 24x - 20 \\
f(1) & = (2)^{3} - 9(2)^{2} + 24(2) - 20 \\
& = 0
\end{align*}
Therefore, \((x-2)\) is a factor.
If we divide \(f(x)\) by \((x-2)\) we are left with:
\[f(x) = (x-2)(x^{2} - 7x + 10)\]
This has factors:
\[f(x) = (x-2)(x-5)(x-2)\]
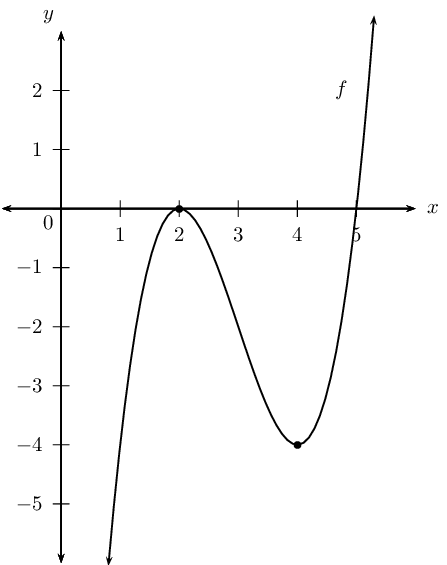
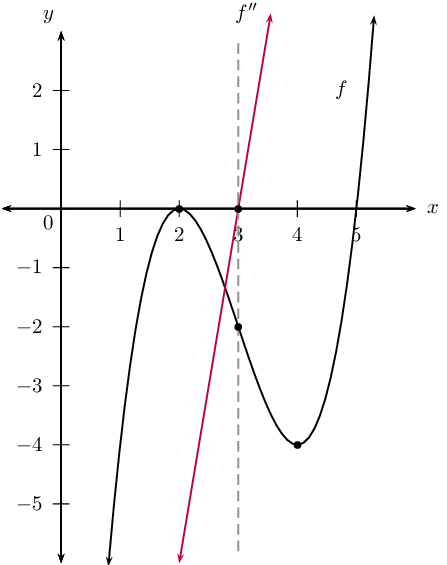
The \(x\)-intercepts are: \((2;0), (5;0)\).
Find the turning points by setting \(f'(x)=0\).
If we use the rules of differentiation we get:
\begin{align*}
f'(x) & = 3x^{2} - 18x + 24 \\
0 & = 3(x^{2} - 6x + 8) \\
& = 3(x-2)(x-4)
\end{align*}
The \(x\)-coordinates of the turning points are: \(x=4\) and \(x=2\).
The \(y\)-coordinates of the turning points are calculated as:
\begin{align*}
f(2) & = (2)^{3} - 9(2)^{2} + 24(2) - 20 \\
& = 0
\end{align*}
and
\begin{align*}
f(4) & = (4)^{3} - 9(4)^{2} + 24(4) - 20 \\
& = -4
\end{align*}
Therefore the turning points are: \((2;0)\) and \((4;-4)\).