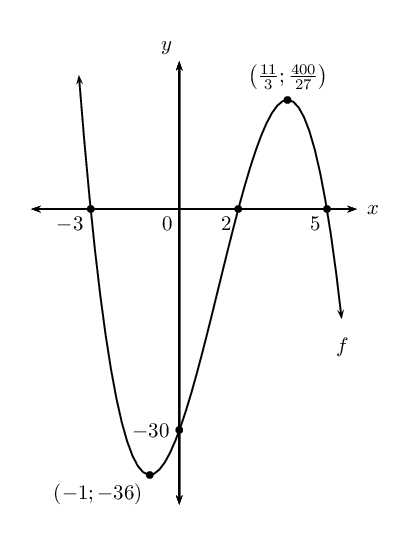
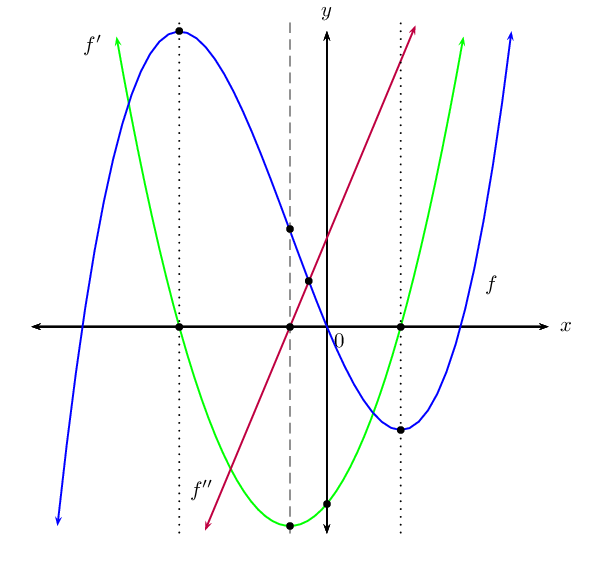
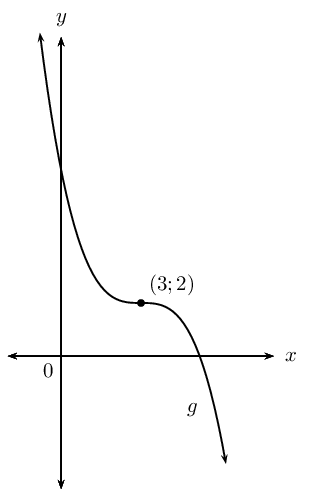
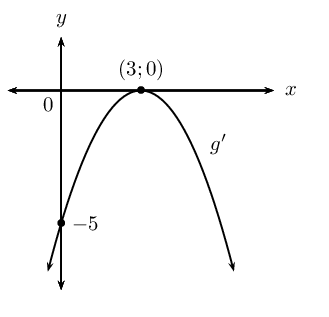
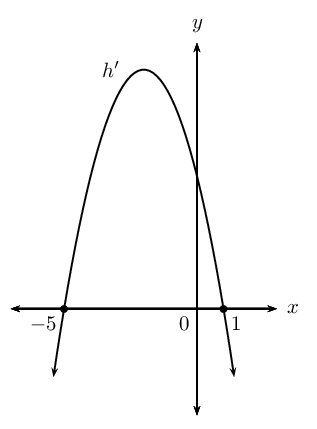
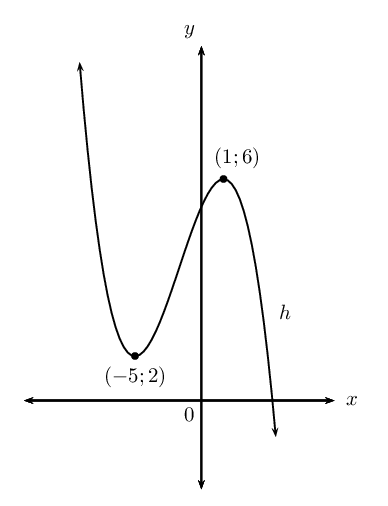
We find the \(y\)-intercept by letting \(x = 0\):
\begin{align*}
f(x) & = -x^{3} +4x^{2} +11x - 30 \\
f(0) & = -(0)^{3} + 4(0)^{2} +11(0) - 30\\
& = -30
\end{align*}
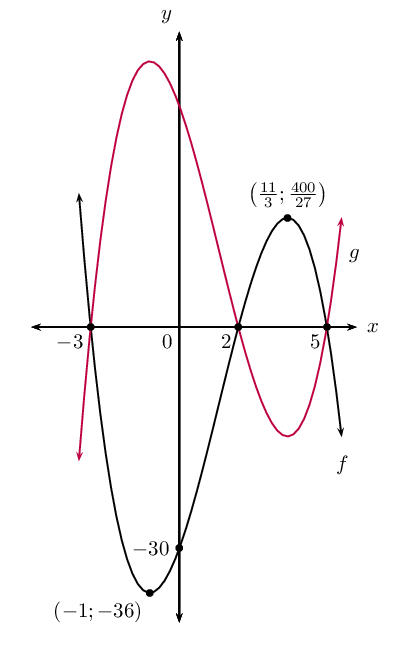
The \(y\)-intercept is: \((0;-30)\)
We find the \(x\)-intercepts by letting \(f(x) = 0\).
We use the factor theorem to check if \((x-1)\) is a factor.
\begin{align*}
f(x) & = -x^{3} + 4x^{2} + 11x - 30 \\
f(1) & = -(1)^{3} + 4(1)^{2} + 11(1) - 30 \\
& = -16
\end{align*}
Therefore, \((x-1)\) is not a factor.
We now use the factor theorem to check if \((x+1)\) is a
factor.
\begin{align*}
f(x) & = -x^{3} + 4x^{2} + 11x - 30 \\
f(-1) & = -(-1)^{3} + 4(-1)^{2} + 11(-1) - 30 \\
& = -36
\end{align*}
Therefore, \((x+1)\) is not a factor.
We now try \((x-2)\):
\begin{align*}
f(x) & = -x^{3} + 4x^{2} + 11x - 30 \\
f(2) & = -(2)^{3} + 4(2)^{2} + 11(2) - 30 \\
& = 0
\end{align*}
Therefore, \((x-2)\) is a factor.
\begin{align*}
f(x) & = (x-2)(-x^{2} + 2x + 15) \\
& = -(x-2)(x^{2} - 2x - 15) \\
& = - (x - 2)(x + 3)(x - 5)
\end{align*}
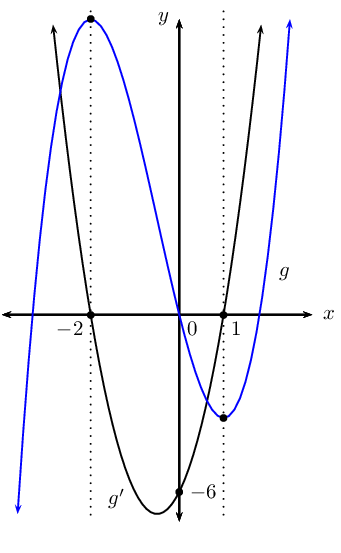
The \(x\)-intercepts are: \((2;0), (-3;0), (5;0)\).
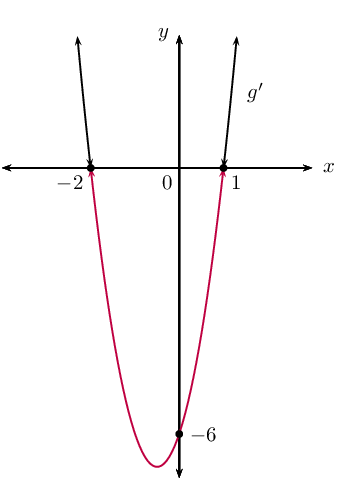
For the turning points, let \(f'(x)=0\).
\begin{align*}
f'(x) & = -3x^{2} + 8x + 11 \\
&= -(3x^{2}-8x-11) \\
\therefore 0 & = (3x-11)(x+1)
\end{align*}
The \(x\)-coordinates of the turning points are: \(x=-1\) and
\(x=\frac{11}{3}\).
The \(y\)-coordinates of the turning points are calculated
as:
\begin{align*}
f(-1) & = -(-1)^{3} + 4(-1)^{2} +11(-1) - 30 \\
& = -36
\end{align*}
and
\begin{align*}
f(\frac{11}{3}) & = -\left(\frac{11}{3}\right)^{3} +
4\left(\frac{11}{3}\right)^{2} + 11\left(\frac{11}{3}\right) -
30 \\
& = \frac{400}{3}
\end{align*}
Therefore, the turning points are: \((-1;-36)\) and
\((\frac{11}{3};\frac{400}{27})\).