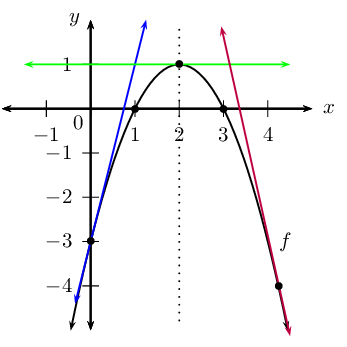
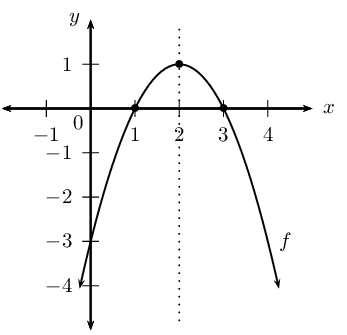
Draw a graph of \(f\), indicating all intercepts
and turning points.
Complete the square:
\begin{align*}
y&=-[x^{2}-4x+3] \\
&=-[(x-2)^{2}-4+3] \\
&=-(x-2)^{2}+1\\
\text{Turning point}:&(2;1)
\end{align*}
\(\text{Intercepts:}\\
y_{\text{int}}: x = 0, y = -3 \\
x_{\text{int}}: y=0, \\
-x^{2} +4x -3 = 0 \\
x^{2} - 4x + 3 = 0 \\
(x-3)(x-1) = 0 \\
x=3 \text{ or } x=1 \\
\text{Shape: “frown” } (a < 0) \\\)
Find the equations of the tangents to \(f\) at:
- the \(y\)-intercept of \(f\).
- the turning point of \(f\).
- the point where \(x = \text{4,25}\).
- \begin{align*}
y_{\text{int}}: (0;-3) \\
m_{\text{tangent}} = f'(x) &= -2x + 4 \\
f'(0) &=-2(0) + 4 \\
\therefore m &=4\\
\text{Tangent }y&=4x+c\\
\text{Through }(0;-3) \therefore y&=4x-3
\end{align*}
- \begin{align*}
\text{Turning point: } (2;1) \\
m_{\text{tangent}} = f'(2) &= -2(2) + 4 \\
&=0\\
\text{Tangent equation } y &= 1
\end{align*}
- \begin{align*}
\text{If } x &=\text{4,25} \\
f(\text{4,25})&=-\text{4,25}^{2}+4(\text{4,25})-3
\\
&= -\text{4,0625} \\
m_{\text{tangent}} \text{ at } x&=
\text{4,25} \\
m&=-2(\text{4,25})+4\\
&=-\text{4,5} \\
\text{Tangent }y&=-\text{4,5}x+c\\
\text{Through }(\text{4,25};-\text{4,0625}) \\
-\text{4,0625}&=-\text{4,5}(\text{4,25})+c\\
\therefore c&= \text{15,0625} \\
y&=-\text{4,5}x+\text{15,0625}
\end{align*}
Draw the three tangents above on your graph of
\(f\).
Write down all observations about the three
tangents to \(f\).
Tangent at \(y_{\text{int}}\) (blue line): gradient is
positive, the function is increasing at this point.
Tangent at turning point (green line): gradient is zero,
tangent is a horizontal line, parallel to \(x\)-axis.
Tangent at \(x=\text{4,25}\) (purple line): gradient is
negative, the function is decreasing at this point.