Determine \(\frac{g\left(x+h\right)-g\left(x\right)}{h}\).
\begin{align*} g(x)&=-x^{2}\\ g(x+h)&=-(x+h)^{2} \\ \therefore \frac{g\left(x+h\right)-g\left(x\right)}{h} &= \frac{-(x+h)^{2}-(-x^{2})}{h} \end{align*}
|
Previous
6.1 Limits
|
Next
6.3 Rules for differentiation
|
We know that the gradient of the tangent to a curve with equation \(y = f(x)\) at \(x=a\) can be determine using the formula:
\[\text{Gradient at a point } = \lim_{h\to 0}\frac{f\left(a+h\right)-f\left(a\right)}{h}\]We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent to the graph) at any point on the graph. This expression (or gradient function) is called the derivative.
The derivative of a function \(f\left(x\right)\) is written as \({f}'\left(x\right)\) and is defined by:
\[{f}'\left(x\right)=\lim_{h\to 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}\]The process of determining the derivative of a given function.
This method is called differentiation from first principles or using the definition.
Calculate the derivative of \(g\left(x\right)=2x-3\) from first principles.
The derivative \({g}'\left(x\right) = 2\).
Notation
There are a few different notations used to refer to derivatives. It is very important that you learn to identify these different ways of denoting the derivative and that you are consistent in your usage of them when answering questions.
If we use the common notation \(y=f\left(x\right)\), where the dependent variable is \(y\) and the independent variable is \(x\), then some alternative notations for the derivative are as follows:
\[{f}'\left(x\right)={y}'=\frac{dy}{dx}=\frac{df}{dx}=\frac{d}{dx}[f\left(x\right)]=Df\left(x\right)={D}_{x}y\]The symbols \(D\) and \(\frac{d}{dx}\) are called differential operators because they indicate the operation of differentiation.
\(\frac{dy}{dx}\) means \(y\) differentiated with respect to \(x\). Similarly, \(\frac{dp}{dx}\) means \(p\) differentiated with respect to \(x\).
Important: \(\frac{dy}{dx}\) is not a fraction and does not mean \(dy \div dx\).
Calculate \(\frac{dp}{dx}\) from first principles if \(p\left(x\right)= - \frac{2}{x}\).
It is sometimes easier to write the right-hand side of the equation as:
\begin{align*} \frac{dp}{dx} & = \lim_{h\to 0}\frac{1}{h} \left(\frac{-2}{x + h} + \frac{2}{x} \right) \\ & = \lim_{h\to 0} \frac{1}{h} \left(\frac{-2x + 2(x + h)}{x(x + h)} \right) \\ & = \lim_{h\to 0} \frac{1}{h} \left(\frac{-2x + 2x + 2h }{x(x + h)} \right) \\ & = \lim_{h\to 0} \frac{1}{h} \left(\frac{2h }{x^{2} + xh} \right) \\ & = \lim_{h\to 0} \frac{2}{x^{2} + xh} \\ & = \frac{2}{x^{2}} \end{align*}Notice: even though \(h\) remains in the denominator, we can take the limit since it does not result in division by \(\text{0}\).
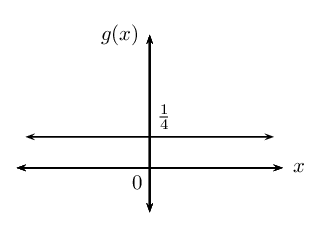
Differentiate \(g\left(x\right)= \frac{1}{4}\) from first principles and interpret the answer.
The gradient of \(g(x)\) is equal to \(\text{0}\) at any point on the graph. The derivative of this constant function is equal to \(\text{0}\).
Given: \(g\left(x\right)=-{x}^{2}\)
Determine \(\frac{g\left(x+h\right)-g\left(x\right)}{h}\).
\begin{align*} g(x)&=-x^{2}\\ g(x+h)&=-(x+h)^{2} \\ \therefore \frac{g\left(x+h\right)-g\left(x\right)}{h} &= \frac{-(x+h)^{2}-(-x^{2})}{h} \end{align*}
Hence, determine \(\displaystyle\lim_{h\to 0}\frac{g\left(x+h\right)-g\left(x\right)}{h}\).
\begin{align*} \lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h} &=\lim_{h \to 0}\dfrac{-(x+h)^{2}-(-x^{2})}{h}\\ &=\lim_{h \to 0}\dfrac{-(x^{2} + 2xh +h^{2}) + x^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{-x^{2} - 2xh -h^{2} + x^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{-2xh-h^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{h(-2x-h)}{h}\\ &=\lim_{h \to 0}-2x-h\\ &=-2x \end{align*}
Explain the meaning of your answer in (b).
The derivative of \(g(x)\) is \(g'(x) = -2x\). The gradient of the function \(g\) is given by the expression \(-2x\). The gradient of the graph depends on the value of \(x\).
Find the derivative of \(f\left(x\right)=-2{x}^{2}+3x+1\) using first principles.
\begin{align*} f(x) & = -2x^{2}+3x+1\\ f(x+h) & = -2(x+h)^{2}+3(x+h)+1\\ f'(x)&=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{h \to 0}\dfrac{-2(x+h)^{2} + 3(x+h)+1 -(-2x^{2} + 3x+1)}{h}\\ &=\lim_{h \to 0}\dfrac{-2(x^{2} + 2xh +h^{2})+1 + 3x + 3h + 2x^{2} - 3x-1}{h}\\ &=\lim_{h \to 0}\dfrac{-2x^{2} - 4xh - 2h^{2} + 3h + 2x^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{-4xh - 2h^{2} + 3h}{h}\\ &=\lim_{h \to 0}\dfrac{h(-4x - 2h + 3)}{h}\\ &=\lim_{h \to 0}(-4x-2h+3)\\ f'(x)&=-4x+3 \end{align*}
Determine the derivative of \(f\left(x\right)=\frac{1}{x-2}\) using first principles.
\begin{align*} f(x) & = \frac{1}{x-2}\\ f(x+h) & = \frac{1}{x+h-2}\\ f'(x)&=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}\\ &=\lim_{h \to 0}\dfrac{\frac{1}{x+h-2} - \frac{1}{x-2}}{h}\\ &=\lim_{h \to 0}\dfrac{\frac{(x-2)-(x+h-2)}{(x+h-2)(x-2)}}{h}\\ &=\lim_{h \to 0}\dfrac{\frac{x-2-x-h+2}{(x+h-2)(x-2)}}{h}\\ &=\lim_{h \to 0}\left(\dfrac{-h}{(x+h-2)(x-2)}\right) \times \frac{1}{h}\\ &=\lim_{h \to 0}\dfrac{-1}{(x+h-2)(x-2)}\\ f'(x)&=\frac{-1}{(x-2)^{2}} \end{align*}
Determine \({g}'\left(3\right)\) from first principles if \(g\left(x\right)=-5{x}^{2}\).
\begin{align*} g(x) & = -5x^{2}\\ g(x+h) & = -5(x+h)^{2}\\ g'(x)&=\lim_{h \to 0}\dfrac{g(x+h)-g(x)}{h} \\ &=\lim_{h \to 0}\dfrac{-5(x^{2}+2xh+h^{2}) - (-5x^{2})}{h}\\ &=\lim_{h \to 0}\dfrac{-5x^{2}-10xh-5h^{2}+5x^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{-10xh-5h^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{h(-10x-5h)}{h}\\ &=\lim_{h \to 0}(-10x-5h)\\ &=-10x \end{align*}
Therefore: \begin{align*} g'(3) & = -10(3)\\ & = -30 \end{align*}
If \(p\left(x\right)=4x(x-1)\), determine \({p}'\left(x\right)\) using first principles.
\begin{align*} p(x)&= 4x(x-1)\\ & = 4x^{2}-4x \\ p(x+h) & = 4(x+h)^{2}-4(x+h)\\ p'(x)&=\lim_{h \to 0}\dfrac{p(x+h)-p(x)}{h} \\ &=\lim_{h \to 0}\dfrac{4(x^{2}+2xh+h^{2})-4x-4h-4x^{2}+4x}{h}\\ &=\lim_{h \to 0}\dfrac{4x^{2}+8xh+4h^{2}-4h-4x^{2}}{h}\\ &=\lim_{h \to 0}\dfrac{h(8x+4h-4)}{h}\\ &=\lim_{h \to 0}(8x+4h-4)\\ &=8x-4 \end{align*}
Find the derivative of \(k\left(x\right)=10{x}^{3}\) using first principles.
\begin{align*} k(x) & = 10{x}^{3}\\ k(x+h) & = 10{(x + h)}^{3}\\ k'(x)&=\lim_{h \to 0}\dfrac{k(x+h)-k(x)}{h} \\ &=\lim_{h \to 0}\dfrac{10{(x + h)}^{3}- 10{x}^{3}}{h}\\ &=\lim_{h \to 0}\dfrac{10 \left(x^{3} + 3x^{2}h + 3xh^{2} + h^{3} \right) - 10x^{3}}{h}\\ &=\lim_{h \to 0}\dfrac{10 x^{3} + 30x^{2}h + 30xh^{2} + 10h^{3} - 10x^{3}}{h}\\ &=\lim_{h \to 0}\dfrac{ 30x^{2}h + 30xh^{2} + 10h^{3} }{h}\\ &=\lim_{h \to 0} \left( 30x^{2} + 30xh + 10h^{2} \right) \\ k'(x) &= 30x^{2} \end{align*}
Differentiate \(f(x)=x^{n}\) using first principles.
(Hint: Use Pascal's triangle)
Step 1: Use first principles to find the derivative.
\[f'(x) = \lim_{h \to 0} \text{ (average gradient)}\] \begin{align*} \text{Average gradient } &=\frac{f(x+h)-f(x)}{h} \\ &= \frac{(x+h)^{n}-x^{n}}{h} \end{align*}Expand \((x+h)^{n}\) using the pattern of the coefficients given by Pascal's Triangle:
\[\begin{array}{ccccccccccccc} x \qquad & & & & & & & 1& & & & & \\ (x+h) \qquad& & & & & &1& &1& & & & \\ (x+h)^2 \qquad & & & & & 1& & 2& & 1& & & \\ (x+h)^3 \qquad& & & &1& &3& &3& &1& & \\ (x+h)^4 \qquad& & & 1& & 4& & 6& & 4& & 1& \\ . \qquad& & & & & & & & & & & & \\ . \qquad& & & & & & & & & & & & \\ (x+h)^n \qquad& & 1& &n& .&.& .&.& .&n& & 1 \end{array}\] \[\therefore (x+h)^{n} = x^{n} + nx^{n-1}h \cdots nxh^{n-1} + h^{n}\]All the terms, except \(x^{n}\), contain \(h\).
\begin{align*} \text{Average gradient } &= \frac{(x^{n}+nx^{n-1}h+\cdots+nxh^{n-1}+h^{n})-x^{n}}{h} \\ &= \frac{nx^{n-1}h+\cdots+nxh^{n-1}+h^{n}}{h} \\ &= \frac{h(nx^{n-1}+\cdots+nxh^{n-2}+h^{n-1})}{h} \\ &= nx^{n-1} + \cdots + nxh^{n-2} + h^{n-1} \end{align*} \begin{align*} \therefore \text{Average gradient } &=\lim_{h \to 0} \left(nx^{n-1}+\cdots+nxh^{n-2}+h^{n-1}\right) \\ \therefore &= nx^{n-1} \end{align*} \begin{align*} \text{If } f(x) &= x^{n} \\ f'(x) &= nx^{n-1} \end{align*}This is a very valuable general rule for finding the derivative of a function.
|
Previous
6.1 Limits
|
Table of Contents |
Next
6.3 Rules for differentiation
|