6.4 Trigonometric equations | Trigonometry

6.4 Trigonometric equations (EMBHM)

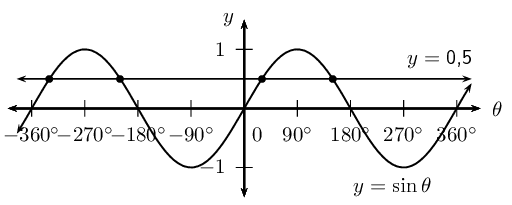
Solving trigonometric equations requires that we find the value of the angles that satisfy the equation. If a specific interval for the solution is given, then we need only find the value of the angles within the given interval that satisfy the equation. If no interval is given, then we need to find the general solution. The periodic nature of trigonometric functions means that there are many values that satisfy a given equation, as shown in the diagram below.

Worked example 12: Solving trigonometric equations

Solve for \(\theta\) (correct to one decimal place), given \(\tan \theta = 5\) and \(\theta \in [\text{0}\text{°};\text{360}\text{°}]\).

Use a calculator to solve for \(\theta\)

\begin{align*} \tan \theta &= 5 \\ \therefore \theta &= \tan^{-1}5 \\ &= \text{78,7}\text{°} \end{align*}

This value of \(\theta\) is an acute angle which lies in the first quadrant and is called the reference angle.

Use the CAST diagram to determine in which quadrants \(\tan \theta\) is positive

The CAST diagram indicates that \(\tan \theta\) is positive in the first and third quadrants, therefore we must determine the value of \(\theta\) such that \(\text{180}\text{°} < \theta < \text{270}\text{°}\).

Using reduction formulae, we know that \(\tan (\text{180}\text{°} + \theta) = \tan \theta\)

\begin{align*} \theta &= \text{180}\text{°} + \text{78,7}\text{°} \\ \therefore \theta &= \text{258,7}\text{°} \end{align*}

Use a calculator to check that the solution satisfies the original equation

Write the final answer

\(\theta = \text{78,7}\text{°}\) or \(\theta = \text{258,7}\text{°}\).

Worked example 13: Solving trigonometric equations

Solve for \(\alpha\) (correct to one decimal place), given \(\cos \alpha = -\text{0,7}\) and \(\theta \in [\text{0}\text{°};\text{360}\text{°}]\).

Use a calculator to find the reference angle

To determine the reference angle, we do not include the negative sign. The reference angle must be an acute angle in the first quadrant, where all the trigonometric functions are positive.

\begin{align*} \text{ref } \angle &= \cos^{-1}\text{0,7} \\ &= \text{45,6}\text{°} \end{align*}

Use the CAST diagram to determine in which quadrants \(\cos \alpha\) is negative

The CAST diagram indicates that \(\cos \alpha\) is negative in the second and third quadrants, therefore we must determine the value of \(\alpha\) such that \(\text{90}\text{°} < \alpha < \text{270}\text{°}\).

Using reduction formulae, we know that \(\cos (\text{180}\text{°} - \alpha) = -\cos \alpha\) and \(\cos (\text{180}\text{°} + \alpha) = -\cos \alpha\)

In the second quadrant:

\begin{align*} \alpha &= \text{180}\text{°} - \text{45,6}\text{°} \\ &= \text{134,4}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \alpha &= \text{180}\text{°} + \text{45,6}\text{°} \\ &= \text{225,6}\text{°} \end{align*}

Note: the reference angle \((\text{45,6}\text{°})\) does not form part of the solution.

Use a calculator to check that the solution satisfies the original equation

Write the final answer

\(\alpha = \text{134,4}\text{°}\) or \(\alpha = \text{225,6}\text{°}\).

Worked example 14: Solving trigonometric equations

Solve for \(\beta\) (correct to one decimal place), given \(\sin \beta = -\text{0,5}\) and \(\beta \in [-\text{360}\text{°};\text{360}\text{°}]\).

Use a calculator to find the reference angle

To determine the reference angle, we use a positive value.

\begin{align*} \text{ref } \angle &= \sin^{-1}\text{0,5} \\ &= \text{30}\text{°} \end{align*}

Use the CAST diagram to determine in which quadrants \(\sin \beta\) is negative

The CAST diagram indicates that \(\sin \beta\) is negative in the third and fourth quadrants. We also need to find the values of \(\beta\) such that \(-\text{360}\text{°} \leq \beta \leq \text{360}\text{°}\).

Using reduction formulae, we know that \(\sin (\text{180}\text{°} + \beta) = - \sin \beta\) and \(\sin (\text{360}\text{°} - \beta) = - \sin \beta\)

In the third quadrant:

\begin{align*} \beta &= \text{180}\text{°} + \text{30}\text{°} \\ &= \text{210}\text{°} \\ \text{or } \beta &= -\text{180}\text{°} + \text{30}\text{°} \\ &= -\text{150}\text{°} \end{align*}

In the fourth quadrant:

\begin{align*} \beta &= \text{360}\text{°} - \text{30}\text{°} \\ &= \text{330}\text{°} \\ \text{or } \beta &= \text{0}\text{°} - \text{30}\text{°} \\ &= -\text{30}\text{°} \end{align*}

Notice: the reference angle \((\text{30}\text{°})\) does not form part of the solution.

Use a calculator to check that the solution satisfies the original equation

Write the final answer

\(\beta = -\text{150}\text{°}\), \(-\text{30}\)\(\text{°}\), \(\text{210}\)\(\text{°}\) or \(\text{330}\)\(\text{°}\).

Solving trigonometric equations

Textbook Exercise 6.7

\(4 \cos \alpha = 2\)

\begin{align*} 4 \cos \alpha &= 2 \\ \cos \alpha &= \frac{1}{2} \\ \text{ref } \angle &= \cos^{-1}\text{0,5} \\ &= \text{60}\text{°} \\ \therefore \alpha &= \text{60}\text{°} \end{align*}

In the fourth quadrant:

\begin{align*} \alpha &= \text{360}\text{°} - \text{60}\text{°} \\ &= \text{300}\text{°} \end{align*}

\(\alpha = \text{60}\text{°}; \text{300}\text{°}\)

\(\sin \alpha + \text{3,65} = 3\)

\begin{align*} \sin \alpha + \text{3,65} &= 3\\ \sin \alpha &= -\text{0,65} \\ \text{ref } \angle &= \sin^{-1}\text{0,65} \\ &= \text{40,5}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \alpha &= \text{180}\text{°} + \text{40,5}\text{°} \\ &= \text{220,5}\text{°} \end{align*}

In the fourth quadrant:

\begin{align*} \alpha &= \text{360}\text{°} - \text{40,5}\text{°} \\ &= \text{319,5}\text{°} \end{align*}

\(\alpha = \text{220,5}\text{°}; \text{319,5}\text{°}\)

\(\tan \alpha = 5\frac{1}{4}\)

\begin{align*} \tan \alpha &= 5\frac{1}{4} \\ \tan \alpha &= -\text{5,25} \\ \text{ref } \angle &= \tan^{-1}\text{5,25} \\ &= \text{79,2}\text{°} \\ \therefore \alpha &= \text{79,2}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \alpha &= \text{180}\text{°} + \text{79,2}\text{°} \\ &= \text{259,2}\text{°} \end{align*}

\(\alpha = \text{79,2}\text{°}; \text{259,2}\text{°}\)

\(\cos \alpha + \text{0,939} = 0\)

\begin{align*} \cos \alpha + \text{0,939} &= 0\\ \cos \alpha &= -\text{0,939} \\ \text{ref } \angle &= \cos^{-1}\text{0,939} \\ &= \text{20,1}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \alpha &= \text{180}\text{°} + \text{20,1}\text{°} \\ &= \text{200,1}\text{°} \end{align*}

In the fourth quadrant:

\begin{align*} \alpha &= \text{360}\text{°} - \text{20,1}\text{°} \\ &= \text{339,9}\text{°} \end{align*}

\(\alpha = \text{200,1}\text{°}; \text{339,9}\text{°}\)

\(5 \sin \alpha = 3\)

\begin{align*} 5 \sin \alpha &= 3\\ \sin \alpha &= \frac{3}{5}\\ \text{ref } \angle &= \sin^{-1} \left( \frac{3}{5} \right) \\ &= \text{36,9}\text{°} \\ \therefore \alpha &= \text{36,9}\text{°} \end{align*}

In the second quadrant:

\begin{align*} \alpha &= \text{180}\text{°} - \text{20,1}\text{°} \\ &= \text{143,1}\text{°} \end{align*}

\(\alpha = \text{36,9}\text{°}; \text{143,1}\text{°}\)

\(\frac{1}{2} \tan \alpha = -\text{1,4}\)

\begin{align*} \frac{1}{2} \tan \alpha &= -\text{1,4} \\ \tan \alpha &= -\text{2,8} \\ \text{ref } \angle &= \tan^{-1}\text{2,8} \\ &= \text{70,3}\text{°} \end{align*}

In the second quadrant:

\begin{align*} \alpha &= \text{180}\text{°} - \text{70,3}\text{°} \\ &= \text{109,7}\text{°} \end{align*}

In the fourth quadrant:

\begin{align*} \alpha &= \text{360}\text{°} - \text{70,3}\text{°} \\ &= \text{289,7}\text{°} \end{align*}

\(\alpha = \text{109,7}\text{°}; \text{289,7}\text{°}\)

\(\sin \theta = \text{0,6}\)

\begin{align*} \sin \theta &= \text{0,6} \\ \text{ref } \angle &= \sin^{-1}\text{0,6} \\ &= \text{36,9}\text{°} \\ \therefore \theta &= \text{36,9}\text{°} \end{align*}

In the second quadrant:

\begin{align*} \theta &= \text{180}\text{°} - \text{36,9}\text{°} \\ &= \text{143,1}\text{°} \end{align*}

Negative angles:

\begin{align*} \theta &= \text{36,9}\text{°} - \text{360}\text{°} \\ &= -\text{323,1}\text{°} \\ \text{And } \theta &= \text{143,1}\text{°} - \text{360}\text{°} \\ &= -\text{216,9}\text{°} \end{align*}

\(\theta = -\text{323,1}\text{°}; -\text{216,9}\text{°}; \text{36,9}\text{°}; \text{143,1}\text{°}\)

\(\cos \theta + \frac{3}{4} = 0\)

\begin{align*} \cos \theta + \frac{3}{4} &= 0 \\ \cos \theta &= - \frac{3}{4} \\ \text{ref } \angle &= \cos^{-1} \left( \frac{3}{4} \right) \\ &= \text{41,4}\text{°} \end{align*}

In the second quadrant:

\begin{align*} \theta &= \text{180}\text{°} - \text{41,4}\text{°} \\ &= \text{138,6}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \theta &= \text{180}\text{°} + \text{41,4}\text{°} \\ &= \text{221,4}\text{°} \end{align*}

Negative angles:

\begin{align*} \theta &= \text{138,6}\text{°} - \text{360}\text{°} \\ &= -\text{221,4}\text{°} \\ \text{And } \theta &= \text{221,4}\text{°} - \text{360}\text{°} \\ &= -\text{138,6}\text{°} \end{align*}

\(\theta = -\text{221,4}\text{°}; -\text{138,6}\text{°}; \text{138,6}\text{°}; \text{221,4}\text{°}\)

\(3 \tan \theta = 20\)

\begin{align*} 3 \tan \theta &= 20 \\ \tan \theta &= \frac{20}{3} \\ \text{ref } \angle &= \tan^{-1} \left( \frac{20}{3} \right) \\ &= \text{81,5}\text{°} \\ \theta &= \text{81,5}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \theta &= \text{180}\text{°} + \text{81,5}\text{°} \\ &= \text{261,5}\text{°} \end{align*}

Negative angles:

\begin{align*} \theta &= \text{81,5}\text{°} - \text{360}\text{°} \\ &= -\text{278,5}\text{°} \\ \text{And } \theta &= \text{261,5}\text{°} - \text{360}\text{°} \\ &= -\text{98,5}\text{°} \end{align*}

\(\theta = -\text{278,5}\text{°}; -\text{98,5}\text{°}; \text{81,5}\text{°}; \text{261,5}\text{°}\)

\(\sin \theta = \cos \text{180}\text{°}\)

\begin{align*} \sin \theta &= \cos \text{180}\text{°} \\ \sin \theta &= -1 \\ \text{ref } \angle &= \sin^{-1} \left( 1 \right) \\ &= \text{90}\text{°} \end{align*}

In the third quadrant:

\begin{align*} \theta &= \text{180}\text{°} + \text{90}\text{°} \\ &= \text{270}\text{°} \end{align*}

Negative angles:

\begin{align*} \theta &= \text{270}\text{°} - \text{360}\text{°} \\ &= -\text{90}\text{°} \end{align*}

\(\theta = -\text{90}\text{°}; \text{270}\text{°}\)

\(2 \cos \theta = \frac{4}{5}\)

\begin{align*} 2 \cos \theta &= \frac{4}{5}\\ \cos \theta &= \frac{2}{5} \\ \text{ref } \angle &= \cos^{-1} \left( \frac{2}{5} \right) \\ &= \text{66,4}\text{°} \\ \theta &= \text{66,4}\text{°} \end{align*}

In the fourth quadrant:

\begin{align*} \theta &= \text{360}\text{°} - \text{66,4}\text{°} \\ &= \text{293,6}\text{°} \end{align*}

Negative angles:

\begin{align*} \theta &= \text{66,4}\text{°} - \text{360}\text{°} \\ &= -\text{293,6}\text{°} \\ \text{And } \theta &= \text{293,6}\text{°} - \text{360}\text{°} \\ &= -\text{66,4}\text{°} \end{align*}

\(\theta = -\text{293,6}\text{°}; -\text{66,4}\text{°}; \text{66,4}\text{°}; \text{293,6}\text{°}\)

The general solution (EMBHN)

In the previous worked example, the solution was restricted to a certain interval. However, the periodicity of the trigonometric functions means that there are an infinite number of positive and negative angles that satisfy an equation. If we do not restrict the solution, then we need to determine the general solution to the equation. We know that the sine and cosine functions have a period of \(\text{360}\)\(\text{°}\) and the tangent function has a period of \(\text{180}\)\(\text{°}\).

Method for finding the general solution:

Determine the reference angle (use a positive value).
Use the CAST diagram to determine where the function is positive or negative (depending on the given equation).
Find the angles in the interval \([\text{0}\text{°}; \text{360}\text{°}]\) that satisfy the equation and add multiples of the period to each answer.
Check answers using a calculator.

Worked example 15: Finding the general solution

Determine the general solution for \(\sin \theta = \text{0,3}\) (give answers correct to one decimal place).

Use a calculator to find the reference angle

\begin{align*} \sin \theta &= \text{0,3} \\ \therefore \text{ref } \angle &= \sin^{-1}\text{0,3} \\ &= \text{17,5}\text{°} \end{align*}

Use CAST diagram to determine in which quadrants \(\sin \theta\) is positive

The CAST diagram indicates that \(\sin \theta\) is positive in the first and second quadrants.

Using reduction formulae, we know that \(\sin (\text{180}\text{°} - \theta) = \sin \theta\).

In the first quadrant:

\begin{align*} \theta &= \text{17,5}\text{°} \\ \therefore \theta &= \text{17,5}\text{°} + k \cdot \text{360}\text{°} \end{align*}

In the second quadrant:

\begin{align*} \theta &= \text{180}\text{°} - \text{17,5}\text{°} \\ \therefore \theta &= \text{162,5}\text{°} + k \cdot \text{360}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Check that the solution satisfies the original equation

We can select random values of \(k\) to check that the answers satisfy the original equation.

Let \(k = 4\):

\begin{align*} \theta &= \text{17,5}\text{°} + 4(\text{360})° \\ \therefore \theta &= \text{1 457,5}\text{°} \\ \text{And } \sin \text{1 457,5}\text{°} &= \text{0,3007} \ldots \end{align*}

This solution is correct.

Similarly, if we let \(k = -2\):

\begin{align*} \theta &= \text{162,5}\text{°} - 2(\text{360})° \\ \therefore \theta &= -\text{557,5}\text{°} \\ \text{And } \sin (-\text{557,5}\text{°}) &= \text{0,3007} \ldots \end{align*}

This solution is also correct.

Write the final answer

\(\theta = \text{17,5}\text{°} + k \cdot \text{360}\text{°}\) or \(\theta = \text{162,5}\text{°} + k \cdot \text{360}\text{°}\).

Worked example 16: Finding the general solution

Determine the general solution for \(\cos 2\theta = - \text{0,6427}\) (give answers correct to one decimal place).

Use a calculator to find the reference angle

\begin{align*} \text{ref } \angle &= \sin^{-1}\text{0,6427} \\ &= \text{50,0}\text{°} \end{align*}

Use CAST diagram to determine in which quadrants \(\cos \theta\) is negative

The CAST diagram shows that \(\cos \theta\) is negative in the second and third quadrants.

Therefore we use the reduction formulae \(\cos (\text{180}\text{°} - \theta) = - \cos \theta\) and \(\cos (\text{180}\text{°} + \theta) = - \cos \theta\).

In the second quadrant:

\begin{align*} 2\theta &= \text{180}\text{°} - \text{50}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{130}\text{°} + k \cdot \text{360}\text{°} \\ \therefore \theta &= \text{65}\text{°} + k \cdot \text{180}\text{°} \end{align*}

In the third quadrant:

\begin{align*} 2\theta &= \text{180}\text{°} + \text{50}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{230}\text{°} + k \cdot \text{360}\text{°} \\ \therefore \theta &= \text{115}\text{°} + k \cdot \text{180}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Remember: also divide the period \((\text{360}\text{°})\) by the coefficient of \(\theta\).

Check that the solution satisfies the original equation

We can select random values of \(k\) to check that the answers satisfy the original equation.

Let \(k = 2\):

\begin{align*} \theta &= \text{65}\text{°} + 2(\text{180}\text{°}) \\ \therefore \theta &= \text{425}\text{°} \\ \text{And } \cos 2(\text{425})° &= -\text{0,6427} \ldots \end{align*}

This solution is correct.

Similarly, if we let \(k = -5\):

\begin{align*} \theta &= \text{115}\text{°} - 5(\text{180}\text{°})\\ \therefore \theta &= -\text{785}\text{°} \\ \text{And } \cos 2(-\text{785}\text{°}) &= -\text{0,6427} \ldots \end{align*}

This solution is also correct.

Write the final answer

\(\theta = \text{65}\text{°} + k \cdot \text{180}\text{°}\) or \(\theta = \text{115}\text{°} + k \cdot \text{180}\text{°}\).

Worked example 17: Finding the general solution

Determine the general solution for \(\tan (2\alpha - \text{10}\text{°}) = \text{2,5}\) such that \(-\text{180}\text{°} \leq \alpha \leq \text{180}\text{°}\) (give answers correct to one decimal place).

Make a substitution

To solve this equation, it can be useful to make a substitution: let \(x = 2\alpha - \text{10}\text{°}\).

\[\tan (x) = \text{2,5}\]

Use a calculator to find the reference angle

\begin{align*} \tan x &= \text{2,5} \\ \therefore \text{ref } \angle &= \tan^{-1} \text{2,5} \\ &= \text{68,2}\text{°} \end{align*}

Use CAST diagram to determine in which quadrants the tangent function is positive

We see that \(\tan x\) is positive in the first and third quadrants, so we use the reduction formula \(\tan (\text{180}\text{°} + x) = \tan x\). It is also important to remember that the period of the tangent function is \(\text{180}\)\(\text{°}\).

In the first quadrant:

\begin{align*} x &= \text{68,2}\text{°} + k \cdot \text{180}\text{°} \\ \text{Substitute } x &= 2 \alpha -\text{10}\text{°} \\ 2 \alpha -\text{10}\text{°} &= \text{68,2}\text{°} + k \cdot \text{180}\text{°} \\ 2 \alpha &= \text{78,2}\text{°} + k \cdot \text{180}\text{°} \\ \therefore \alpha &= \text{39,1}\text{°} + k \cdot \text{90}\text{°} \end{align*}

In the third quadrant:

\begin{align*} x &= \text{180}\text{°} + \text{68,2}\text{°} + k \cdot \text{180}\text{°} \\ &= \text{248,2}\text{°} + k \cdot \text{180}\text{°} \\ \text{Substitute } x &= 2 \alpha -\text{10}\text{°} \\ 2 \alpha -\text{10}\text{°} &= \text{248,2}\text{°} + k \cdot \text{180}\text{°} \\ 2 \alpha &= \text{258,2}\text{°} + k \cdot \text{180}\text{°} \\ \therefore \alpha &= \text{129,1}\text{°} + k \cdot \text{90}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Remember: to divide the period \((\text{180}\text{°})\) by the coefficient of \(\alpha\).

Find the answers within the given interval

Substitute suitable values of \(k\) to determine the values of \(\alpha\) that lie within the interval (\(-\text{180}\text{°} \leq \alpha \leq \text{180}\text{°}\)).

	I: \(\alpha = \text{39,1}\text{°} + k \cdot \text{90}\text{°}\)		III: \(\alpha = \text{129,1}\text{°} + k \cdot \text{90}\text{°}\)
\(k = 0\)	\(\text{39,1}\)\(\text{°}\)		\(\text{129,1}\)\(\text{°}\)
\(k = 1\)	\(\text{129,1}\)\(\text{°}\)		\(\text{219,1}\)\(\text{°}\)	(outside)
\(k = 2\)	\(\text{219,1}\)\(\text{°}\)	(outside)
\(k = -1\)	\(-\text{50,9}\)\(\text{°}\)		\(\text{39,1}\)\(\text{°}\)
\(k = -2\)	\(-\text{140,9}\)\(\text{°}\)		\(-\text{50,9}\)\(\text{°}\)
\(k = -3\)	\(-\text{230,9}\)\(\text{°}\)	(outside)	\(-\text{140,9}\)\(\text{°}\)
\(k = -4\)			\(-\text{230,9}\)\(\text{°}\)	(outside)

Notice how some of the values repeat. This is because of the periodic nature of the tangent function. Therefore we need only determine the solution:

\[\alpha = \text{39,1}\text{°} + k \cdot \text{90}\text{°}\] for \(k \in \mathbb{Z}\).

Write the final answer

\(\alpha = -\text{140,9}\text{°}\); \(-\text{50,9}\)\(\text{°}\); \(\text{39,1}\)\(\text{°}\) or \(\text{129,1}\)\(\text{°}\).

Worked example 18: Finding the general solution using co-functions

Determine the general solution for \(\sin (\theta - \text{20}\text{°}) = \cos 2\theta\).

Use the CAST diagram to decide on the quadrants

\begin{align*} \sin(\theta - \text{20}\text{°}) &= \cos2\theta \\ \sin(\theta - \text{20}\text{°}) &= \sin(\text{90}\text{°} - 2\theta) \end{align*}

The right hand side of the equation is positive, and the sine function is positive in the first and second quadrants. Therefore, we will reduce the equation as if the solution were in the first and second quadrants (using the angle and \(\text{180}\text{°}\) minus the angle).

Solve the equation

\begin{align*} \sin(\theta - \text{20}\text{°}) &= \cos2\theta \\ \sin(\theta - \text{20}\text{°}) &= \sin(\text{90}\text{°} - 2\theta) \end{align*}

Solution 1:

\begin{align*} \theta - \text{20}\text{°} &= \text{90}\text{°} - 2\theta + k \cdot \text{360}\text{°} \\ 3\theta &= \text{110}\text{°} + k \cdot \text{360}\text{°} \\ \therefore \theta &= \text{36,67}\text{°} + k \cdot \text{120}\text{°} \end{align*}

Solution 2:

\begin{align*} \theta - \text{20}\text{°} &= \text{180}\text{°} - (\text{90}\text{°} - 2\theta) + k \cdot \text{360}\text{°} \\ \theta - \text{20}\text{°} &= \text{180}\text{°} - \text{90}\text{°} + 2\theta + k \cdot \text{360}\text{°} \\ -\theta &= \text{110}\text{°} + k \cdot \text{360}\text{°}\\ \theta &= -\text{110}\text{°} + k \cdot \text{360}\text{°} \\ \theta &= \text{250}\text{°} + k \cdot \text{360}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Check that the solution satisfies the original equation

For the first solution:

\begin{align*} \sin(\theta - \text{20}\text{°}) &= \sin(\text{36,67}\text{°} - \text{20}\text{°}) \\ &= \text{0,29} \end{align*}

and

\begin{align*} \cos2\theta &= \cos(2 \times \text{36,67}\text{°}) \\ &= \text{0,29} \end{align*}

For the second solution:

\begin{align*} \sin(\theta - \text{20}\text{°}) &= \sin(\text{250}\text{°} - \text{20}\text{°}) \\ &= -\text{0,77} \end{align*}

and

\begin{align*} \cos2\theta &= \cos(2 \times \text{250}\text{°}) \\ &= -\text{0,77} \end{align*}

Write the final answer

\(\theta = \text{36,67}\text{°} + k \cdot \text{120}\text{°}\) or \(\theta = \text{250}\text{°} + k \cdot \text{360}\text{°}, \quad k \in \mathbb{Z}\)

General solution

Textbook Exercise 6.8

Find the general solution for each equation.
Hence, find all the solutions in the interval \([-\text{180}\text{°};\text{180}\text{°}]\).

\(\cos (\theta + \text{25}\text{°}) = \text{0,231}\)

\begin{align*} \cos(\theta+\text{25}\text{°})&=\text{0,231} \\ \text{ref } \angle &= \text{76,64}\text{°} \\ \text{I quad: } \quad \theta+\text{25}\text{°}&= \text{76,64}\text{°}+ n \cdot \text{360}\text{°}, n \in \mathbb{Z}\\ \therefore \theta &= \text{51,64}\text{°} + n \cdot \text{360}\text{°} \\ \therefore \theta &=-\text{128,36}\text{°}; \text{51,64}\text{°} \\ \text{IV quad: } \quad \theta+\text{25}\text{°}&= \text{360}\text{°} - \text{76,64}\text{°} + n \cdot \text{360}\text{°}, n \in \mathbb{Z}\\ \therefore \theta &= \text{258,36}\text{°} + n \cdot \text{360}\text{°} \\ \therefore \theta &= -\text{101,64}\text{°} \end{align*}

\(\theta = -\text{128,36}\text{°}; -\text{101,64}\text{°}; \text{51,64}\text{°}\)

\(\sin 2\alpha = -\text{0,327}\)

\begin{align*} \sin2\alpha&=-\text{0,327} \\ \text{ref } \angle &= \text{19,09}\text{°} \\ \text{III quad: } \quad 2\alpha&=\text{180}\text{°} + \text{19,09}\text{°}+ n \cdot \text{360}\text{°}, n \in \mathbb{Z}\\ 2\alpha&=\text{199,09}\text{°}+ n \cdot \text{360}\text{°} \\ \therefore \alpha&=\text{99,55}\text{°}+ n \cdot \text{180}\text{°}\\ \therefore \alpha&=-\text{80,45}\text{°}; \text{99,55}\text{°} \\ \text{IV quad: } \quad 2\alpha&=\text{360}\text{°} - \text{19,09}\text{°}+ n \cdot \text{360}\text{°}, n \in \mathbb{Z} \\ 2\alpha&=\text{340,91}\text{°}+ n \cdot \text{360}\text{°} \\ \therefore \alpha&=\text{170,46}\text{°}+ n \cdot \text{180}\text{°} \\ \therefore \alpha&=-\text{9,54}\text{°}; \text{170,46}\text{°} \end{align*}

\(\theta = -\text{80,45}\text{°}; -\text{9,54}\text{°}; \text{99,55}\text{°}; \text{170,46}\text{°}\)

\(2 \tan \beta = -\text{2,68}\)

\begin{align*} 2\tan\theta&=-\text{2,68} \\ \tan\theta&=-\text{1,34} \\ \text{ref } \angle &= \text{53,27}\text{°} \\ \text{II quad: } \quad \theta &= \text{180}\text{°}- \text{53,27}\text{°}+ n \cdot \text{180}\text{°} , n \in \mathbb{Z} \\ \therefore \theta &=\text{126,73}\text{°}+ n \cdot \text{180}\text{°} \\ \therefore \theta&=-\text{53,27}\text{°}; \text{126,73}\text{°} \end{align*}

\(\theta = -\text{53,27}\text{°}; \text{126,73}\text{°}\)

\(\cos \alpha = 1\)

\begin{align*} \cos \alpha &= 1\\ \text{ref } \angle &= \text{0}\text{°} \\ \text{I/IV quad: } \quad \alpha &= \text{0}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \alpha &= \text{0}\text{°} \end{align*}

\(\alpha = \text{0}\text{°}\)

\(4 \sin \theta = 0\)

\begin{align*} 4 \sin \theta &= 0 \\ \text{ref } \angle &= \text{0}\text{°} \\ \text{I quad: } \quad \theta &= \text{0}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \text{II quad: } \quad \theta &= \text{180}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \end{align*}

\(\theta = -\text{180}\text{°}; \text{0}\text{°}; \text{180}\text{°}\)

\(\cos \theta = -1\)

\begin{align*} \cos \theta &= -1 \\ \text{ref } \angle &= \text{0}\text{°} \\ \text{I/III quad: } \quad \theta &= \text{180}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \end{align*}

\(\theta = -\text{180}\text{°}; \text{180}\text{°}\)

\(\tan \frac{\theta}{2} = \text{0,9}\)

\begin{align*} \tan \frac{\theta}{2} &= \text{0,9} \\ \text{ref } \angle &= \text{42}\text{°} \\ \text{I quad: } \quad \frac{\theta}{2} &= \text{42}\text{°}+ n \cdot \text{180}\text{°}, n \in \mathbb{Z}\\ \theta &= \text{84}\text{°}+ n \cdot \text{360}\text{°} \\ \text{III quad: } \quad \frac{\theta}{2} &= \text{180}\text{°} + \text{42}\text{°}+ n \cdot \text{180}\text{°}, n \in \mathbb{Z} \\ \frac{\theta}{2} &= \text{222}\text{°}+ n \cdot \text{180}\text{°} \\ \therefore \theta &= \text{444}\text{°}+ n \cdot \text{360}\text{°} \end{align*} \(\theta = \text{84}\text{°}\)

\(4 \cos \theta +3 = 1\)

\begin{align*} 4 \cos \theta +3 &= 1 \\ 4 \cos \theta &= - 2 \\ \cos \theta &= -\frac{1}{2} \\ \text{ref } \angle &= \text{60}\text{°} \\ \text{II quad: } \quad \theta &= \text{180}\text{°}- \text{60}\text{°}+ n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \theta &=\text{120}\text{°}+ n \cdot \text{360}\text{°} \\ \text{III quad: } \quad \theta &= \text{180}\text{°} + \text{60}\text{°}+ n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \theta &= \text{240}\text{°}+ n \cdot \text{360}\text{°} \end{align*}

\(\theta = -\text{120}\text{°}; \text{120}\text{°}\)

\(\sin 2\theta = -\frac{\sqrt{3}}{2}\)

\begin{align*} \sin 2\theta &= -\frac{\sqrt{3}}{2} \\ \text{ref } \angle &= \text{60}\text{°} \\ \text{III quad: } \quad 2\theta &= \text{180}\text{°}+ \text{60}\text{°}+ n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ 2\theta &= \text{240}\text{°}+ n \cdot \text{360}\text{°} \\ \therefore \theta &=\text{120}\text{°}+ n \cdot \text{180}\text{°} \\ \text{IV quad: } \quad \theta &= \text{360}\text{°} - \text{60}\text{°}+ n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ 2\theta &= \text{300}\text{°}+ n \cdot \text{360}\text{°} \\ \therefore \theta &= \text{150}\text{°}+ n \cdot \text{180}\text{°} \end{align*}

\(\theta = -\text{60}\text{°}; -\text{30}\text{°}; \text{120}\text{°}; \text{150}\text{°}\)

\(\cos (\theta + \text{20}\text{°}) = 0\)

\begin{align*} \cos (\theta + \text{20}\text{°}) &= 0 \\ \text{ref } \angle &= \text{0}\text{°} \\ \therefore \theta + \text{20}\text{°} &= \text{0}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \theta &= - \text{20}\text{°} + n \cdot \text{360}\text{°} \end{align*}

\(\theta = - \text{20}\text{°} + n \cdot \text{360}\text{°}\)

\(\sin 3\alpha = -1\)

\begin{align*} \sin 3\alpha &= -1 \\ \text{ref } \angle &= \text{90}\text{°} \\ \therefore 3\alpha &= \text{90}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \alpha &= \text{30}\text{°} + n \cdot \text{120}\text{°} \end{align*}

\(\alpha = \text{30}\text{°} + n \cdot \text{120}\text{°}\)

\(\tan 4\beta = \text{0,866}\)

\begin{align*} \tan 4\beta = \text{0,866} \\ \text{ref } \angle &= \text{41}\text{°} \\ \therefore 4\beta &= \text{41}\text{°} + n \cdot \text{180}\text{°} , n \in \mathbb{Z} \\ \therefore \beta &= \text{10,25}\text{°} + n \cdot \text{45}\text{°} \\ \text{III quad: } \quad 4\beta &= \text{180}\text{°} + \text{41}\text{°} + n \cdot \text{180}\text{°} , n \in \mathbb{Z} \\ &= \text{221}\text{°}+ n \cdot \text{180}\text{°} \\ \therefore \beta &= \text{55,25}\text{°} + n \cdot \text{45}\text{°} \end{align*}

\(\beta = \text{10,25}\text{°} + n \cdot \text{45}\text{°} \text{ or }\beta = \text{55,25}\text{°} + n \cdot \text{45}\text{°}\)

\(\cos (\alpha - \text{25}\text{°}) = \text{0,707}\)

\begin{align*} \cos (\alpha - \text{25}\text{°}) &= \text{0,707} \\ \text{ref } \angle &= \text{45}\text{°} \\ \therefore \alpha - \text{25}\text{°} &= \text{45}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \alpha &= \text{70}\text{°} + n \cdot \text{360}\text{°} \\ \text{IV quad: } \alpha - \text{25}\text{°} &= \text{360}\text{°} - \text{45}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ &= \text{340}\text{°}+ n \cdot \text{360}\text{°} \end{align*}

\(\alpha = \text{70}\text{°} + n \cdot \text{360}\text{°} \text{ or }\alpha = \text{340}\text{°} + n \cdot \text{360}\text{°}\)

\(2 \sin \frac{3\theta}{2} = -1\)

\begin{align*} 2 \sin \frac{3\theta}{2} &= -1 \\ \text{ref } \angle &= \text{30}\text{°} \\ \text{III quad: } \quad \frac{3\theta}{2} &= \text{180}\text{°} + \text{30}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \theta &= \frac{2}{3} \left( \text{210}\text{°} + \times n \cdot \text{360}\text{°} \right) \\ &= \text{140}\text{°} + n \cdot \text{240}\text{°} \\ \text{IV quad: } \quad \frac{3\theta}{2} &= \text{360}\text{°} - \text{30}\text{°} + n \cdot \text{360}\text{°} , n \in \mathbb{Z} \\ \therefore \theta &= \frac{2}{3} \left( \text{330}\text{°}+ n \cdot \text{360}\text{°} \right) \\ &= \text{220}\text{°} + n \cdot \text{240}\text{°} \end{align*}

\(\theta = \text{140}\text{°} + n \cdot \text{240}\text{°} \text{ or }\theta = \text{220}\text{°} + n \cdot \text{240}\text{°}\)

\(5 \tan (\beta + \text{15}\text{°}) = \frac{5}{\sqrt{3}}\)

\begin{align*} 5 \tan (\beta + \text{15}\text{°}) &= \frac{5}{\sqrt{3}} \\ \tan (\beta + \text{15}\text{°}) &= \frac{1}{\sqrt{3}} \\ \text{ref } \angle &= \text{30}\text{°}\\ \therefore \beta + \text{15}\text{°} &= \text{30}\text{°} \\ \therefore \beta &= \text{15}\text{°} + n \cdot \text{180}\text{°} \end{align*}

Solving quadratic trigonometric equations

We can use our knowledge of algebraic equations to solve quadratic trigonometric equations.

Worked example 19: Quadratic trigonometric equations

Find the general solution of \(4 \sin^2 \theta = 3\).

Simplify the equation and determine the reference angle

\begin{align*} 4 \sin^2 \theta &= 3 \\ \sin^2 \theta &= \frac{3}{4} \\ \therefore \sin \theta &= \pm\sqrt{\frac{3}{4}} \\ &= \pm \frac{\sqrt{3}}{2} \\ \therefore \text{ref } \angle &= \text{60}\text{°} \end{align*}

Determine in which quadrants the sine function is positive and negative

The CAST diagram shows that \(\sin \theta\) is positive in the first and second quadrants and negative in the third and fourth quadrants.

Positive in the first and second quadrants:

\begin{align*} \theta &= \text{60}\text{°} + k \cdot \text{360}\text{°} \\ \text{or } \theta &= \text{180}\text{°} - \text{60}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{120}\text{°} + k \cdot \text{360}\text{°} \end{align*}

Negative in the third and fourth quadrants:

\begin{align*} \theta &= \text{180}\text{°} + \text{60}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{240}\text{°} + k \cdot \text{360}\text{°} \\ \text{or } \theta &= \text{360}\text{°} - \text{60}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{300}\text{°} + k \cdot \text{360}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Check that the solution satisfies the original equation

Write the final answer

\(\theta = \text{60}\text{°} + k \cdot \text{360}\text{°}\) or \(\text{120}\text{°} + k \cdot \text{360}\text{°}\) or \(\text{240}\text{°} + k \cdot \text{360}\text{°}\) or \(\text{300}\text{°} + k \cdot \text{360}\text{°}\)

Worked example 20: Quadratic trigonometric equations

Find \(\theta\) if \(2 \cos^2 \theta - \cos \theta - 1 = 0\) for \(\theta \in [-\text{180}\text{°};\text{180}\text{°}]\).

Factorise the equation

\begin{align*} 2 \cos^2 \theta - \cos \theta - 1 &= 0 \\ (2 \cos \theta + 1)(\cos \theta - 1) &= 0 \\ \therefore 2 \cos \theta + 1 = 0 &\text{ or } \cos \theta - 1 = 0 \end{align*}

Simplify the equations and solve for \(\theta\)

\begin{align*} 2 \cos \theta + 1 &= 0 \\ 2 \cos \theta &= -1 \\ \cos \theta &= -\frac{1}{2} \\ \therefore \text{ref } \angle &= \text{60}\text{°} \\ \text{II quadrant: } \theta &= \text{180}\text{°} - \text{60}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{120}\text{°} + k \cdot \text{360}\text{°} \\ \text{III quadrant: } \theta &= \text{180}\text{°} + \text{60}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{240}\text{°} + k \cdot \text{360}\text{°} \end{align*}

\begin{align*} \cos \theta - 1 &= 0 \\ \cos \theta &= 1 \\ \therefore \text{ref } \angle &= \text{0}\text{°} \\ \text{II and IV quadrants: } \theta &= k \cdot \text{360}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Substitute suitable values of \(k\)

Determine the values of \(\theta\) that lie within the the given interval \(\theta \in [-\text{180}\text{°};\text{180}\text{°}]\) by substituting suitable values of \(k\).

If \(k = -1\),

\begin{align*} \theta &= \text{240}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{240}\text{°} - (\text{360}\text{°}) \\ &= -\text{120}\text{°} \end{align*}

If \(k = 0\),

\begin{align*} \theta &= \text{120}\text{°} + k \cdot \text{360}\text{°} \\ &= \text{120}\text{°} + 0(\text{360}\text{°}) \\ &= \text{120}\text{°} \end{align*}

If \(k = 1\),

\begin{align*} \theta &= k \cdot \text{360}\text{°} \\ &= 0(\text{360}\text{°}) \\ &= \text{0}\text{°} \end{align*}

Alternative method: substitution

We can simplify the given equation by letting \(y = \cos \theta\) and then factorising as:

\begin{align*} 2y^2 - y - 1 &= 0 \\ (2 y + 1)(y - 1) &= 0 \\ \therefore y = -\frac{1}{2} &\text{ or } y = 1 \end{align*}

We substitute \(y = \cos \theta\) back into these two equations and solve for \(\theta\).

Write the final answer

\(\theta = -\text{120}\text{°}\); \(\text{0}\)\(\text{°}\); \(\text{120}\)\(\text{°}\)

Worked example 21: Quadratic trigonometric equations

Find \(\alpha\) if \(2 \sin^2 \alpha - \sin \alpha \cos \alpha = 0\) for \(\alpha \in [\text{0}\text{°};\text{360}\text{°}]\).

Factorise the equation by taking out a common factor

\begin{align*} 2 \sin^2 \alpha - \sin \alpha \cos \alpha &= 0 \\ \sin \alpha (2 \sin \alpha - \cos \alpha) &= 0 \\ \therefore \sin \alpha = 0 &\text{ or } 2 \sin \alpha - \cos \alpha = 0 \end{align*}

Simplify the equations and solve for \(\alpha\)

\begin{align*} \sin \alpha &= 0 \\ \therefore \text{ref } \angle &= \text{0}\text{°} \\ \therefore \alpha &= \text{0}\text{°} + k \cdot \text{360}\text{°} \\ \text{or } \alpha &= \text{180}\text{°} + k \cdot \text{360}\text{°} \\ \text{and since } \text{360}\text{°} &= 2 \times \text{180}\text{°} \\ \text{we therefore have } \alpha &= k \cdot \text{180}\text{°} \end{align*}

\begin{align*} 2 \sin \alpha - \cos \alpha &= 0 \\ 2 \sin \alpha &= \cos \alpha \end{align*}

To simplify further, we divide both sides of the equation by \(\cos \alpha\).

\begin{align*} \frac{2 \sin \alpha}{\cos \alpha} &= \frac{\cos \alpha}{\cos \alpha} \qquad (\cos \alpha \ne 0)\\ 2 \tan \alpha &= 1 \\ \tan \alpha &= \frac{1}{2} \\ \therefore \text{ref } \angle &= \text{26,6}\text{°} \\ \therefore \alpha &= \text{26,6}\text{°} + k \cdot \text{180}\text{°} \end{align*}

where \(k \in \mathbb{Z}\).

Substitute suitable values of \(k\)

Determine the values of \(\alpha\) that lie within the the given interval \(\alpha \in [\text{0}\text{°}; \text{360}\text{°}]\) by substituting suitable values of \(k\).

If \(k = 0\):

\begin{align*} \alpha &= \text{0}\text{°} \\ \text{or } \alpha &= \text{26,6}\text{°} \end{align*}

If \(k = 1\):

\begin{align*} \alpha &= \text{180}\text{°} \\ \text{or } \alpha &= \text{26,6}\text{°} + \text{180}\text{°} \\ &= \text{206,6}\text{°} \end{align*}

If \(k = 2\):

\[\alpha = \text{360}\text{°}\]

Write the final answer

\(\alpha = \text{0}\text{°}\); \(\text{26,6}\)\(\text{°}\); \(\text{180}\)\(\text{°}\); \(\text{206,6}\)\(\text{°}\); \(\text{360}\)\(\text{°}\)

Solving trigonometric equations

Textbook Exercise 6.9

\(\cos 2\theta = 0\)

\begin{align*} \cos 2\theta &= 0\\ \text{ref } \angle &= \text{90}\text{°} \\ \text{I/II quad: } \quad 2\theta &= \text{90}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{45}\text{°} + k \cdot \text{180}\text{°} \\ &= \text{140}\text{°} + k \cdot \text{240}\text{°} \\ \text{III/IV quad: } \quad 2\theta &= \text{270}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{135}\text{°}+ k \cdot \text{180}\text{°} \end{align*}

\(\theta = \text{45}\text{°} + k \cdot \text{180}\text{°}\) or \(\theta = \text{135}\text{°} + k \cdot \text{180}\text{°}\)

\(\sin (\alpha + \text{10}\text{°}) = \frac{\sqrt{3}}{2}\)

\begin{align*} \sin (\alpha + \text{10}\text{°}) &= \frac{\sqrt{3}}{2} \\ \text{ref } \angle &= \text{60}\text{°} \\ \text{I quad: } \quad \alpha + \text{10}\text{°} &= \text{60}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \alpha &= \text{50}\text{°} + k \cdot \text{360}\text{°} \\ \text{III quad: } \alpha + \text{10}\text{°} &= \text{120}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \alpha &= \text{110}\text{°} + k \cdot \text{360}\text{°} \end{align*}

\(\alpha = \text{50}\text{°} + k \cdot \text{360}\text{°}\) or \(\alpha = \text{110}\text{°} + k \cdot \text{360}\text{°}\)

\(2 \cos \frac{\theta}{2} - \sqrt{3} = 0\)

\begin{align*} 2 \cos \frac{\theta}{2} - \sqrt{3} &= 0 \\ \cos \frac{\theta}{2} &= \frac{\sqrt{3}}{2} \\ \text{ref } \angle &= \text{30}\text{°} \\ \text{I quad: } \quad \frac{\theta}{2} &= \text{30}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{60}\text{°} + k \cdot \text{720}\text{°} \\ \text{IV quad: } \frac{\theta}{2} &= \text{330}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{660}\text{°} + k \cdot \text{720}\text{°} \end{align*}

\(\theta = \text{60}\text{°} + k \cdot \text{720}\text{°}\) or \(\theta = \text{660}\text{°} + k \cdot \text{720}\text{°}\)

\(\frac{1}{2} \tan (\beta - \text{30}\text{°}) = -1\)

\begin{align*} \frac{1}{2} \tan (\beta - \text{30}\text{°}) &= -1 \\ \tan (\beta - \text{30}\text{°}) &= -2 \\ \text{ref } \angle &= \text{63,4}\text{°} \\ \text{II quad: } \quad \beta - \text{30}\text{°} &= \text{116,6}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \therefore \beta &= \text{146,6}\text{°} + k \cdot \text{180}\text{°} \end{align*}

\(\beta = \text{146,6}\text{°} + k \cdot \text{180}\text{°}\)

\(5 \cos \theta = \tan \text{300}\text{°}\)

\begin{align*} 5 \cos \theta & = \tan \text{300}\text{°} \\ \cos \theta &= -\text{0,3464}\\ \text{ref } \angle &= \text{69,73}\text{°} \\ \text{II quad: } \quad \theta &= \text{110,27}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \text{III quad: } \quad \theta &= \text{249,73}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \end{align*}

\(\theta = \text{110,27}\text{°} + k \cdot \text{360}\text{°}\) or \(\theta = \text{249,73}\text{°} + k \cdot \text{360}\text{°}\)

\(3 \sin \alpha = -\text{1,5}\)

\begin{align*} 3 \sin \alpha &= -\text{1,5}\\ \sin \alpha &= -\text{0,5}\\ \text{ref } \angle &= \text{30}\text{°} \\ \text{III quad: } \quad \alpha &= \text{210}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \text{IV quad: } \quad \alpha &= \text{330}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \end{align*}

\(\alpha = \text{210}\text{°} + k \cdot \text{360}\text{°}\) or \(\alpha = \text{330}\text{°} + k \cdot \text{360}\text{°}\)

\(\sin 2 \beta = \cos (\beta + \text{20}\text{°})\)

\begin{align*} \sin 2 \beta &= \cos (\beta + \text{20}\text{°})\\ 2 \beta + \beta + \text{20}\text{°} &= \text{90}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 3 \beta &= \text{70}\text{°} + k \cdot \text{360}\text{°} \\ \beta &= \text{23,3}\text{°} + k \cdot \text{120}\text{°} \end{align*}

\(\beta = \text{23,3}\text{°} + k \cdot \text{120}\text{°}\)

\(\text{0,5} \tan \theta + \text{2,5}= \text{1,7}\)

\begin{align*} \text{0,5} \tan \theta + \text{2,5}&= \text{1,7}\\ \tan \theta &= -\text{1,6} \\ \text{ref } \angle &= \text{58}\text{°} \\ \text{III quad: } \quad \theta &= \text{122}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \end{align*}

\(\theta = \text{122}\text{°} + k \cdot \text{180}\text{°}\)

\(\sin (3 \alpha - \text{10}\text{°}) = \sin (\alpha + \text{32}\text{°})\)

\begin{align*} \sin (3 \alpha - \text{10}\text{°}) &= \sin (\alpha + \text{32}\text{°}) \\ 3 \alpha - \text{10}\text{°} &= \alpha + \text{32}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 2 \alpha &= \text{42}\text{°} + k \cdot \text{360}\text{°} \\ \alpha &= \text{21}\text{°} + k \cdot \text{180}\text{°} \\ \text{Or } \quad 3 \alpha - \text{10}\text{°} &= \text{180}\text{°} - (\alpha + \text{32}\text{°} ) + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 4 \alpha &= \text{158}\text{°} + k \cdot \text{360}\text{°} \\ \therefore \alpha &= \text{39,5}\text{°} + k \cdot \text{90}\text{°} \end{align*}

\(\alpha = \text{21}\text{°} + k \cdot \text{180}\text{°}\) or \(\alpha = \text{39,5}\text{°} + k \cdot \text{90}\text{°}\)

\(\sin 2 \beta = \cos 2 \beta\)

\begin{align*} \sin 2 \beta &= \cos 2 \beta \\ \tan 2 \beta &= 1 \\ \text{ref } \angle &= \text{45}\text{°} \\ 2 \beta &= \text{45}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \therefore \beta &= \text{22,5}\text{°} + k \cdot \text{90}\text{°} \end{align*}

\(\beta = \text{22,5}\text{°} + k \cdot \text{90}\text{°}\)

Find \(\theta\) if \(\sin^2 \theta + \frac{1}{2} \sin \theta = 0\) for \(\theta \in [\text{0}\text{°};\text{360}\text{°}]\).

\begin{align*} \sin^2 \theta + \frac{1}{2} \sin \theta &= 0 \\ \sin \theta (\sin \theta + \frac{1}{2}) &= 0 \\ \therefore \sin \theta = 0 &\text{ or } \sin \theta = - \frac{1}{2} \\ \therefore \theta &= \text{0}\text{°}, \text{180}\text{°} \text{ or } \text{360}\text{°} \\ \text{Or } \sin \theta &= - \frac{1}{2} \\ \text{ref } \angle &= \text{30}\text{°} \\ \therefore \theta &= \text{210}\text{°} \text{ or } \text{330}\text{°} \end{align*}

\(\theta = \text{0}\text{°}, \text{180}\text{°}, \text{210}\text{°}, \text{330}\text{°} \text{ or } \text{360}\text{°}\)

\(2 \cos^2 \theta - 3 \cos \theta = 2\)

\begin{align*} 2 \cos^2 \theta - 3 \cos \theta &= 2 \\ (2\cos \theta + 1)(\cos \theta - 2) &= 0 \\ \therefore \cos \theta = -\frac{1}{2} &\text{ or } \cos \theta = 2 \\ \text{For } \cos \theta &= 2 \\ \therefore &\text{No solution} \\ \text{For } \cos \theta &= -\frac{1}{2} \\ \text{ref } \angle &= \text{60}\text{°} \\ \text{II quad: } \theta &= \text{180}\text{°} - \text{60}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{120}\text{°} + k \cdot \text{360}\text{°} \\ \text{III quad: } \theta &= \text{180}\text{°} + \text{60}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{240}\text{°}+ k \cdot \text{360}\text{°} \end{align*}

\(\theta = \text{120}\text{°} + k \cdot \text{360}\text{°}\) or \(\theta = \text{240}\text{°} + k \cdot \text{360}\text{°}\)

\(3 \tan^2 \theta + 2 \tan \theta = 0\)

\begin{align*} 3 \tan^2 \theta + 2 \tan \theta &= 0 \\ \tan \theta (3 \tan \theta + 2)&= 0 \\ \therefore \tan \theta = -\frac{2}{3} &\text{ or } \tan \theta = 0 \\ \text{For } \tan \theta &= -\frac{1}{2} \\ \theta &= \text{0}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \text{For } \tan \theta &= -\frac{2}{3} \\ \text{ref } \angle &= \text{33,7}\text{°} \\ \theta &= \text{180}\text{°} - \text{33,7}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \therefore \theta &= \text{146,3}\text{°} + k \cdot \text{180}\text{°} \end{align*}

\(\theta = \text{0}\text{°} + k \cdot \text{180}\text{°}\) or \(\theta = \text{146,3}\text{°} + k \cdot \text{180}\text{°}\)

\(\cos^2 \alpha = \text{0,64}\)

\begin{align*} \cos^2 \alpha &= \text{0,64} \\ \therefore \cos \alpha &= \pm \text{0,8} \\ \text{For } \cos \alpha &= - \text{0,8} \\ \text{ref } \angle &= \text{36,9}\text{°} \\ \text{II quad: } \alpha &= \text{180}\text{°} - \text{36,9}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \alpha &= \text{143,1}\text{°} + k \cdot \text{360}\text{°} \\ \text{For } \cos \alpha &= \text{0,8} \\ \text{III quad: } \alpha &= \text{180}\text{°} + \text{36,9}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \alpha &= \text{216,9}\text{°}+ k \cdot \text{360}\text{°} \\ \text{IV quad: } \alpha &= \text{360}\text{°} - \text{36,9}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ \therefore \alpha &= \text{323,1}\text{°}+ k \cdot \text{360}\text{°} \end{align*}

\(\alpha = \text{36,9}\text{°} + k \cdot \text{360}\text{°}\) or \(\alpha = \text{143,1}\text{°} + k \cdot \text{360}\text{°}\) or \(\alpha = \text{216,9}\text{°} + k \cdot \text{360}\text{°}\) or \(\alpha = \text{323,1}\text{°} + k \cdot \text{360}\text{°}\)

\(\sin (4\beta + \text{35}\text{°}) = \cos (\text{10}\text{°} - \beta)\)

\begin{align*} \sin (4\beta + \text{35}\text{°}) &= \cos (\text{10}\text{°} - \beta) \\ \sin (4\beta + \text{35}\text{°}) &= \sin \left( \text{90}\text{°} (\text{10}\text{°} - \beta) \right) \\ \sin (4\beta + \text{35}\text{°}) &= \sin \left( \text{80}\text{°} + \beta \right) \\ 4\beta + \text{35}\text{°} &= \text{80}\text{°} + \beta + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 3\beta &= \text{45}\text{°} + k \cdot \text{360}\text{°} \\ \beta &= \text{15}\text{°} + k \cdot \text{120}\text{°} \\ \text{Or } \quad (4\beta + \text{35}\text{°}) + (\text{10}\text{°} - \beta) &= \text{270}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 3\beta &= \text{225}\text{°} + k \cdot \text{360}\text{°} \\ \beta &= \text{75}\text{°} + k \cdot \text{120}\text{°} \end{align*}

\(\beta = \text{15}\text{°} + k \cdot \text{120}\text{°}\) or \(\beta = \text{75}\text{°} + k \cdot \text{120}\text{°}\)

\(\sin (\alpha + \text{15}\text{°}) = 2 \cos (\alpha + \text{15}\text{°})\)

\begin{align*} \sin (\alpha + \text{15}\text{°}) &= 2 \cos (\alpha + \text{15}\text{°}) \\ \dfrac{\sin (\alpha + \text{15}\text{°})}{\cos (\alpha + \text{15}\text{°})} &= 2 \\ \tan (\alpha + \text{15}\text{°}) &= 2 \\ \text{ref } \angle &= \text{63,4}\text{°} \\ \alpha + \text{15}\text{°} &= \text{63,4}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \alpha &= \text{48,4}\text{°} + k \cdot \text{180}\text{°} \end{align*}

\(\alpha = \text{48,4}\text{°} + k \cdot \text{180}\text{°}\)

\(\sin^2 \theta - 4\cos^2 \theta = 0\)

\begin{align*} \sin^2 \theta - 4\cos^2 \theta &= 0 \\ (\sin \theta - 2\cos^2 \theta)(\sin \theta + 2\cos^2 \theta) &= 0 \\ \therefore \sin \theta - 2\cos^2 \theta &=0 \\ \sin \theta &= 2\cos^2 \theta \\ \frac{\sin \theta}{\cos \theta} &= 2 \\ \tan \theta &= 2 \\ \text{ref } \angle &= \text{63,4}\text{°} \\ \theta &= \text{63,4}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \text{Or } \sin \theta + 2\cos^2 \theta &=0 \\ \sin \theta &= -2\cos^2 \theta \\ \frac{\sin \theta}{\cos \theta} &= -2 \\ \tan \theta &= -2 \\ \text{ref } \angle &= -\text{63,4}\text{°} + \text{180}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \theta &= \text{116,6}\text{°} + k \cdot \text{180}\text{°} \end{align*}

\(\theta = \text{63,4}\text{°} + k \cdot \text{180}\text{°}\) or \(\theta = \text{116,6}\text{°} + k \cdot \text{180}\text{°}\)

\(\dfrac{\cos (2 \theta + \text{30}\text{°})}{2} + \text{0,38} = 0\)

\begin{align*} \dfrac{\cos (2 \theta + \text{30}\text{°})}{2} + \text{0,38} &= 0 \\ \dfrac{\cos (2 \theta + \text{30}\text{°})}{2} &= -\text{0,38} \\ \cos (2 \theta + \text{30}\text{°}) &= -\text{0,76} \\ \text{ref } \angle &= \text{40,5}\text{°} \\ 2 \theta + \text{30}\text{°}) &= \text{180}\text{°} - \text{40,5}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 2 \theta &= \text{109,5}\text{°} + k \cdot \text{360}\text{°} \\ \theta &= \text{54,8}\text{°} + k \cdot \text{180}\text{°} \\ \text{Or } \quad 2 \theta + \text{30}\text{°}) &= \text{180}\text{°} + \text{40,5}\text{°} + k \cdot \text{360}\text{°} , k \in \mathbb{Z} \\ 2 \theta &= \text{190,5}\text{°} + k \cdot \text{360}\text{°} \\ \theta &= \text{95,25}\text{°} + k \cdot \text{180}\text{°} \end{align*}

\(\theta = \text{54,8}\text{°} + k \cdot \text{180}\text{°}\) or \(\theta = \text{95,25}\text{°} + k \cdot \text{180}\text{°}\)

Find \(\beta\) if \(\frac{1}{3} \tan \beta = \cos \text{200}\text{°}\) for \(\beta \in [-\text{180}\text{°};\text{180}\text{°}]\).

\begin{align*} \frac{1}{3} \tan \beta &= \cos \text{200}\text{°} \\ \frac{1}{3} \tan \beta &= -\text{0,9396} \\ \tan \beta &= -\text{2,819} \\ \text{ref } \angle &= \text{70,5}\text{°} \\ \beta &= \text{180}\text{°} - \text{70,47}\text{°} + k \cdot \text{180}\text{°} , k \in \mathbb{Z} \\ \beta &= \text{109,5}\text{°} + k \cdot \text{180}\text{°} \\ \therefore \beta = -\text{70,5}\text{°} &\text{ or } \beta = \text{109,5}\text{°} \end{align*}

\(\beta = -\text{70,5}\text{°}\) or \(\beta = \text{109,5}\text{°}\)

6.3 Reduction formula

Table of Contents

6.5 Area, sine, and cosine rules