\(\sin p + 3 \sin p = 4 \sin p\)
6.1 Revision
|
Previous
End of chapter exercises
|
Next
6.2 Trigonometric identities
|
Chapter 6: Trigonometry
- Emphasize that the area/sine/cosine rule does not require a right-angled triangle.
- Encourage learners to use the appropriate form of the area/sine/cosine rule.
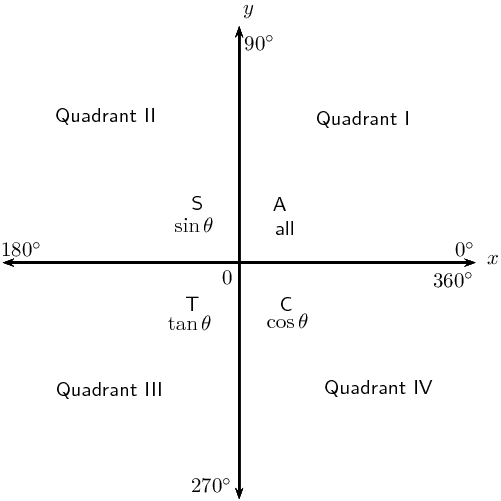
- Remind learners that angles in the Cartesian plane are always measured from the positive x-axis.
- Important to note that:
- \((270 \pm x)\) is not included in the section on reduction formulae.
- co-function for tangent is not included.
- Remind learners to check that their answers are within the required interval.
- For the general solution, determine the solution in the correct quadrants and within the required interval.
- Do not label all triangles as \(ABC\). Learners must be able to apply the formulae with different notations and in different contexts.
- Do not treat identities as equations: do NOT use = sign between the two expressions in an identity. Keep the LHS and RHS separate.
- To prove identities, we usually manipulate the more complicated expression till it looks the same as the more simple expression.
6.1 Revision (EMBHG)
Trigonometric ratios
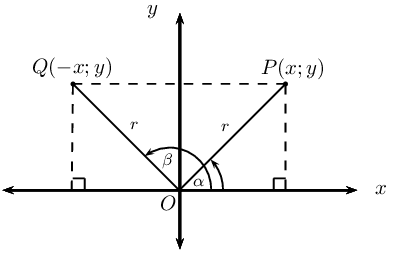
We plot the points \(P(x;y)\) and \(Q(-x;y)\) in the Cartesian plane and measure the angles from the positive \(x\)-axis to the terminal arms \((OP \text{ and } OQ)\).
\(P(x;y)\) lies in the first quadrant with \(P\hat{O}X = \alpha\) and \(Q(-x;y)\) lies in the second quadrant with \(Q\hat{O}X = \beta\).
Using the theorem of Pythagoras we have that
\begin{align*} OP^2 &= x^2 + y^2 \\ \text{And }OQ^2 &= (-x)^2 + y^2 \\ &= x^2 + y^2 \\ \therefore OP &= OQ \end{align*}Let \(OP = OQ = r\).
Trigonometric ratios
\begin{align*} \sin \alpha &= \frac{y}{r} \\ \cos \alpha &= \frac{x}{r}\\ \tan \alpha &= \frac{y}{x} \end{align*}In the second quadrant we notice that \(-x < 0\)
\begin{align*} \sin \beta &= \frac{y}{r} \\ \cos \beta &= -\frac{x}{r}\\ \tan \beta &= -\frac{y}{x} \end{align*}Similarily, in the third and fourth quadrants the sign of the trigonometric ratios depends on the signs of \(x\) and \(y\):
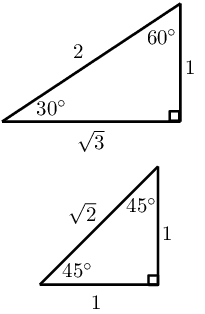
Special angles
|
θ |
\(\text{0}\)\(\text{°}\) |
\(\text{30}\)\(\text{°}\) |
\(\text{45}\)\(\text{°}\) |
\(\text{60}\)\(\text{°}\) |
\(\text{90}\)\(\text{°}\) |
| \(\cos θ\) |
\(\text{1}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{2}}\) |
\(\frac{1}{2}\) |
\(\text{0}\) |
| \(\sin θ\) |
\(\text{0}\) |
\(\frac{1}{2}\) |
\(\frac{1}{\sqrt{2}}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\text{1}\) |
| \(\tan θ\) |
\(\text{0}\) |
\(\frac{1}{\sqrt{3}}\) |
\(\text{1}\) |
\(\sqrt{3}\) |
undef |
Solving equations
Worked example 1: Solving equations
Determine the values of \(a\) and \(b\) in the right-angled triangle \(TUW\) (correct to one decimal place):
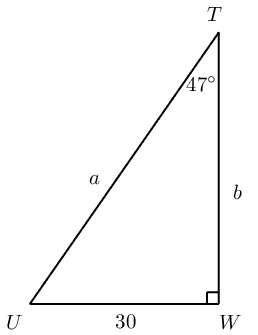
Identify the opposite and adjacent sides and the hypotenuse
Determine the value of \(a\)
\begin{align*} \sin \theta &= \frac{\text{opposite side}}{\text{hypotenuse}} \\ \sin \text{47}\text{°} &= \frac{30}{a} \\ a &= \frac{30}{\sin \text{47}\text{°}} \\ \therefore a &= \text{41,0} \end{align*}Determine the value of \(b\)
Always try to use the information that is given for calculations and not answers that you have worked out in case you have made an error. For example, avoid using \(a = \text{41,0}\) to determine the value of \(b\).
\begin{align*} \tan \theta &= \frac{\text{opposite side}}{\text{adjacent side}} \\ \tan \text{47}\text{°} &= \frac{30}{b} \\ b &= \frac{30}{\tan \text{47}\text{°}} \\ \therefore b &= \text{28,0} \end{align*}Write the final answer
\(a = \text{41,0}\) units and \(b = \text{28,0}\) units.
Finding an angle
Worked example 2: Finding an angle
Calculate the value of \(\theta\) in the right-angled triangle \(MNP\) (correct to one decimal place):
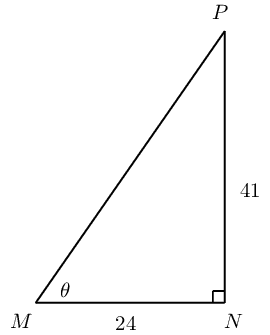
Identify the opposite and adjacent sides and the hypotenuse
Determine the value of \(\theta\)
\begin{align*} \tan \theta &= \frac{\text{opposite side}}{\text{adjacent side}} \\ \tan \theta &= \frac{41}{24} \\ \therefore \theta &= \tan^{-1} \left( \frac{41}{24} \right) \\ \theta &= \text{59,7}\text{°} \end{align*}Worked example 3: Finding an angle
Given \(2 \sin \frac{\theta}{2} = \cos \text{43}\text{°}, \text{ for } \theta \in [\text{0}\text{°};\text{90}\text{°}]\), determine the value of \(\theta\) (correct to one decimal place).
Simplify the equation
Avoiding rounding off in calculations until you have determined the final answer. In the calculation below, the dots indicate that the number has not been rounded so that the answer is as accurate as possible.
\begin{align*} 2 \sin \frac{\theta}{2} &= \cos \text{43}\text{°} \\ \sin \frac{\theta}{2} &= \frac{\cos \text{43}\text{°}}{2} \\ \frac{\theta}{2} &= \sin^{-1} (\text{0,365} \ldots ) \\ \theta &= 2 (\text{21,449} \ldots ) \\ \therefore \theta &= \text{42,9}\text{°} \end{align*}Two-dimensional problems
Worked example 4: Flying a kite
Thelma flies a kite on a \(\text{22}\) \(\text{m}\) piece of string and the height of the kite above the ground is \(\text{20,4}\) \(\text{m}\). Determine the angle of inclination of the string (correct to one decimal place).
Draw a sketch and identify the opposite and adjacent sides and the hypotenuse
Let the angle of inclination of the string be \(\theta\).
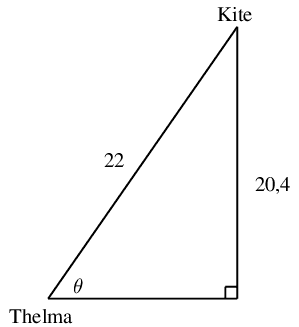
Use an appropriate trigonometric ratio to find \(\theta\)
\begin{align*} \sin \theta &= \frac{\text{opposite side}}{\text{hypotenuse}} \\ &= \frac{\text{20,4}}{22} \\ \theta &= \sin^{-1} (\text{0,927} \ldots ) \\ \therefore \theta &= \text{68,0}\text{°} \end{align*}Revision
If \(p = \text{49}\text{°}\) and \(q = \text{32}\text{°}\), use a calculator to determine whether the following statements are true of false:
\(\dfrac{\sin q}{\cos q} = \tan q\)
\(\cos (p - q) = \cos p - \cos q\)
\(\sin (2p) = 2\sin p \cos p\)
Determine the following angles (correct to one decimal place):
\(\cos \alpha = \text{0,64}\)
\(\sin \theta + 2 = \text{2,65}\)
\(\frac{1}{2} \cos 2\beta = \text{0,3}\)
\(\tan \frac{\theta}{3} = \sin \text{48}\text{°}\)
\(\cos 3p = \text{1,03}\)
\(2 \sin 3\beta + 1 = \text{2,6}\)
\(\dfrac{\sin \theta}{\cos \theta} = 4\frac{2}{3}\)
In \(\triangle ABC, A\hat{C}B = \text{30}\text{°}, AC = \text{20}\text{ cm} \text{ and } BC = \text{22}\text{ cm}\). The perpendicular line from \(A\) intersects \(BC\) at \(T\).
Determine:
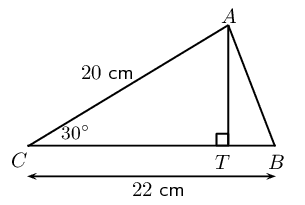
the length \(TC\)
the length \(AT\)
the angle \(B\hat{A}T\)
A rhombus has a perimeter of \(\text{40}\text{ cm}\) and one of the internal angles is \(\text{30}\text{°}\).
Determine the length of the sides.
Determine the lengths of the diagonals.
Diagonals of a rhombus bisect each other at right-angles and also bisect interior angles. Let the shorter diagonal be \(2x\):
\begin{align*} \sin \text{15}\text{°} &= \frac{x}{10} \\ \therefore x &= 10 \sin \text{15}\text{°} \\ \therefore \text{Shorter diagonal }&= 2 \times 10 \sin \text{15}\text{°} \\ &= \text{5,2}\text{ cm} \end{align*}Let the longer diagonal be \(2y\):
\begin{align*} \cos \text{15}\text{°} &= \frac{y}{10} \\ \therefore y &= 10 \cos \text{15}\text{°} \\ \therefore \text{Longer diagonal }&= 2 \times 10 \cos \text{15}\text{°} \\ &= \text{19,3}\text{ cm} \end{align*}Calculate the area of the rhombus.
Simplify the following without using a calculator:
\(2 \sin \text{45}\text{°} \times 2 \cos \text{45}\text{°}\)
\(\cos^2 \text{30}\text{°} - \sin^2 \text{60}\text{°}\)
\(\sin \text{60}\text{°} \cos \text{30}\text{°} - \cos \text{60}\text{°} \sin \text{30}\text{°} - \tan \text{45}\text{°}\)
\(4 \sin \text{60}\text{°} \cos \text{30}\text{°} - 2 \tan \text{45}\text{°} + \tan \text{60}\text{°} - 2 \sin \text{60}\text{°}\)
\(\sin \text{60}\text{°} \times \sqrt{2 \tan \text{45}\text{°} + 1 } - \sin \text{30}\text{°}\)
Given the diagram below.
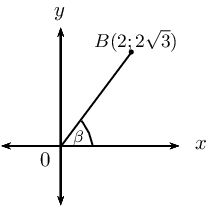
Determine the following without using a calculator:
\(\beta\)
\(\cos \beta\)
\(\cos^2 \beta + \sin^2 \beta\)
The \(\text{10}\) \(\text{m}\) ladder of a fire truck leans against the wall of a burning building at an angle of \(\text{60}\text{°}\). The height of an open window is \(\text{9}\) \(\text{m}\) from the ground. Will the ladder reach the window?
|
Previous
End of chapter exercises
|
Table of Contents |
Next
6.2 Trigonometric identities
|
