Find the first five terms of the quadratic sequence defined by:
\({T}_{n}={n}^{2}+2n+1\)
\(-4; 9; 16; 25; 36\)
End of chapter exercises
|
Previous
3.3 Summary
|
Next
4.1 Revision
|
End of chapter exercises
Textbook Exercise 3.4
Determine whether each of the following sequences is:
- a linear sequence,
- a quadratic sequence,
- or neither.
\(6;9;14;21;30;...\)
\begin{align*}
\text{First differences: } &= 3; 5; 7; 9; \\
\text{Second difference: } &= 2
\end{align*}
Quadratic sequence
\(1;7;17;31;49;...\)
\begin{align*}
\text{First differences: } &= 6; 10; 14; 18 \\
\text{Second difference: } &= 4
\end{align*}
Quadratic sequence
\(8;17;32;53;80;...\)
\begin{align*}
\text{First differences: } &= 9; 15; 21; 27 \\
\text{Second difference: } &= 6
\end{align*}
Quadratic sequence
\(9;26;51;84;125;...\)
\begin{align*}
\text{First differences: } &= 17; 25; 33; 41 \\
\text{Second difference: } &= 8
\end{align*}
Quadratic sequence
\(2;20;50;92;146;...\)
\begin{align*}
\text{First differences: } &= 18; 30; 42; 54 \\
\text{Second difference: } &= 12
\end{align*}
Quadratic sequence
\(5;19;41;71;109;...\)
\begin{align*}
\text{First differences: } &= 14; 22; 30; 38 \\
\text{Second difference: } &= 8
\end{align*}
Quadratic sequence
\(2;6;10;14;18;...\)
\[\text{First difference: } = 4\]
Linear sequence
\(3;9;15;21;27;...\)
\[\text{First difference: } = 6\]
Linear sequence
\(1;\text{2,5};5;\text{8,5};13;...\)
\begin{align*}
\text{First differences: } &= \text{1,5};~ \text{2,5};~ \text{3,5};~ \text{4,5} \\
\text{Second difference: } &= 1
\end{align*}
Quadratic sequence
\(10;24;44;70;102;...\)
\begin{align*}
\text{First differences: } &= 14; 20; 26; 32 \\
\text{Second difference: } &= 16
\end{align*}
Quadratic sequence
\(2\frac{1}{2}; 6; 10\frac{1}{2}; 16; 22\frac{1}{2}; \ldots\)
\begin{align*}
\text{First differences: } &= \text{3,5};~ \text{4,5};~ \text{5,5};~ \text{6,5} \\
\text{Second difference: } &= 1
\end{align*}
Quadratic sequence
\(3p^2; 6p^2; 9p^2; 12p^2; 15p^2; \ldots\)
\[\text{First difference: } = 3p^2\]
Linear sequence
\(2k; 8k; 18k; 32k; 50k; \ldots\)
\begin{align*}
\text{First differences: } &= 6k; 10k; 14k; 18k \\
\text{Second difference: } &= 4k
\end{align*}
Quadratic sequence
Given the pattern: \(16; x; 46; \ldots\), determine the value of \(x\) if the pattern is linear.
\begin{align*}
x - 16 &= 46 - x \\
2x &= 62 \\
\therefore x &= 31
\end{align*}
Given \(T_n = 2n^2\), for which value of \(n\) does \(T_n = 242\)?
\begin{align*}
2n^2 &= 242 \\
n^2 &= 121 \\
\therefore n &= 11
\end{align*}
Given \({T}_{n}=3{n}^{2}\), find \({T}_{11}\).
\begin{align*}
T_n &= 3n^2 \\
\therefore T_11 &= 3(11)^2 \\
&= 363
\end{align*}
Given \(T_n = n^2+4\), for which value of \(n\) does \(T_n = 85\)?
\begin{align*}
n^2 + 4 &= 85 \\
n^2 &= 81 \\
\therefore n &= 9
\end{align*}
Given \({T}_{n}=4{n}^{2}+3n-1\), find \({T}_{5}\).
\begin{align*}
T_n &= 4n^2 + 3n - 1 \\
\therefore T_5 &= 4(5)^2 + 3(5) - 1\\
&= 100 + 15 - 1 \\
&= 114
\end{align*}
Given \(T_n = \dfrac{3}{2}n^2\), for which value of \(n\) does \(T_n = 96\)?
\begin{align*}
\dfrac{3}{2}n^2 &= 96 \\
n^2 &= 96 \times \frac{2}{3} \\
&= 64 \\
\therefore n &= 8
\end{align*}
For each of the following patterns, determine:
- the next term in the pattern,
- and the general term,
- the tenth term in the pattern.
\(3; 7; 11; 15; \ldots\)
\begin{align*}
d &= 7 - 3 \\
&= 4 \\
T_5 &= 15 + 4 \\
&= 19 \\
T_n &= 4n - 1 \\
T_{10} &= 4(10) - 1 \\
&= 39
\end{align*}
\(17; 12; 7; 2; \ldots\)
\begin{align*}
d &= 12 - 17 \\
&= -5 \\
T_5 &= 2 - 5 \\
&= -3 \\
T_n &= 22 - 5n \\
T_{10} &= 22 - 5(10) \\
&= -28
\end{align*}
\(\frac{1}{2}; 1; 1\frac{1}{2}; 2; \ldots\)
\begin{align*}
d &= 1 - \frac{1}{2} \\
&= \frac{1}{2} \\
T_5 &= 2 + \frac{1}{2} \\
&= 2 \frac{1}{2} \\
T_n &= \frac{1}{2}n \\
T_{10} &= \frac{1}{2}(10) \\
&= 5
\end{align*}
\(a; a+b; a+2b; a+3b; \ldots\)
\begin{align*}
d &= a + b - a \\
&= b \\
T_5 &= a + 3b + b \\
&= a + 4b \\
T_n &= a - b + bn \\
T_{10} &= a - b + b(10) \\
&= a + 9b
\end{align*}
\(1; -1; -3; -5; \ldots\)
\begin{align*}
d &= -1 - 1 \\
&= -2 \\
T_5 &= -5 -2 \\
&= -7 \\
T_n &= 3 - 2n \\
T_{10} &= 3 - 2(10) \\
&= -17
\end{align*}
For each of the following sequences, find the equation for the general term and then use the equation to find \({T}_{100}\).
\(4;7;12;19;28;...\)
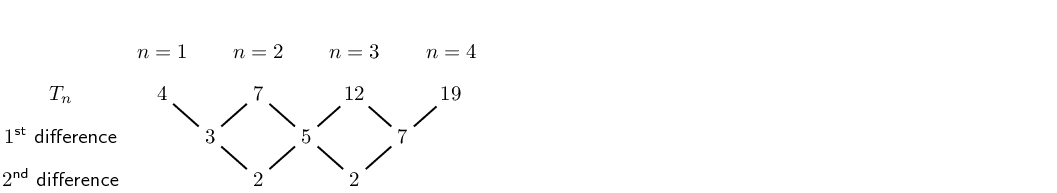
\(2;8;14;20;26;...\)
\begin{align*}
d &= 8 - 2 \\
&= 6 \\
\therefore T_n &= 6n - 4
\end{align*}
\begin{align*}
T_n &= 6n - 4 \\
\therefore T_{100} &= 6(100) - 4 \\
&= 596
\end{align*}
\(7;13;23;37;55;...\)
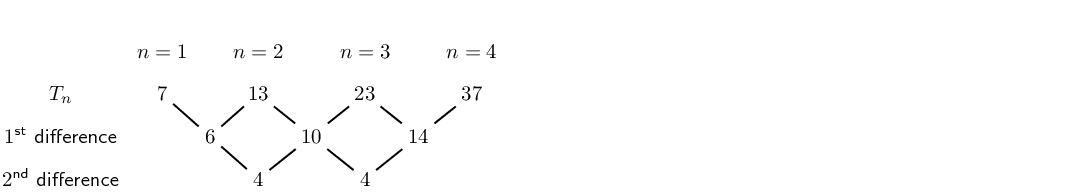
\(5;14;29;50;77;...\)
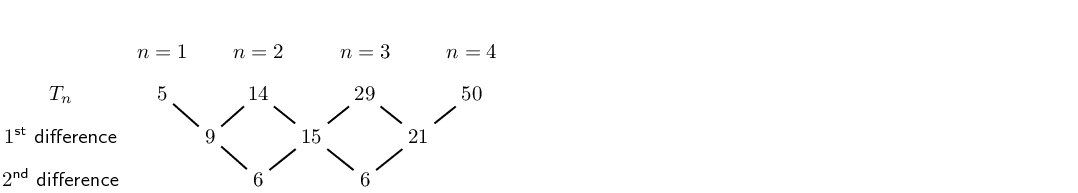
Given: \(T_n = 3n-1\)
Write down the first five terms of the sequence.
\(2; 5; 8; 11; 14\)
What do you notice about the difference between any two consecutive terms?
Constant difference, \(d=3\)
Will this always be the case for a linear sequence?
Yes
Given the following sequence: \(-15; -11; -7; \ldots ; 173\)
Determine the equation for the general term.
\begin{align*}
d &= -11 - (-15) \\
&= 4 \\
T_n &= 4n - 19
\end{align*}
Calculate how many terms there are in the sequence.
\begin{align*}
T_n &= 4n - 19 \\
173 &= 4n - 19 \\
192 &= 4n \\
\therefore 48 &= n
\end{align*}
Given \(3; 7; 13; 21; 31; \ldots\)
Thabang determines that the general term is \(T_n = 4n - 1\). Is he correct? Explain.
\begin{align*}
\text{First differences: } &= 4; 6; 8; 10 \\
\text{Second difference: } &= 2
\end{align*}
Thabang's general term \(T_n = 4n - 1\) describes a linear sequence and this is a quadratic sequence.
Cristina determines that the general term is \(T_n = n^2 + n + 1\). Is she correct? Explain.
\begin{align*}
T_n &= an^2 + bn + c \\
\text{Second difference: } 2a &= 2 \\
\therefore a &= 1 \\
3a + b &= 4 \\
b &= 4 - 3(1) \\
\therefore b &= 1 \\
a + b + c &= 3 \\
\therefore c &= 3 - a - b \\
&= 3 - 1 - 1 \\
\therefore c &= 1 \\
\therefore T_n &= n^2 + n + 1
\end{align*}
Given the following pattern of blocks:
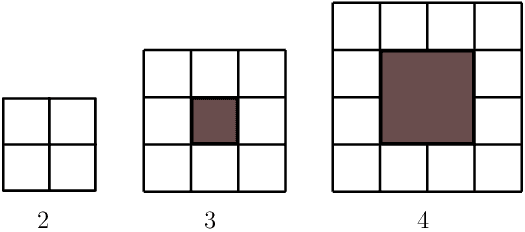
Draw pattern \(\text{5}\).
Complete the table below:
| pattern number \((n)\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{10}\) | \(\text{250}\) | \(n\) |
| number of white blocks \((w)\) | \(\text{4}\) | \(\text{8}\) |
| pattern number \((n)\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{10}\) | \(\text{250}\) | \(n\) |
| number of white blocks \((w)\) | \(\text{4}\) | \(\text{8}\) | \(\text{12}\) | \(\text{16}\) | \(\text{36}\) | \(\text{996}\) | \(4n - 4\) |
Is this a linear or a quadratic sequence?
Linear
Cubes of volume \(\text{1}\) \(\text{cm$^{3}$}\) are stacked on top of each other to form a tower:
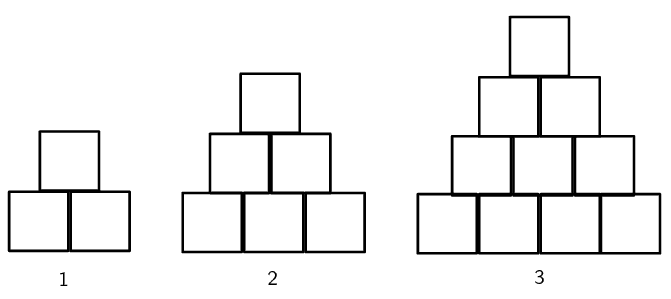
Complete the table for the height of the tower:
| tower number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{10}\) | \(n\) |
| height of tower \((h)\) | \(\text{2}\) |
| tower number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{10}\) | \(n\) |
| height of tower \((h)\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{11}\) | \(n+1\) |
What type of sequence is this?
Linear
Now consider the number of cubes in each tower and complete the table below:
| tower number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) |
| number of cubes \((c)\) | \(\text{3}\) |
| tower number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) |
| number of cubes \((c)\) | \(\text{3}\) | \(\text{6}\) | \(\text{10}\) | \(\text{15}\) |
What type of sequence is this?
Quadratic
Determine the general term for this sequence.
\begin{align*}
T_n &= an^2 + bn + c \\
\text{Second difference: } 2a &= 1 \\
\therefore a &= \frac{1}{2} \\
3a + b &= 3 \\
b &= 3 - 3(\frac{1}{2}) \\
\therefore b &= \frac{3}{2} \\
a + b + c &= 3 \\
\therefore c &= 3 - a - b \\
&= 3 - \frac{1}{2} - \frac{3}{2} \\
\therefore c &= 1 \\
\therefore T_n &= \frac{1}{2}n^2 + \frac{3}{2}n + 1
\end{align*}
How many cubes are needed for tower number \(\text{21}\)?
\begin{align*}
T_n &= \frac{1}{2}n^2 + \frac{3}{2}n + 1 \\ \therefore T_{21} &= \frac{1}{2}(21)^{2}+
\frac{3}{2}(21) + 1 \\
&= \frac{441}{2} + \frac{63}{2} + \frac{2}{2} \\
&= 253
\end{align*}
How high will a tower of \(\text{496}\) cubes be?
\begin{align*}
T_n &= \frac{1}{2}n^2 + \frac{3}{2}n + 1\\ 496 &= \frac{1}{2}n^2 + \frac{3}{2}n + 1 \\
0 &= \frac{1}{2}n^2 + \frac{3}{2}n - 495 \\
&= n^2 + 3n - 990 \\
&= (n - 30)(n + 33) \\
\therefore n = 30 &\text{ or } n = -33 \\
\therefore n &= 30 \\
\text{And } h &= n + 1 \\
&= 30 + 1 \\
&= \text{31}\text{ cm}
\end{align*}
A quadratic sequence has a second term equal to \(\text{1}\), a third term equal to \(-\text{6}\) and a fourth term equal to \(-\text{14}\).
Determine the second difference for this sequence.
\begin{align*}
T_3 - T_2 &= -6 -(1) \\
&= -7 \\
T_4 - T_3 &= -14 - (-6) \\
&= -8 \\
\therefore \text{Second difference} &= -1
\end{align*}
Hence, or otherwise, calculate the first term of the pattern.
\begin{align*}
T_{1} &= 1 + 6 \\
&= 7
\end{align*}
There are \(\text{15}\) schools competing in the U16 girls hockey championship and every team must play two matches — one home match and one away match.
Use the given information to complete the table:
| no. of schools | no. of matches |
| \(\text{1}\) | \(\text{0}\) |
| \(\text{2}\) | |
| \(\text{3}\) | |
| \(\text{4}\) | |
| \(\text{5}\) |
| no. of schools | no. of matches |
| \(\text{1}\) | \(\text{0}\) |
| \(\text{2}\) | \(\text{2}\) |
| \(\text{3}\) | \(\text{6}\) |
| \(\text{4}\) | \(\text{12}\) |
| \(\text{5}\) | \(\text{20}\) |
Calculate the second difference.
\begin{align*}
T_2 - T_1 &= 2 - 0 \\
&= 2 \\
T_3 - T_2 &= 6 - 2 \\
&= 4 \\
T_4 - T_3 &= 12 -6 \\
&= 6 \\
T_5 - T_4 &= 20 - 12 \\
&= 8 \\
\therefore \text{Second difference} &= 2
\end{align*}
Determine a general term for the sequence.
\begin{align*}
T_n &= an^2 + bn + c \\
\text{Second difference: } 2a &= 2 \\
\therefore a &= 1 \\
3a + b &= 2 \\
b &= 2 - 3(1) \\
\therefore b &= -1 \\
a + b + c &= 0 \\
\therefore c &= - a - b \\
&= -1 - (-1) \\
\therefore c &= 0 \\
\therefore T_n &= n^2 -n
\end{align*}
How many matches will be played if there are \(\text{15}\) schools competing in the championship?
\begin{align*}
T_n &= n^2 -n \\
T_{15} &= (15)^2 - 15 \\
&= 225 - 15 \\
&= 210
\end{align*}
If \(\text{600}\) matches must be played, how many schools are competing in the championship?
\begin{align*}
T_n &= n^2 -n \\
600 &= n^2 -n \\
0 &= n^2 -n - 600\\
&= (n - 25)(n + 24)\\
\therefore n = 25 &\text{ or } n = -24 \\
\therefore n &= 25
\end{align*}
The first term of a quadratic sequence is \(\text{4}\), the third term is \(\text{34}\) and the common second difference is \(\text{10}\). Determine the first six terms in the sequence.
\begin{align*}
\text{Let } T_2 &= x \\
\therefore T_2 - T_1 &= x - 4 \\
\text{And } T_3 - T_2 &= 34 - x \\
\text{Second difference } &= (T_3 - T_2) - (T_2 - T_1) \\
&= (34 - x) - (x - 4)\\
\therefore 10 &= 38 - 2x \\
2x &= 28 \\
\therefore x &= 14
\end{align*}
\(4; 14; 34; 64; 104; 154\)
Challenge question:
Given that the general term for a quadratic sequences is \(T_n = an^2 + bn + c\), let \(d\) be the first difference and \(D\) be the second common difference.
Show that \(a = \dfrac{D}{2}\).
\begin{align*}
T_n &= an^2 + bn +c \\
T_1 &= a(1)^2 + b(1) +c \\
&= a + b + c \\
T_2 &= a(2)^2 + b(2) +c \\
&= 4a + 2b + c\\
T_3 &= a(3)^2 + b(3) +c \\
&= 9a + 6b + c\\
\text{First difference } d &= T_2 - T_1 \\
\therefore d &= (4a + 2b + c) - (a + b + c ) \\
&= 3a + b \\
\therefore b &= d - 3a \\
\text{Second difference } D &= (T_3 - T_2) - (T_2 - T_1)\\
\therefore D &= (5a + b) - (3a + b) \\
&= 2a \\
\therefore a &= \dfrac{D}{2}
\end{align*}
Show that \(b = d - \dfrac{3}{2}D\).
\begin{align*}
a &= \dfrac{D}{2} \\
b &= d - 3a \\
\therefore b &= d - 3 \left( \dfrac{D}{2} \right) \\
&= d - \dfrac{3}{2} D
\end{align*}
Show that \(c = T_1 - d + D\).
\begin{align*}
T_1 &= a + b + c \\
\therefore c &= T_1 - a - b \\
&= T_1 - \left( \dfrac{D}{2} \right) - \left( d - \dfrac{3}{2}D \right) \\
&= T_1 - \dfrac{D}{2} - d + \dfrac{3}{2}D \\
&= T_1 - d + D
\end{align*}
Hence, show that \(T_n = \dfrac{D}{2}n^2 + \left(d - \dfrac{3}{2}D\right)n + \left(T_1 -d + D\right)\).
\begin{align*}
T_n &= an^2 + bn +c \\
\therefore T_n &= \dfrac{D}{2}n^2 + \left( d - \dfrac{3}{2}D \right)n + \left( T_1 - d + D
\right)
\end{align*}
|
Previous
3.3 Summary
|
Table of Contents |
Next
4.1 Revision
|