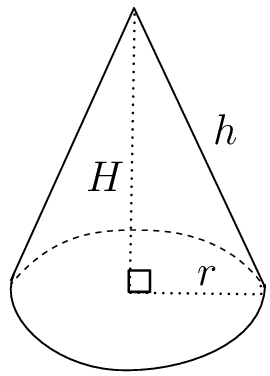
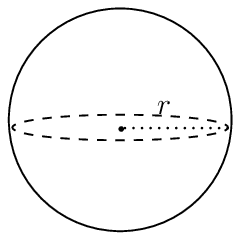
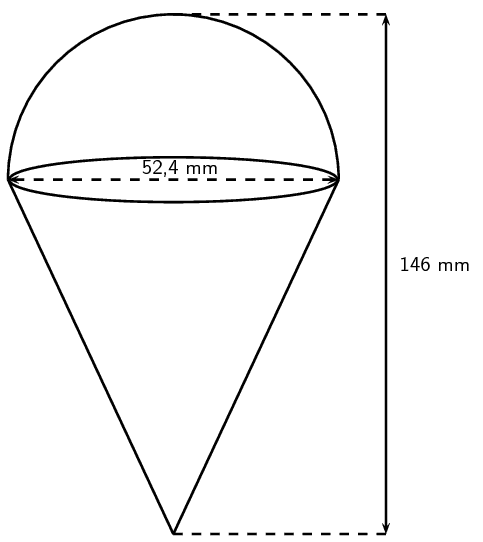
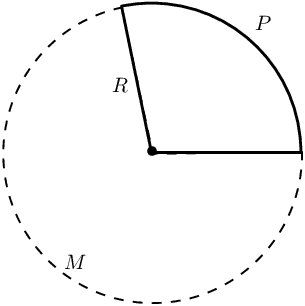7.3 Right pyramids, right cones and spheres | Measurement

7.4 Multiplying a dimension by a constant factor

7.3 Right pyramids, right cones and spheres (EMBHZ)

A pyramid is a geometric solid that has a polygon as its base and sides that converge at a point called the apex. In other words the sides are not perpendicular to the base.

The triangular pyramid and square pyramid take their names from the shape of their base. We call a pyramid a “right pyramid” if the line between the apex and the centre of the base is perpendicular to the base. Cones are similar to pyramids except that their bases are circles instead of polygons. Spheres are solids that are perfectly round and look the same from any direction.

Surface area of pyramids, cones and spheres (EMBJ2)

Square pyramid		$\begin{array}{r@{\;}c@{\;}l} \text{Surface area} &=& \text{area of base} \;+ \\ && \text{area of triangular sides} \\ &=& b^2 + \text{4}\left(\frac{1}{2}b{h}_{s}\right) \\ &=& b\left(b+2{h}_{s}\right) \end{array}$
Triangular pyramid		$\begin{array}{r@{\;}c@{\;}l} \text{Surface area} &= & \text{area of base} \;+ \\ && \text{area of triangular sides} \\ &=& \left(\frac{1}{2}b\times {h}_{b}\right)+3\left(\frac{1}{2}b\times {h}_{s}\right) \\ &=& \frac{1}{2}b\left({h}_{b}+3{h}_{s}\right) \end{array}$
Right cone		$\begin{array}{r@{\;}c@{\;}l} \text{Surface area} &=& \text{area of base} \;+ \\ && \text{area of walls} \\ &=& \pi {r}^{2}+\frac{1}{2}\times 2\pi rh \\ &=& \pi r\left(r+h\right) \end{array}$
Sphere		$\text{Surface area} = \text{4} \pi r^2$

temp text

Volume of pyramids, cones and spheres (EMBJ3)

Square pyramid		$\begin{array}{r@{\;}c@{\;}l} \text{Volume} &=& \frac{1}{3}\times \text{area of base} \;\times \\ && \text{height of pyramid} \\ &=& \frac{1}{3}\times {b}^{2}\times H \end{array}$
Triangular pyramid		$\begin{array}{r@{\;}c@{\;}l} \text{Volume} &=& \frac{1}{3}\times \text{area of base} \;\times \\ && \text{height of pyramid} \\ &=& \frac{1}{3}\times \frac{1}{2}bh\times H \end{array}$
Right cone		$\begin{array}{r@{\;}c@{\;}l} \text{Volume} &=& \frac{1}{3}\times \text{area of base} \;\times \\ && \text{height of cone} \\ &=& \frac{1}{3}\times \pi {r}^{2}\times H \end{array}$
Sphere		$\text{Volume}=\frac{4}{3}\pi {r}^{3}$

temp text

Video: 235K

Worked example 4: Finding surface area and volume

The Southern African Large Telescope (SALT) is housed in a cylindrical building with a domed roof in the shape of a hemisphere. The height of the building wall is $\text{17}$ $\text{m}$ and the diameter is $\text{26}$ $\text{m}$.

Calculate the total surface area of the building.
Calculate the total volume of the building.

Calculate the total surface area

\begin{align*} \text{Total surface area} &= \text{area of the dome} + \text{area of the cylinder} \\ \text{Surface area} &= \left[\frac{1}{2}(4 \pi r^2)\right] + \left[2 \pi r \times h\right] \\ &= \frac{1}{2}(4 \pi)(13)^2 + 2 \pi (\text{13})(\text{17}) \\ &= \text{2 450}\text{ m$^{2}$} \end{align*}

Calculate the total volume

\begin{align*} \text{Total volume} &= \text{volume of the dome} + \text{volume of the cylinder} \\ \text{Volume} &= \left[\frac{1}{2} \times \left( \frac{4}{3} \pi r^3 \right)\right] + \left[\pi r^2 h\right] \\ &= \frac{2}{3} \pi (\text{13})^3 + \pi (\text{11})^2 (\text{13}) \\ &= \text{9 543}\text{ m$^{3}$} \end{align*}

Finding surface area and volume

Textbook Exercise 7.4

Calculate the surface area of the ice-cream and the cone.

\begin{align*} \text{Radius }&=\frac{\text{52,4}}{2} \\ &=\text{26,2}\text{ mm} \\ \text{Height of cone }&= 146 - \text{26,2} \\ &=\text{119,8}\text{ mm} \end{align*}

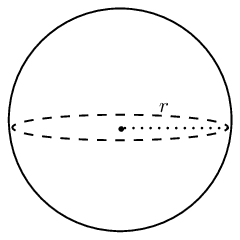
The surface area of the ice-cream is half a sphere:

\begin{align*} \text{Surface area ice-cream:} &=\dfrac{1}{2}(4 \pi r^{2}) \\ &= \dfrac{1}{2}(4 \times \pi \times (26,2)^{2}) \\ &\approx \text{4313,03 mm}^{2} \end{align*}

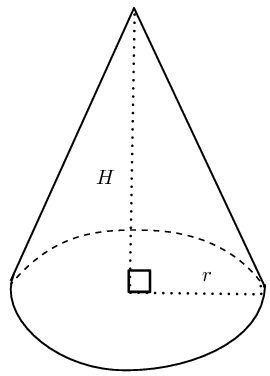
The surface area of the cone must not include the surface area of the circular face.

\begin{align*} \text{Surface area cone }&= \pi r(r + \sqrt{h^{2} + r^{2}}) - \pi r^{2} \\ &= \pi \times \text{26,2} \times (\text{26,2}+\sqrt{(119,8)^{2} + (26,2)^{2}}) - \pi \times (26,2)^{2} \\ &\approx \text{10093,76 mm}^{2} \\ \therefore \text{Surface area ice-cream and cone} &= \text{4313,03} + \text{10093,76} \\ &=\text{14406,79 mm}^{2} \\ &\approx \text{144,07}\text{ cm$^{2}$} \end{align*}

Calculate the total volume of the ice-cream and the cone.

\begin{align*} \text{Volume}&=\text{volume(cone)}+\text{volume}(\frac{1}{2}\text{sphere}) \\ &=\frac{1}{3}\pi r^2h+\frac{1}{2}\left(\frac{4}{3}\pi r^3\right) \\ &=\frac{1}{3}\pi(\text{26,2})^2\times\text{119,8}+\frac{2}{3}\pi(\text{26,2})^3 \\ &=\text{86 116,82}\ldots +\text{37 667,12}\ldots \\ &=\text{123 783,953}\ldots \text{ mm$^{3}$} \\ &\approx\text{124}\text{ cm$^{3}$} \end{align*}

How many ice-cream cones can be made from a $\text{5}$ $\text{ℓ}$ tub of ice-cream (assume the cone is completely filled with ice-cream)?

\begin{align*} \text{1 000}\text{ cm$^{3}$}&=\text{1}\text{ ℓ} \\ \therefore \text{5}\text{ ℓ}&= \text{5 000}\text{ cm$^{3}$}\\ \therefore \frac{\text{5 000}}{124} &\approx 40 \text{ cones} \end{align*}

Determine the value of $R$.

$R$ is the slant height.

\begin{align*} R &= \sqrt{r^{2} + h^{2}} \\ &= \sqrt{(\text{26,2})^{2} + (\text{119,8})^{2}} \\ &= \text{122,631}\ldots\text{ mm} \\ &\approx \text{123}\text{ mm} \end{align*}

Calculate the length of arc $P$.

\begin{align*} P &=\text{circumference of cone} \\ & = 2\pi(\text{26,2}) \\ &\approx \text{165}\text{ mm} \end{align*}

Determine the length of arc $M$.

\begin{align*} M&=2\pi(123)-165\\ &=\text{608}\text{ mm} \end{align*}

7.2 Right prisms and cylinders

Table of Contents

7.4 Multiplying a dimension by a constant factor

Square pyramid		\(\begin{array}{r@{\;}c@{\;}l} \text{Surface area} &=& \text{area of base} \;+ \\ && \text{area of triangular sides} \\ &=& b^2 + \text{4}\left(\frac{1}{2}b{h}_{s}\right) \\ &=& b\left(b+2{h}_{s}\right) \end{array}\)
Triangular pyramid		\(\begin{array}{r@{\;}c@{\;}l} \text{Surface area} &= & \text{area of base} \;+ \\ && \text{area of triangular sides} \\ &=& \left(\frac{1}{2}b\times {h}_{b}\right)+3\left(\frac{1}{2}b\times {h}_{s}\right) \\ &=& \frac{1}{2}b\left({h}_{b}+3{h}_{s}\right) \end{array}\)
Right cone		\(\begin{array}{r@{\;}c@{\;}l} \text{Surface area} &=& \text{area of base} \;+ \\ && \text{area of walls} \\ &=& \pi {r}^{2}+\frac{1}{2}\times 2\pi rh \\ &=& \pi r\left(r+h\right) \end{array}\)
Sphere		\(\text{Surface area} = \text{4} \pi r^2\)

Square pyramid		\(\begin{array}{r@{\;}c@{\;}l} \text{Volume} &=& \frac{1}{3}\times \text{area of base} \;\times \\ && \text{height of pyramid} \\ &=& \frac{1}{3}\times {b}^{2}\times H \end{array}\)
Triangular pyramid		\(\begin{array}{r@{\;}c@{\;}l} \text{Volume} &=& \frac{1}{3}\times \text{area of base} \;\times \\ && \text{height of pyramid} \\ &=& \frac{1}{3}\times \frac{1}{2}bh\times H \end{array}\)
Right cone		\(\begin{array}{r@{\;}c@{\;}l} \text{Volume} &=& \frac{1}{3}\times \text{area of base} \;\times \\ && \text{height of cone} \\ &=& \frac{1}{3}\times \pi {r}^{2}\times H \end{array}\)
Sphere		\(\text{Volume}=\frac{4}{3}\pi {r}^{3}\)