7.1 Area of a polygon
|
Previous
End of chapter exercises
|
Next
7.2 Right prisms and cylinders
|
Chapter 7: Measurement
- Use paper or cardboard for the net of solids to help learners see the different heights, particularly perpendicular and slanted heights.
- Units are compulsory when working with real life contexts.
- Sketches are valuable and important tools.
- Rounding off should only be done in the last step and level of accuracy should be relevant to the context.
This chapter is a revision of perimeters and areas of two dimensional objects and volumes of three dimensional objects. We also examine different combinations of geometric objects and calculate areas and volumes in a variety of real-life contexts.
7.1 Area of a polygon (EMBHV)
|
Square |
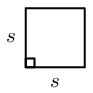 |
\(\text{Area}={s}^{2}\) |
|
Rectangle |
 |
\(\text{Area}=b\times h\) |
|
Triangle |
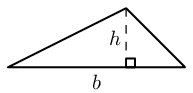 |
\(\text{Area}=\frac{1}{2}b\times h\) |
|
Trapezium |
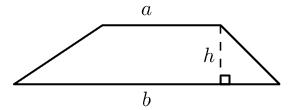 |
\(\text{Area}=\frac{1}{2}\left(a+b\right)\times h\) |
|
Parallelogram |
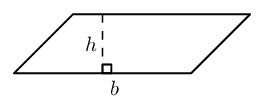 |
\(\text{Area}=b\times h\) |
|
Circle |
 |
\(\text{Area}=\pi {r}^{2}\) \(\left(\text{Circumference}=2\pi r\right)\) |
Worked example 1: Finding the area of a polygon
\(ABCD\) is a parallelogram with \(DC = \text{15}\text{ cm}\), \(h = \text{8}\text{ cm}\) and \(BF = \text{9}\text{ cm}\).
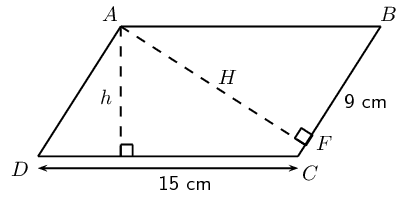
Calculate:
- the area of \(ABCD\)
- the perimeter of \(ABCD\)
Determine the area
The area of a parallelogram \(ABCD =\) base \(\times\) height:
\begin{align*} \text{Area} &= \text{15} \times \text{8} \\ &= \text{120}\text{ cm$^{2}$} \end{align*}Determine the perimeter
The perimeter of a parallelogram \(ABCD = 2DC + 2BC\).
To find the length of \(BC\), we use \(AF \perp BC\) and the theorem of Pythagoras.
\begin{align*} \text{In } \triangle \text{ ABF:} \quad AF^2 &= AB^2 - BF^2 \\ &= \text{15}^2 - \text{9}^2 \\ &= \text{144} \\ \therefore AF &= \text{12}\text{ cm} \end{align*}\begin{align*} \text{Area} ABCD &= BC \ \times AF \\ \text{120} &= BC \times \text{12} \\ \therefore BC &= \text{10}\text{ cm} \end{align*}\begin{align*} \therefore \text{Perimeter} ABCD &=2(\text{15})+2(\text{10}) \\ &= \text{50}\text{ cm} \end{align*}Area of a polygon
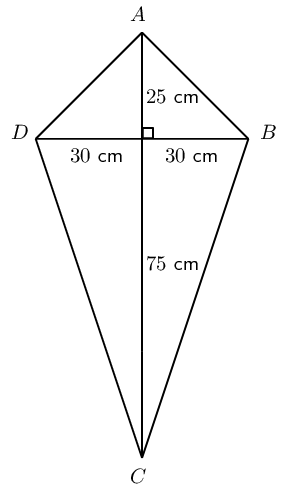
Vuyo and Banele are having a competition to see who can build the best kite using balsa wood (a lightweight wood) and paper. Vuyo decides to make his kite with one diagonal \(\text{1}\) \(\text{m}\) long and the other diagonal \(\text{60}\) \(\text{cm}\) long. The intersection of the two diagonals cuts the longer diagonal in the ratio \(\text{1}:\text{3}\).
Banele also uses diagonals of length \(\text{60}\) \(\text{cm}\) and \(\text{1}\) \(\text{m}\), but he designs his kite to be rhombus-shaped.

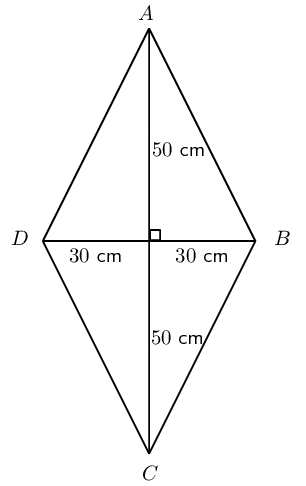
Same amount of paper is required for both designs. Vuyo's designs uses more balsa wood.
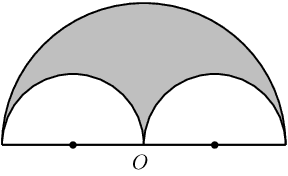
\(O\) is the centre of the bigger semi-circle with a radius of \(\text{10}\) \(\text{units}\). Two smaller semi-circles are inscribed into the bigger one, as shown on the diagram. Calculate the following (in terms of \(\pi\)):
Karen's engineering textbook is \(\text{30}\) \(\text{cm}\) long and \(\text{20}\) \(\text{cm}\) wide. She notices that the dimensions of her desk are in the same proportion as the dimensions of her textbook.
If the desk is \(\text{90}\text{ cm}\) wide, calculate the area of the top of the desk.
Karen uses some cardboard to cover each corner of her desk with an isosceles triangle, as shown in the diagram:
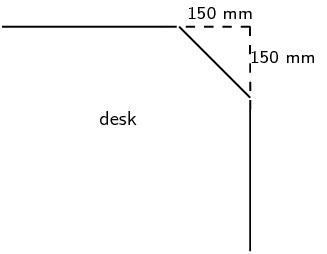
Calculate the new perimeter and area of the visible part of the top of her desk.
|
Previous
End of chapter exercises
|
Table of Contents |
Next
7.2 Right prisms and cylinders
|
