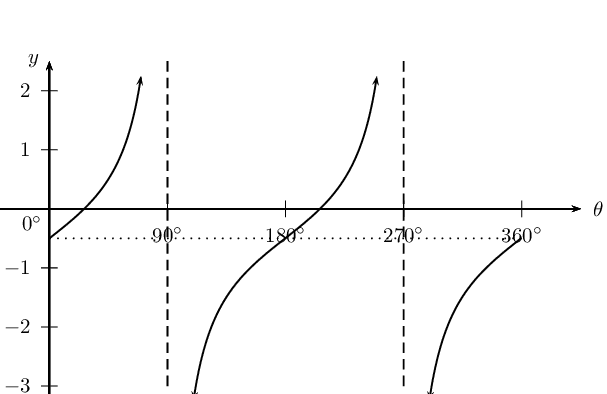
\(y_1 = \tan \theta - \frac{1}{2}\)
|
Previous
5.6 The cosine function
|
Next
5.8 Summary
|
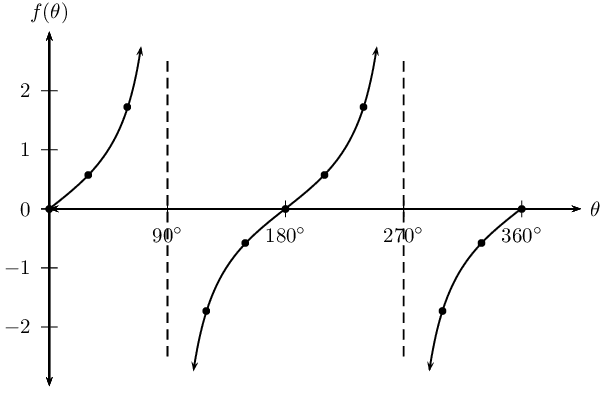
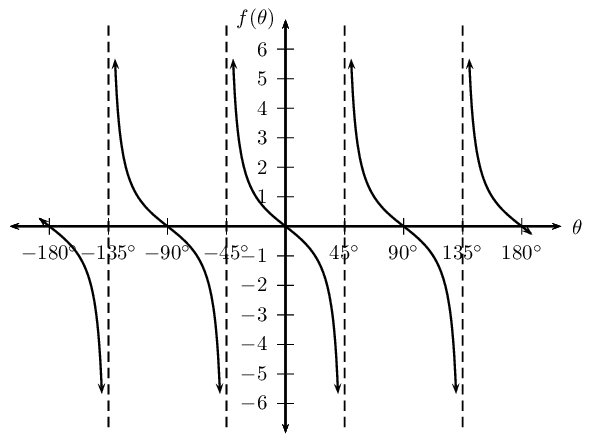
The dashed vertical lines are called the asymptotes. The asymptotes are at the values of θ where \(\tan\theta\) is not defined.
Period: \(\text{180}\text{°}\)
Domain: \(\left\{\theta : \text{0}\text{°} \le \theta \le \text{360}\text{°}, \theta \ne \text{90}\text{°}; \text{270}\text{°}\right\}\)
Range: \(\left\{f(\theta):f(\theta)\in ℝ\right\}\)
\(x\)-intercepts: \(\left(\text{0}\text{°};0\right)\), \(\left(\text{180}\text{°};0\right)\), \(\left(\text{360}\text{°};0\right)\)
\(y\)-intercept: \(\left(\text{0}\text{°};0\right)\)
Asymptotes: the lines \(\theta =\text{90}\text{°}\) and \(\theta =\text{270}\text{°}\)
Tangent functions of the general form \(y = a \tan \theta + q\), where \(a\) and \(q\) are constants.
The effects of \(a\) and \(q\) on \(f(\theta) = a \tan \theta + q\):
The effect of \(q\) on vertical shift
For \(q>0\), \(f(\theta)\) is shifted vertically upwards by \(q\) units.
For \(q<0\), \(f(\theta)\) is shifted vertically downwards by \(q\) units.
The effect of \(a\) on shape
For \(a>1\), branches of \(f(\theta)\) are steeper.
For \(0<a<1\), branches of \(f(\theta)\) are less steep and curve more.
For \(a<0\), there is a reflection about the \(x\)-axis.
For \(-1 < a < 0\), there is a reflection about the \(x\)-axis and the branches of the graph are less steep.
For \(a < -1\), there is a reflection about the \(x\)-axis and the branches of the graph are steeper.
|
\(a<0\) |
\(a>0\) |
|
|
\(q>0\) |
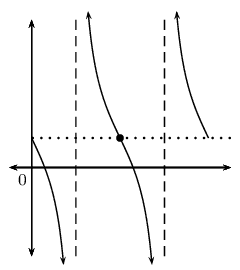 |
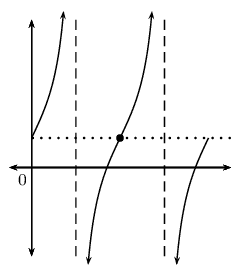 |
|
\(q=0\) |
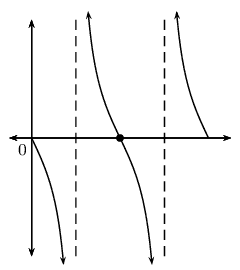 |
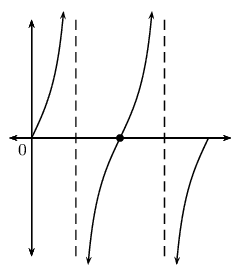 |
|
\(q<0\) |
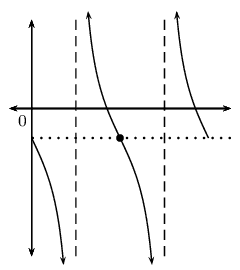 |
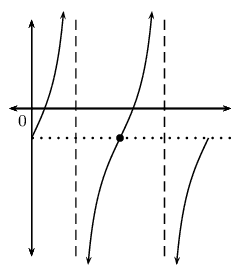 |
On separate axes, accurately draw each of the following functions for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\):
For each function determine the following:
\(y_1 = \tan \theta - \frac{1}{2}\)

\(y_2 = - 3 \tan \theta\)
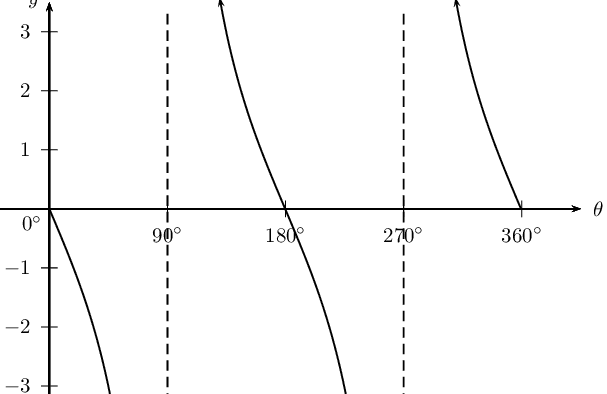
\(y_3 = \tan \theta + 2\)
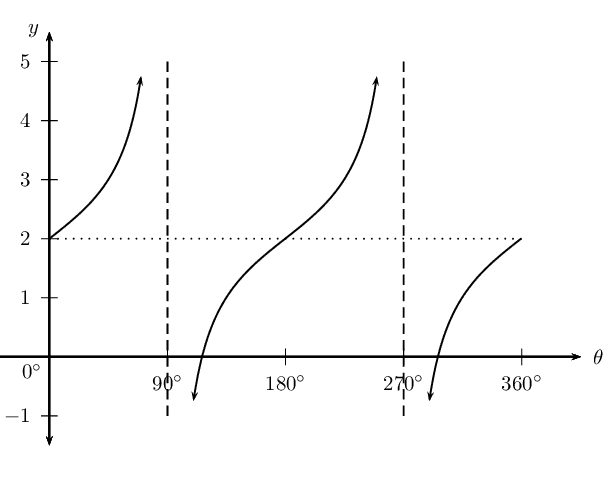
\(y_4 = 2 \tan \theta - 1\)
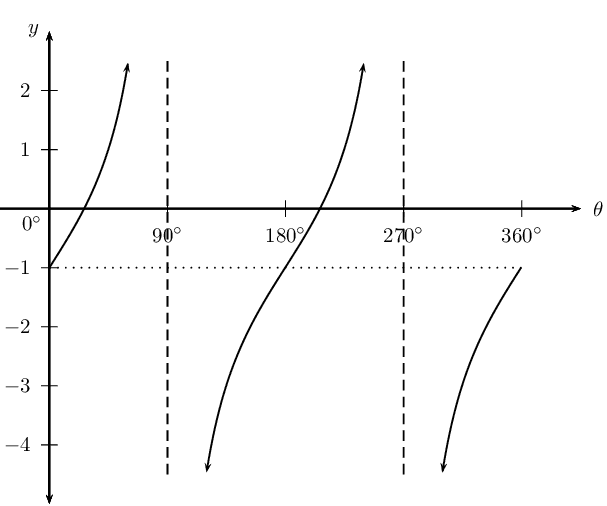
| θ | \(-\text{360}\)\(\text{°}\) | \(-\text{300}\)\(\text{°}\) | \(-\text{240}\)\(\text{°}\) | \(-\text{180}\)\(\text{°}\) | \(-\text{120}\)\(\text{°}\) | \(-\text{60}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) |
| \(\tan \theta\) | |||||||
| θ | \(\text{60}\)\(\text{°}\) | \(\text{120}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) | \(\text{240}\)\(\text{°}\) | \(\text{300}\)\(\text{°}\) | \(\text{360}\)\(\text{°}\) | |
| \(\tan \theta\) |
Use the table of values to plot the graph of \(y_1 = \tan \theta\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\).
On the same system of axes, plot the following graphs:
Use your sketches of the functions above to complete the following table:
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| period | ||||
| domain | ||||
| range | ||||
| \(y\)-intercept(s) | ||||
| \(x\)-intercept(s) | ||||
| asymptotes | ||||
| effect of \(k\) |
What do you notice about \(y_1 = \tan \theta\) and \(y_2 = \tan (-\theta)\)?
Is \(\tan (-\theta) = -\tan \theta\) a true statement? Explain your answer.
The effect of the parameter on \(y = \tan k\theta\)
The value of \(k\) affects the period of the tangent function. If \(k\) is negative, then the graph is reflected about the \(y\)-axis.
For \(k > 0\):
For \(k > 1\), the period of the tangent function decreases.
For \(0 < k < 1\), the period of the tangent function increases.
For \(k < 0\):
For \(-1 < k < 0\), the graph is reflected about the \(y\)-axis and the period increases.
For \(k < -1\), the graph is reflected about the \(y\)-axis and the period decreases.
Negative angles: \[\tan (-\theta) = -\tan \theta\]
Calculating the period:
To determine the period of \(y = \tan k\theta\) we use, \[\text{Period} = \frac{\text{180}\text{°}}{|k|}\] where \(|k|\) is the absolute value of \(k\).
|
\(k > 0\) |
\(k < 0\) |
 |
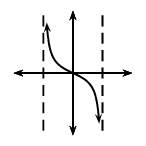 |
For each function determine the following:
Notice that \(k > 1\) for \(y_2 = \tan \frac{3\theta}{2}\), therefore the period of the graph decreases.
| θ | \(-\text{180}\)\(\text{°}\) | \(-\text{135}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(-\text{45}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{45}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{135}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) |
| \(\tan \theta\) | \(\text{0}\) | \(\text{1}\) | undef | \(-\text{1}\) | \(\text{0}\) | \(\text{1}\) | undef | \(-\text{1}\) | \(\text{0}\) |
| \(\tan \frac{3\theta}{2}\) | undef | \(-\text{0,41}\) | \(\text{1}\) | \(-\text{2,41}\) | \(\text{0}\) | \(\text{2,41}\) | \(-\text{1}\) | \(\text{0,41}\) | undef |
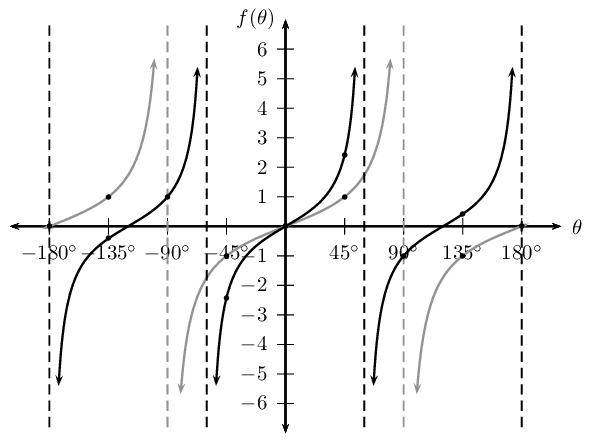
| \(y_1 = \tan \theta\) | \(y_2 = \tan \frac{3\theta}{2}\) | |
| period | \(\text{180}\)\(\text{°}\) | \(\text{120}\)\(\text{°}\) |
| domain | \(\{\theta: -\text{180}\text{°} \leq \theta \leq \text{180}\text{°}, \theta \ne -\text{90}\text{°}; \text{90}\text{°}\}\) | \(\{\theta: -\text{180}\text{°} < \theta < \text{180}\text{°}, \theta \ne -\text{60}\text{°}; \text{60}\text{°}\}\) |
| range | \(\{f(\theta): f(\theta) \in \mathbb{R}\}\) | \(\{f(\theta): f(\theta) \in \mathbb{R}\}\) |
| \(y\)-intercept(s) | \((\text{0}\text{°};0)\) | \((\text{0}\text{°};0)\) |
| \(x\)-intercept(s) | \((-\text{180}\text{°};0)\), \((\text{0}\text{°};0)\) and \((\text{180}\text{°};0)\) | \((-\text{120}\text{°};0)\), \((\text{0}\text{°};0)\) and \((\text{120}\text{°};0)\) |
| asymptotes | \(\theta = -\text{90}\text{°}\) and \(\theta = \text{90}\text{°}\) | \(\theta = -\text{180}\text{°}\); \(-\text{60}\text{°}\) and \(\text{180}\text{°}\) |
For functions of the general form: \(f(\theta) = y =\tan k\theta\):
Domain and range
The domain of one branch is \(\{ \theta: -\frac{\text{90}\text{°}}{k} < \theta < \frac{\text{90}\text{°}}{k}, \theta \in \mathbb{R}\}\) because \(f(\theta)\) is undefined for \(\theta = -\frac{\text{90}\text{°}}{k}\) and \(\theta = \frac{\text{90}\text{°}}{k}\).
The range is \(\{ f(\theta): f(\theta) \in \mathbb{R} \}\) or \((-\infty; \infty)\).
Intercepts
The \(x\)-intercepts are determined by letting \(f(\theta) = 0\) and solving for \(\theta\).
The \(y\)-intercept is calculated by letting \(\theta = 0\) and solving for \(f(\theta)\). \begin{align*} y &= \tan k\theta \\ &= \tan \text{0}\text{°} \\ &= 0 \end{align*} This gives the point \((\text{0}\text{°};0)\).
Asymptotes
These are the values of \(k\theta\) for which \(\tan k\theta\) is undefined.
Sketch the following functions for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\). For each graph determine:
\(f(\theta) =\tan 2\theta\)
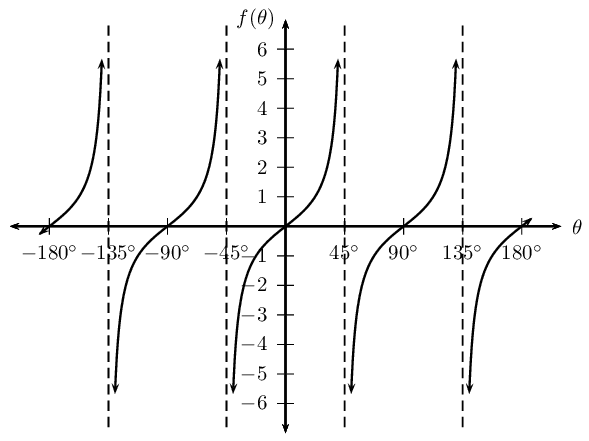
\(g(\theta) =\tan \frac{3\theta}{4}\)
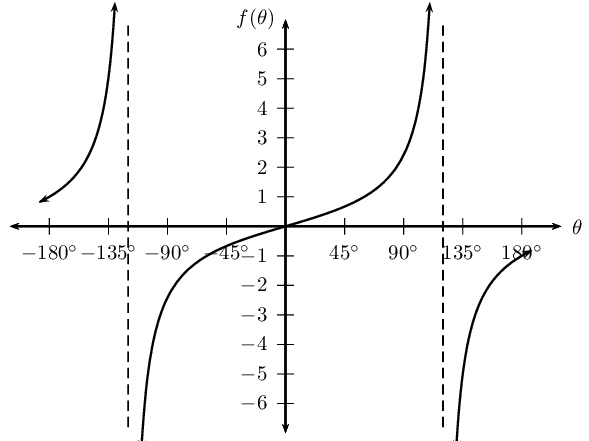
\(h(\theta) =\tan (-2\theta)\)
\(k(\theta) =\tan \frac{2\theta}{3}\)
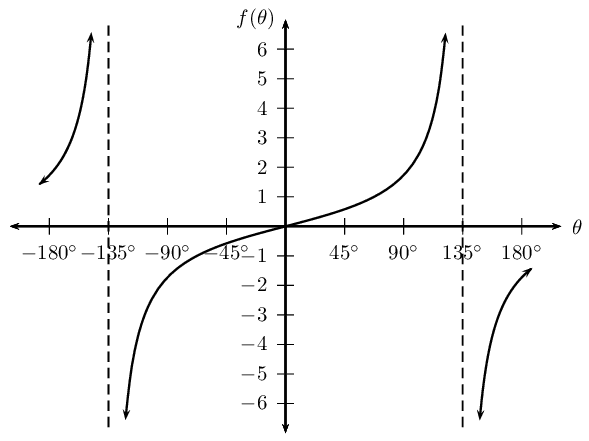
We now consider tangent functions of the form \(y = \tan(\theta + p)\) and the effects of parameter \(p\).
On the same system of axes, plot the following graphs for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\):
Use your sketches of the functions above to complete the following table:
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | \(y_5\) | |
| period | |||||
| domain | |||||
| range | |||||
| \(y\)-intercept(s) | |||||
| \(x\)-intercept(s) | |||||
| asymptotes | |||||
| effect of \(p\) |
The effect of the parameter on \(y = \tan(\theta + p)\)
The effect of \(p\) on the tangent function is a horizontal shift (or phase shift); the entire graph slides to the left or to the right.
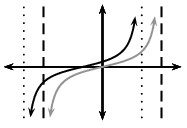
For \(p > 0\), the graph of the tangent function shifts to the left by \(p\).
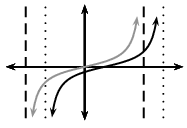
For \(p < 0\), the graph of the tangent function shifts to the right by \(p\).
| \(p > 0\) | \(p < 0\) |
 |
 |
For each function determine the following:
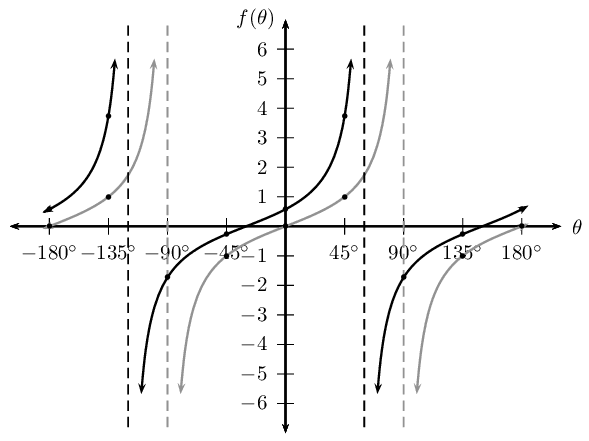
Notice that for \(y_1 = \tan \theta\) we have \(p = \text{0}\text{°}\) (no phase shift) and for \(y_2 = \tan (\theta + \text{30}\text{°})\) we have \(p = \text{30}\text{°} > 0\) and therefore the graph shifts to the left by \(\text{30}\)\(\text{°}\).
| θ | \(-\text{180}\)\(\text{°}\) | \(-\text{135}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(-\text{45}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{45}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{135}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) |
| \(\tan \theta\) | \(\text{0}\) | \(\text{1}\) | undef | \(-\text{1}\) | \(\text{0}\) | \(\text{1}\) | undef | \(-\text{1}\) | \(\text{0}\) |
| \(\tan (\theta + \text{30}\text{°})\) | \(\text{0,58}\) | \(\text{3,73}\) | \(-\text{1,73}\) | \(-\text{0,27}\) | \(\text{0,58}\) | \(\text{3,73}\) | \(-\text{1,73}\) | \(-\text{0,27}\) | \(\text{0,58}\) |
| \(y_1 = \tan \theta\) | \(y_2 = \tan (\theta + \text{30}\text{°})\) | |
| period | \(\text{180}\text{°}\) | \(\text{180}\text{°}\) |
| domain | \(\{ \theta: -\text{180}\text{°} \leq \theta \leq \text{180}\text{°}, \theta \ne -\text{90}\text{°}; \text{90}\text{°} \}\) | \(\{ \theta: -\text{180}\text{°} \leq \theta \leq \text{180}\text{°}, \theta \ne -\text{120}\text{°}; \text{60}\text{°} \}\) |
| range | \((-\infty;\infty)\) | \((-\infty;\infty)\) |
| \(y\)-intercept(s) | \((\text{0}\text{°};0)\) | \((\text{0}\text{°};\text{0,58})\) |
| \(x\)-intercept(s) | \((-\text{180}\text{°};0)\), \((\text{0}\text{°};0)\) and \((\text{180}\text{°};0)\) | \((-\text{30}\text{°};0) \text{ and } (\text{150}\text{°};0)\) |
| asymptotes | \(\theta = -\text{90}\text{°} \text{ and } \theta = \text{90}\text{°}\) | \(\theta = -\text{120}\text{°} \text{ and } \theta = \text{60}\text{°}\) |
For functions of the general form: \(f(\theta) = y =\tan (\theta + p)\):
Domain and range
The domain of one branch is \(\{ \theta: \theta \in (-\text{90}\text{°} - p; \text{90}\text{°} - p) \}\) because the function is undefined for \(\theta = -\text{90}\text{°} - p\) and \(\theta = \text{90}\text{°} - p\).
The range is \(\{ f(\theta): f(\theta) \in \mathbb{R} \}\).
Intercepts
The \(x\)-intercepts are determined by letting \(f(\theta) = 0\) and solving for \(\theta\).
The \(y\)-intercept is calculated by letting \(\theta = \text{0}\text{°}\) and solving for \(f(\theta)\). \begin{align*} y &= \tan (\theta + p) \\ &= \tan (\text{0}\text{°} + p) \\ &= \tan p \end{align*} This gives the point \((\text{0}\text{°};\tan p)\).
Sketch the following functions for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\).
For each function, determine the following:
\(f(\theta) =\tan (\theta + \text{45}\text{°})\)
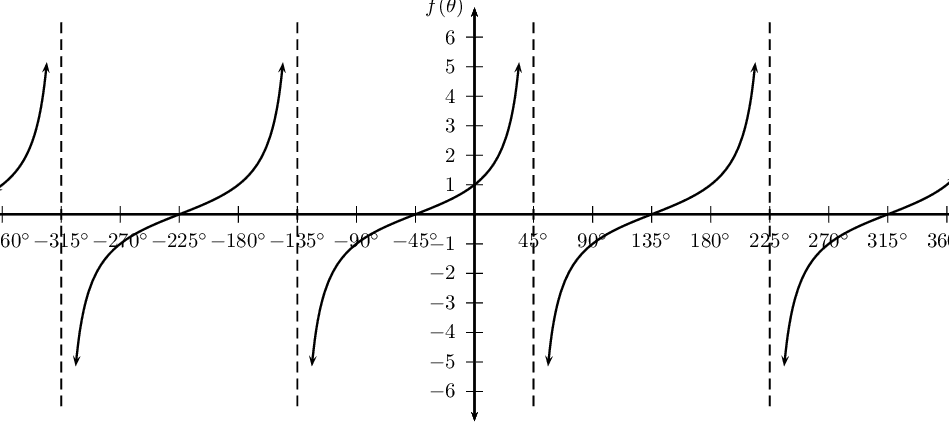
\(g(\theta) =\tan (\theta - \text{30}\text{°})\)
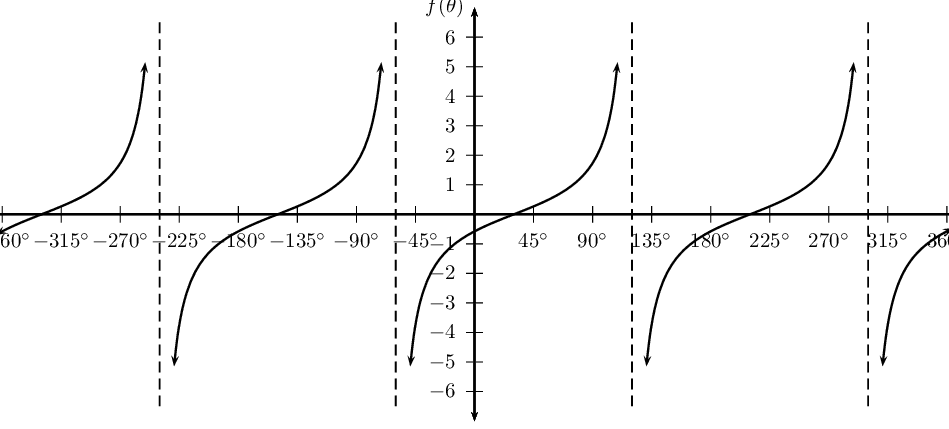
\(h(\theta) =\tan (\theta + \text{60}\text{°})\)
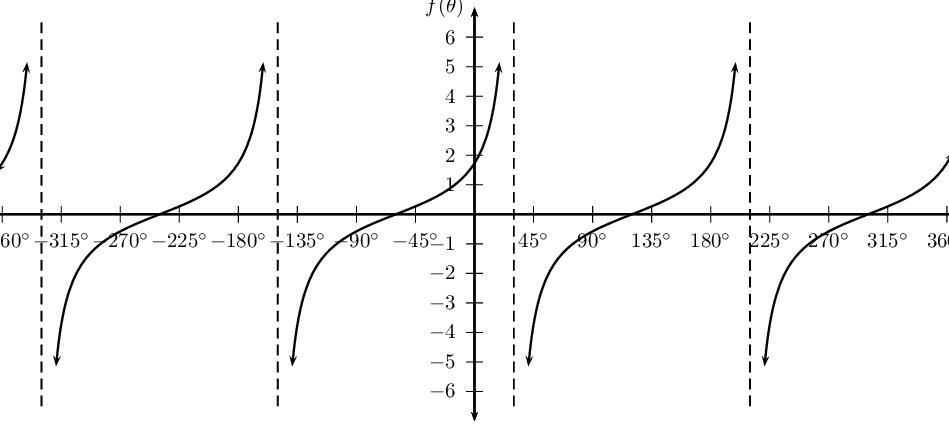
Sketch the graph of \(f(\theta) = \tan \frac{1}{2}(\theta - \text{30}\text{°})\) for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\).
From the equation we see that \(0 < k < 1\), therefore the branches of the graph will be less steep than the standard tangent graph \(y = \tan \theta\). We also notice that \(p < 0\) so the graph will be shifted to the right on the \(x\)-axis.
The period for \(f(\theta) = \tan \frac{1}{2}(\theta - \text{30}\text{°})\) is:
\begin{align*} \text{Period} &= \frac{\text{180}\text{°}}{|k|} \\ &= \dfrac{\text{180}\text{°}}{\frac{1}{2}} \\ &= \text{360}\text{°} \end{align*}The standard tangent graph, \(y = \tan \theta\), for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\) is undefined at \(\theta = -\text{90}\text{°}\) and \(\theta = \text{90}\text{°}\). Therefore we can determine the asymptotes of \(f(\theta) = \tan \frac{1}{2}(\theta - \text{30}\text{°})\):
The asymptote at \(\theta = \text{210}\text{°}\) lies outside the required interval.
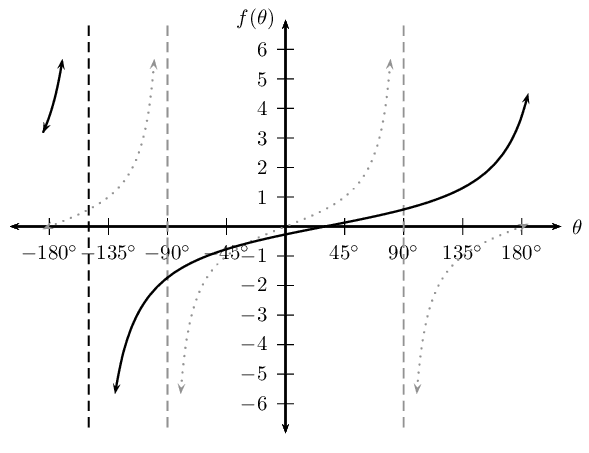
Period: \(\text{360}\text{°}\)
Domain: \(\{ \theta: -\text{180}\text{°} \leq \theta \leq \text{180}\text{°}, \theta \ne -\text{150}\text{°} \}\)
Range: \((-\infty;\infty)\)
\(y\)-intercepts: \((\text{0}\text{°};-\text{0,27})\)
\(x\)-intercept: \((\text{30}\text{°};0)\)
Asymptotes: \(\theta = -\text{150}\text{°}\)
Sketch the following graphs on separate axes:
\(y = \tan \theta - 1\) for \(-\text{90}\text{°} \leq \theta \leq \text{90}\text{°}\)
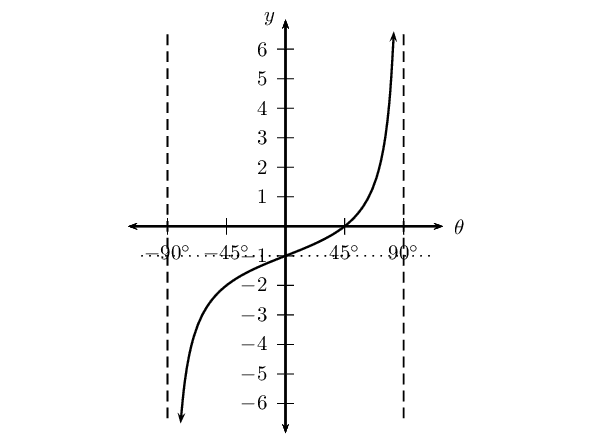
\(f(\theta) = -\tan 2\theta\) for \(\text{0}\text{°} \leq \theta \leq \text{90}\text{°}\)
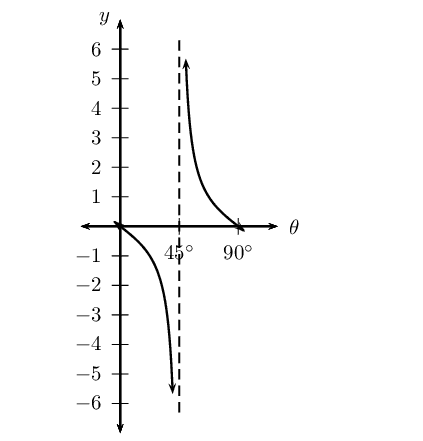
\(y = \frac{1}{2} \tan (\theta + \text{45}\text{°})\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
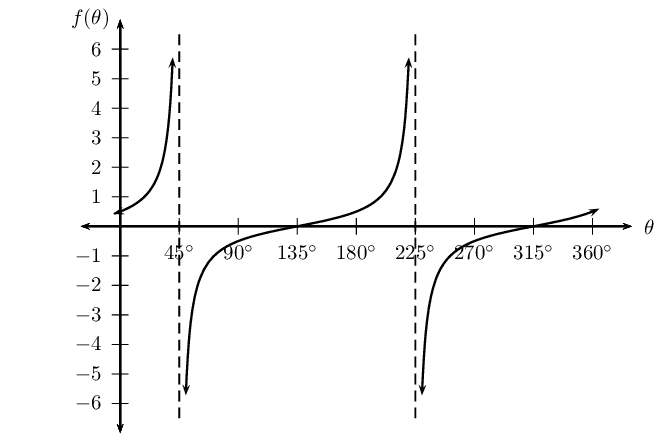
\(y = \tan (30° - \theta)\) for \(-180° \leq \theta \leq 180° \)
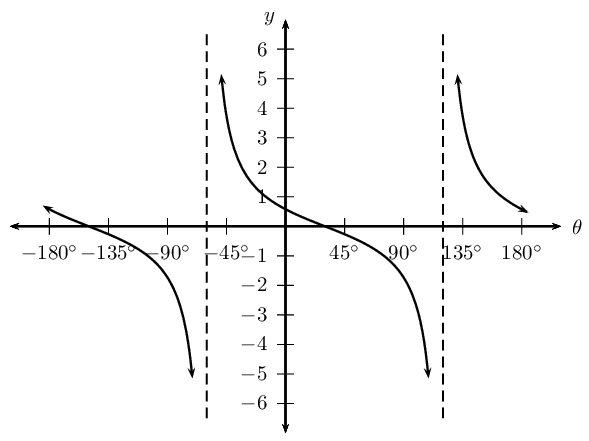
Given the graph of \(y = a \tan k\theta\), determine the values of \(a\) and \(k\).
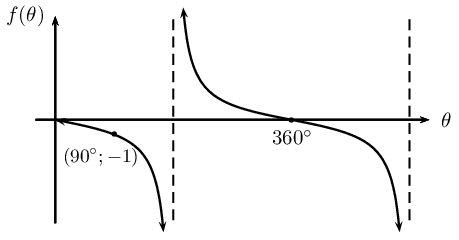
Determine the equation for each of the following:
\(f(\theta) = a \sin k\theta\) and \(g(\theta) = a \tan \theta\)
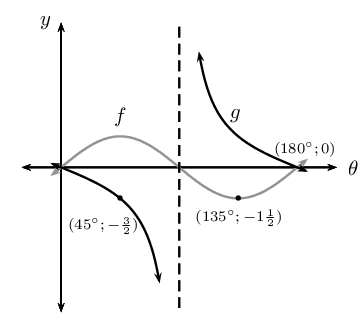
\(f(\theta) = a \sin k\theta\) and \(g(\theta) = a \cos ( \theta + p)\)
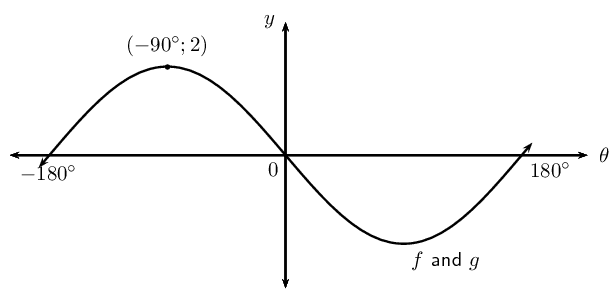
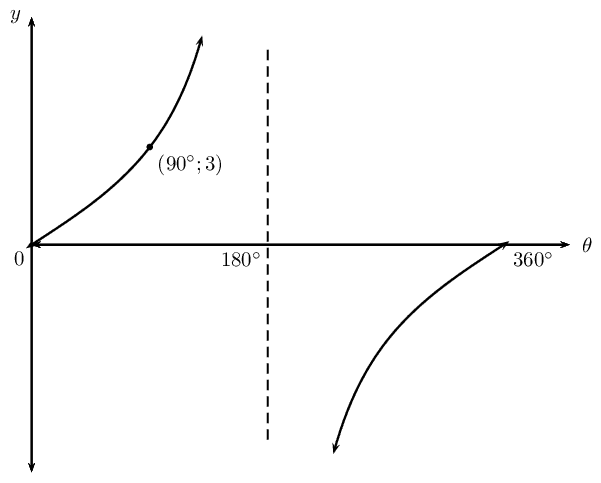
\(y = a \tan k\theta\)
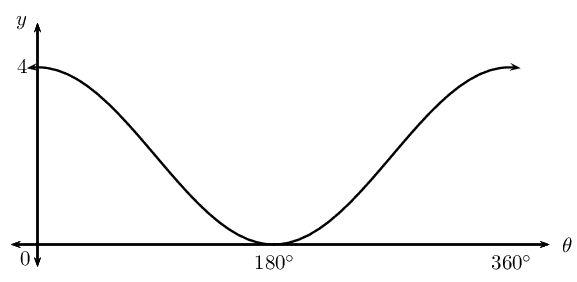
\(y = a \cos \theta + q\)
Given the functions \(f(\theta) = 2 \sin \theta\) and \(g(\theta) = \cos \theta + 1\):
Sketch the graphs of both functions on the same system of axes, for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\). Indicate the turning points and intercepts on the diagram.
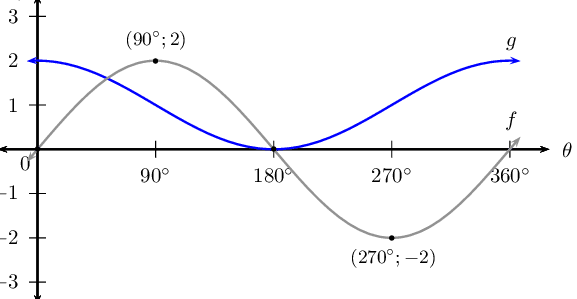
What is the period of \(f\)?
What is the amplitude of \(g\)?
Use your sketch to determine how many solutions there are for the equation \(2 \sin \theta - \cos \theta = 1\). Give one of the solutions.
Indicate on your sketch where on the graph the solution to \(2 \sin \theta = -1\) is found.
The sketch shows the two functions \(f(\theta) = a \cos \theta\) and \(g(\theta) = \tan \theta\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\). Points \(P(\text{135}\text{°}; b)\) and \(Q(c; -1)\) lie on \(g(\theta)\) and \(f(\theta)\) respectively.
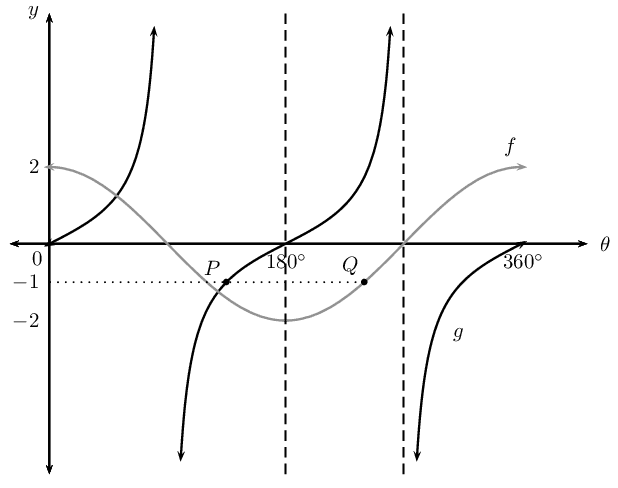
Determine the values of \(a\), \(b\) and \(c\).
What is the period of \(g\)?
Solve the equation \(\cos \theta = \frac{1}{2}\) graphically and show your answer(s) on the diagram.
Determine the equation of the new graph if \(g\) is reflected about the \(x\)-axis and shifted to the right by \(\text{45}\text{°}\).
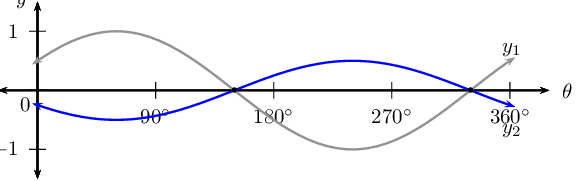
Sketch the graphs of \(y_1 = -\frac{1}{2} \sin (\theta + \text{30}\text{°})\) and \(y_2 = \cos (\theta - \text{60}\text{°})\), on the same system of axes for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\).
|
Previous
5.6 The cosine function
|
Table of Contents |
Next
5.8 Summary
|