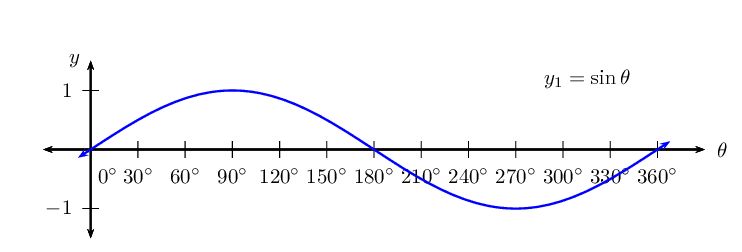
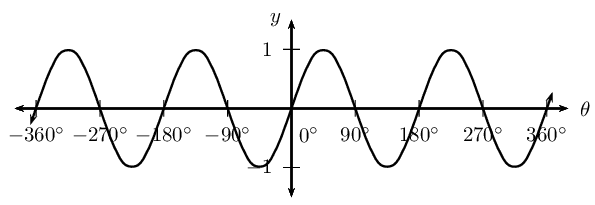
\(y_1 = \sin \theta\)
|
Previous
5.4 Exponential functions
|
Next
5.6 The cosine function
|
Period of one complete wave is \(\text{360}\)\(\text{°}\).
Amplitude is the maximum height of the wave above and below the \(x\)-axis and is always positive. Amplitude = \(\text{1}\).
Domain: \([\text{0}\text{°};\text{360}\text{°}]\)
For \(y = \sin \theta\), the domain is \(\{ \theta: \theta \in \mathbb{R} \}\), however in this case, the domain has been restricted to the interval \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\).
Range: \(\left[-1;1\right]\)
\(x\)-intercepts: \(\left(\text{0}\text{°};0\right)\), \(\left(\text{180}\text{°};0\right)\), \(\left(\text{360}\text{°};0\right)\)
\(y\)-intercept: \(\left(\text{0}\text{°};0\right)\)
Maximum turning point: \(\left(\text{90}\text{°};1\right)\)
Minimum turning point: \(\left(\text{270}\text{°};-1\right)\)
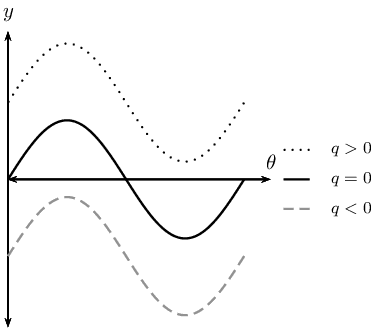
The effects of \(a\) and \(q\) on \(f(\theta) = a \sin \theta + q\):
The effect of \(q\) on vertical shift
For \(q>0\), \(f(\theta)\) is shifted vertically upwards by \(q\) units.
For \(q<0\), \(f(\theta)\) is shifted vertically downwards by \(q\) units.
The effect of \(a\) on shape
For \(a>1\), the amplitude of \(f(\theta)\) increases.
For \(0<a<1\), the amplitude of \(f(\theta)\) decreases.
For \(a<0\), there is a reflection about the \(x\)-axis.
For \(-1 < a < 0\), there is a reflection about the \(x\)-axis and the amplitude decreases.
For \(a < -1\), there is a reflection about the \(x\)-axis and the amplitude increases.
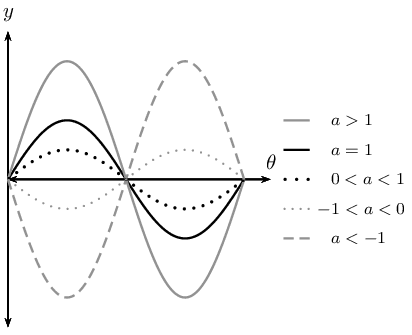
On separate axes, accurately draw each of the following functions for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\).
For each function also determine the following:
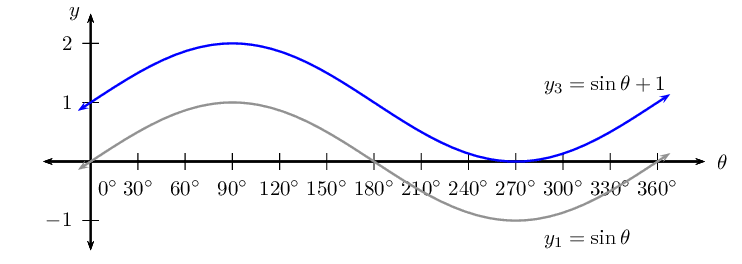
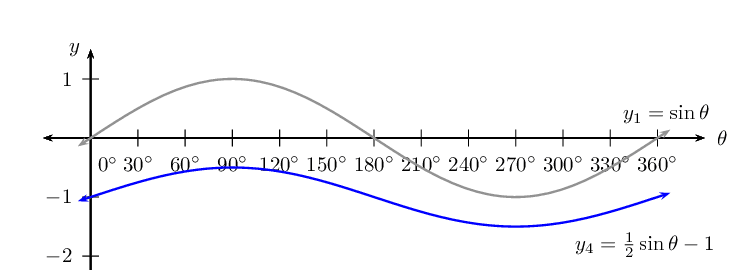
\(y_1 = \sin \theta\)

\(y_2 = - 2 \sin \theta\)
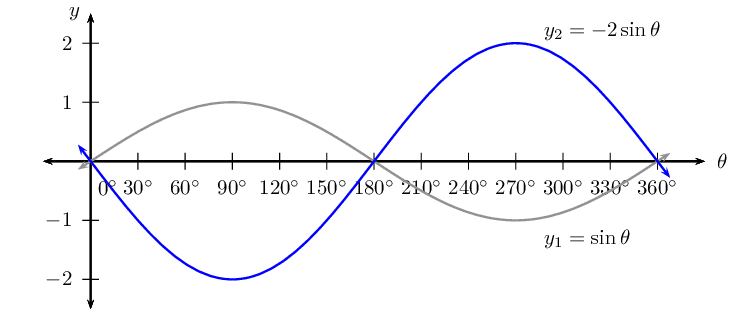
\(y_3 = \sin \theta + 1\)
\(y_4 = \frac{1}{2} \sin \theta - 1\)
| \(θ\) | \(-\text{360}\)\(\text{°}\) | \(-\text{270}\)\(\text{°}\) | \(-\text{180}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) | \(\text{270}\)\(\text{°}\) | \(\text{360}\)\(\text{°}\) |
| \(\sin \theta\) |
Use the table of values to plot the graph of \(y_1 = \sin \theta\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\).
On the same system of axes, plot the following graphs:
Use your sketches of the functions above to complete the following table:
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| period | ||||
| amplitude | ||||
| domain | ||||
| range | ||||
| maximum turning points | ||||
| minimum turning points | ||||
| \(y\)-intercept(s) | ||||
| \(x\)-intercept(s) | ||||
| effect of \(k\) |
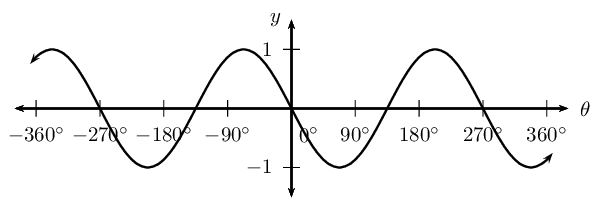
What do you notice about \(y_1 = \sin \theta\) and \(y_2 = \sin (-\theta)\)?
Is \(\sin (-\theta) = -\sin \theta\) a true statement? Explain your answer.
The effect of the parameter on \(y = \sin k\theta\)
The value of \(k\) affects the period of the sine function. If \(k\) is negative, then the graph is reflected about the \(y\)-axis.
For \(k > 0\):
For \(k > 1\), the period of the sine function decreases.
For \(0 < k < 1\), the period of the sine function increases.
For \(k < 0\):
For \(-1 < k < 0\), the graph is reflected about the \(y\)-axis and the period increases.
For \(k < -1\), the graph is reflected about the \(y\)-axis and the period decreases.
Negative angles: \[\sin (-\theta) = -\sin \theta\]
Calculating the period:
To determine the period of \(y = \sin k\theta\) we use, \[\text{Period } = \frac{\text{360}\text{°}}{|k|}\] where \(|k|\) is the absolute value of \(k\) (this means that \(k\) is always considered to be positive).
|
\(0 < k < 1\) |
\(-1 < k < 0\) |
 |
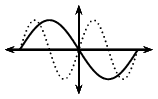 |
|
\(k > 1\) |
\(k < -1\) |
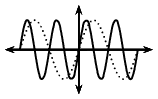 |
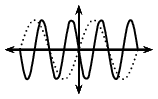 |
For each function determine the following:
Notice that \(k > 1\) for \(y_2 = \sin \frac{3\theta}{2}\), therefore the period of the graph decreases.
| \(θ\) | \(-\text{180}\)\(\text{°}\) | \(-\text{135}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(-\text{45}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{45}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{135}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) |
| \(\sin \theta\) | \(\text{0}\) | \(-\text{0,71}\) | \(-\text{1}\) | \(-\text{0,71}\) | \(\text{0}\) | \(\text{0,71}\) | \(\text{1}\) | \(\text{0,71}\) | \(\text{0}\) |
| \(\sin \frac{3\theta}{2}\) | \(\text{1}\) | \(\text{0,38}\) | \(-\text{0,71}\) | \(-\text{0,92}\) | \(\text{0}\) | \(\text{0,92}\) | \(\text{0,71}\) | \(-\text{0,38}\) | \(-\text{1}\) |
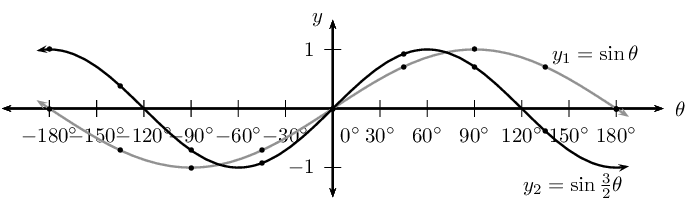
| \(y_1 = \sin \theta\) | \(y_2 = \sin \frac{3\theta}{2}\) | |
| period | \(\text{360}\)\(\text{°}\) | \(\text{240}\)\(\text{°}\) |
| amplitude | \(\text{1}\) | \(\text{1}\) |
| domain | \([-\text{180}\text{°};\text{180}\text{°}]\) | \([-\text{180}\text{°};\text{180}\text{°}]\) |
| range | \([-1;1]\) | \([-1;1]\) |
| maximum turning points | \((\text{90}\text{°};1)\) | \((-\text{180}\text{°};1)\) and \((\text{60}\text{°};1)\) |
| minimum turning points | \((-\text{90}\text{°};-1)\) | \((-\text{60}\text{°};-1) \text{ and } (\text{180}\text{°};1)\) |
| \(y\)-intercept(s) | \((\text{0}\text{°};0)\) | \((\text{0}\text{°};0)\) |
| \(x\)-intercept(s) | \((-\text{180}\text{°};0)\), \((\text{0}\text{°};0)\) and \((\text{180}\text{°};0)\) | \((-\text{120}\text{°};0)\), \((\text{0}\text{°};0)\) and \((\text{120}\text{°};0)\) |
For functions of the general form: \(f(\theta) = y =\sin k\theta\):
Domain and range
The domain is \(\{ \theta: \theta \in \mathbb{R} \}\) because there is no value for \(\theta\) for which \(f(\theta)\) is undefined.
The range is \(\{ f(\theta): -1 \leq f(\theta) \leq 1, f(\theta) \in \mathbb{R} \}\) or \([-1;1]\).
Intercepts
The \(x\)-intercepts are determined by letting \(f(\theta) = 0\) and solving for \(\theta\).
The \(y\)-intercept is calculated by letting \(\theta = \text{0}\text{°}\) and solving for \(f(\theta)\). \begin{align*} y &= \sin k\theta \\ &= \sin \text{0}\text{°} \\ &= 0 \end{align*} This gives the point \((\text{0}\text{°};0)\).
Sketch the following functions for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\) and for each graph determine:
\(f(\theta) =\sin 3\theta\)
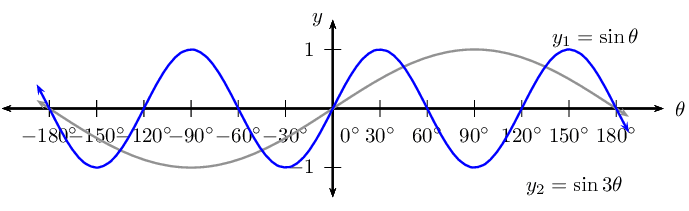
For \(f(\theta) =\sin 3\theta\):
\begin{align*} \text{Period: } & \text{120}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{180}\text{°};0); (-\text{120}\text{°};0); (-\text{60}\text{°};0); \\ & (\text{0}\text{°};0); (\text{60}\text{°};0); (\text{120}\text{°};0); (\text{180}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};0) \\ \text{Max. turning point: } & (-\text{90}\text{°};1); (\text{30}\text{°};1); (\text{150}\text{°};1) \\ \text{Min. turning point: } & (-\text{150}\text{°};-1); (-\text{30}\text{°};-1); (\text{90}\text{°};-1) \end{align*}\(g(\theta) =\sin \frac{\theta}{3}\)
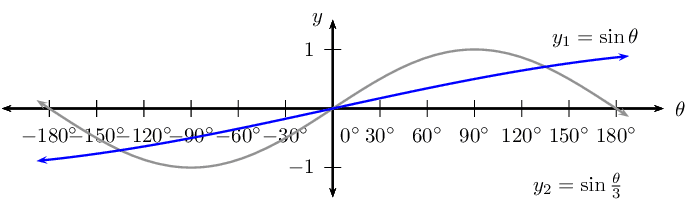
For \(g(\theta) =\sin \frac{\theta}{3}\):
\begin{align*} \text{Period: } & \text{1 080}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-\text{0,87};\text{0,87}] \\ x\text{-intercepts: } & \text{ none } \\ y\text{-intercepts: } & (\text{0}\text{°};0) \\ \text{Max. turning point: } & \text{ none } \\ \text{Min. turning point: } & \text{ none } \end{align*}\(h(\theta) = \sin (-2\theta)\)
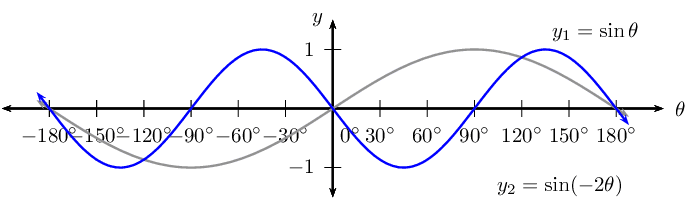
For \(h(\theta) =\sin (-2\theta)\):
\begin{align*} \text{Period: } & \text{180}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{180}\text{°};0); (-\text{90}\text{°};0); (\text{0}\text{°};0); (\text{90}\text{°};0); (\text{180}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};0) \\ \text{Max. turning point: } & (-\text{45}\text{°};1); (\text{135}\text{°};1) \\ \text{Min. turning point: } & (-\text{135}\text{°};-1); (\text{45}\text{°};-1); \end{align*}\(k(\theta) =\sin \frac{3\theta}{4}\)
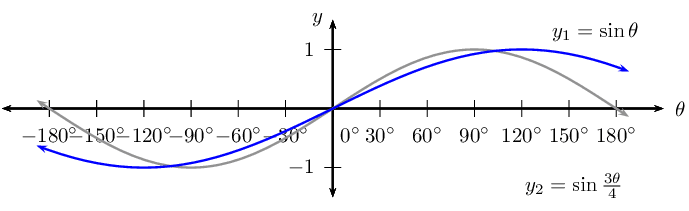
For \(k(\theta) =\sin \frac{3\theta}{4}\):
\begin{align*} \text{Period: } & \text{480}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (\text{0}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};0) \\ \text{Max. turning point: } & (\text{120}\text{°};1) \\ \text{Min. turning point: } & (-\text{120}\text{°};-1); \end{align*}For each graph of the form \(f(\theta) =\sin k\theta\), determine the value of \(k\):
On the same system of axes, plot the following graphs for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\):
Use your sketches of the functions above to complete the following table:
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | \(y_5\) | |
| period | |||||
| amplitude | |||||
| domain | |||||
| range | |||||
| maximum turning points | |||||
| minimum turning points | |||||
| \(y\)-intercept(s) | |||||
| \(x\)-intercept(s) | |||||
| effect of \(p\) |
The effect of the parameter on \(y = \sin(\theta + p)\)
The effect of \(p\) on the sine function is a horizontal shift, also called a phase shift; the entire graph slides to the left or to the right.
For \(p > 0\), the graph of the sine function shifts to the left by \(p\).
For \(p < 0\), the graph of the sine function shifts to the right by \(p\).
|
\(p>0\) |
\(p<0\) |
 |
 |
For each function determine the following:
Notice that for \(y_1 = \sin \theta\) we have \(p = 0\) (no phase shift) and for \(y_2 = \sin (\theta - \text{30}\text{°})\), \(p < 0\) therefore the graph shifts to the right by \(\text{30}\text{°}\).
| θ | \(-\text{360}\)\(\text{°}\) | \(-\text{270}\)\(\text{°}\) | \(-\text{180}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) | \(\text{270}\)\(\text{°}\) | \(\text{360}\)\(\text{°}\) |
| \(\sin \theta\) | \(\text{0}\) | \(\text{1}\) | \(\text{0}\) | \(-\text{1}\) | \(\text{0}\) | \(\text{1}\) | \(\text{0}\) | \(-\text{1}\) | \(\text{0}\) |
| \(\sin(\theta - \text{30}\text{°})\) | \(-\text{0,5}\) | \(\text{0,87}\) | \(\text{0,5}\) | \(-\text{0,87}\) | \(-\text{0,5}\) | \(\text{0,87}\) | \(\text{0,5}\) | \(-\text{0,87}\) | \(-\text{0,5}\) |
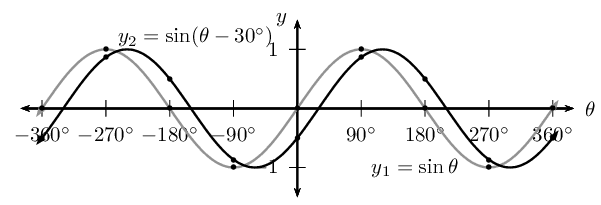
| \(y_1 = \sin \theta\) | \(y_2 = \sin (\theta - \text{30}\text{°})\) | |
| period | \(\text{360}\text{°}\) | \(\text{360}\text{°}\) |
| amplitude | \(\text{1}\) | \(\text{1}\) |
| domain | \([-\text{360}\text{°};\text{360}\text{°}]\) | \([-\text{360}\text{°};\text{360}\text{°}]\) |
| range | \([-1;1]\) | \([-1;1]\) |
| maximum turning points | \((-\text{270}\text{°};1)\) and \((\text{90}\text{°};1)\) | \((-\text{240}\text{°};1)\) and \((\text{120}\text{°};1)\) |
| minimum turning points | \((-\text{90}\text{°};-1)\) and \((\text{270}\text{°};-1)\) | \((-\text{60}\text{°};-1)\) and \((\text{300}\text{°};-1)\) |
| \(y\)-intercept(s) | \((\text{0}\text{°};0)\) | \((\text{0}\text{°};-\frac{1}{2})\) |
| \(x\)-intercept(s) | \((-\text{360}\text{°};0)\), \((-\text{180}\text{°};0)\), \((\text{0}\text{°};0)\), \((\text{180}\text{°};0)\) and \((\text{360}\text{°};0)\) | \((-\text{330}\text{°};0)\), \((-\text{150}\text{°};0)\), \((\text{30}\text{°};0)\) and \((\text{210}\text{°};0)\) |
For functions of the general form: \(f(\theta) = y =\sin (\theta + p)\):
Domain and range
The domain is \(\{ \theta: \theta \in \mathbb{R} \}\) because there is no value for \(\theta\) for which \(f(\theta)\) is undefined.
The range is \(\{ f(\theta): -1 \leq f(\theta) \leq 1, f(\theta) \in \mathbb{R} \}\).
Intercepts
The \(x\)-intercepts are determined by letting \(f(\theta) = 0\) and solving for \(\theta\).
The \(y\)-intercept is calculated by letting \(\theta = \text{0}\text{°}\) and solving for \(f(\theta)\).
Sketch the following functions for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\).
For each function, determine the following:
\(f(\theta) =\sin (\theta + \text{30}\text{°})\)

For \(f(\theta) =\sin (\theta + \text{30}\text{°})\):
\begin{align*} \text{Period: } & \text{360}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{360}\text{°};\text{360}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{210}\text{°};0); (-\text{30}\text{°};0); (\text{150}\text{°};0); (\text{330}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};\frac{1}{2}) \\ \text{Max. turning point: } & (-\text{300}\text{°};1); (\text{60}\text{°};1) \\ \text{Min. turning point: } & (-\text{120}\text{°};-1); (\text{240}\text{°};-1) \end{align*}\(g(\theta) =\sin (\theta - \text{45}\text{°})\)

For \(g(\theta) =\sin (\theta - \text{45}\text{°})\):
\begin{align*} \text{Period: } & \text{360}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{360}\text{°};\text{360}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{315}\text{°};0); (-\text{135}\text{°};0); (\text{45}\text{°};0); (\text{225}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};\frac{1}{\sqrt{2}}) \\ \text{Max. turning point: } & (-\text{300}\text{°};1); (-\text{225}\text{°};1) ; (\text{135}\text{°};1) \\ \text{Min. turning point: } & (-\text{45}\text{°};-1); (\text{315}\text{°};-1) \end{align*}\(h(\theta) =\sin (\theta + \text{60}\text{°})\)

For \(h(\theta) =\sin (\theta + \text{60}\text{°})\):
\begin{align*} \text{Period: } & \text{360}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{360}\text{°};\text{360}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{240}\text{°};0); (-\text{60}\text{°};0); (\text{120}\text{°};0); (\text{300}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};\frac{\sqrt{3}}{2}) \\ \text{Max. turning point: } & (-\text{300}\text{°};1); (-\text{330}\text{°};1) ; (\text{30}\text{°};1) \\ \text{Min. turning point: } & (-\text{150}\text{°};-1); (\text{210}\text{°};-1) \end{align*}Sketch the graph of \(f(\theta) = \sin (\text{45}\text{°} - \theta)\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\).
Write the equation in the form \(y = \sin (\theta + p)\).
\begin{align*} f(\theta) &= \sin (\text{45}\text{°} - \theta)\\ &= \sin (-\theta + \text{45}\text{°}) \\ &= \sin \left( -(\theta - \text{45}\text{°}) \right) \\ &= -\sin (\theta - \text{45}\text{°}) \end{align*}To draw a graph of the above function, we know that the standard sine graph, \(y = \sin\theta\), must:
| θ | \(\text{0}\)\(\text{°}\) | \(\text{45}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{135}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) | \(\text{225}\)\(\text{°}\) | \(\text{270}\)\(\text{°}\) | \(\text{315}\)\(\text{°}\) | \(\text{360}\)\(\text{°}\) |
| \(f(\theta)\) | \(\text{0,71}\) | \(\text{0}\) | \(-\text{0,71}\) | \(-\text{1}\) | \(-\text{0,71}\) | \(\text{0}\) | \(\text{0,71}\) | \(\text{1}\) | \(\text{0,71}\) |
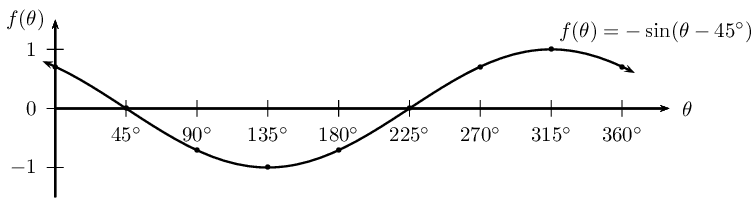
Period: \(\text{360}\text{°}\)
Amplitude: \(\text{1}\)
Domain: \([-\text{360}\text{°};\text{360}\text{°}]\)
Range: \([-1;1]\)
Maximum turning point: \((\text{315}\text{°};1)\)
Minimum turning point: \((\text{135}\text{°};-1)\)
\(y\)-intercepts: \((\text{0}\text{°};\text{0,71})\)
\(x\)-intercept: \((\text{45}\text{°};0) \text{ and } (\text{225}\text{°};0)\)
Sketch the graph of \(f(\theta) = \sin (3\theta + \text{60}\text{°})\) for \(\text{0}\text{°} \leq \theta \leq \text{180}\text{°}\).
Write the equation in the form \(y = \sin k(\theta + p)\).
\begin{align*} f(\theta) &= \sin (3\theta + \text{60}\text{°})\\ &= \sin 3(\theta + \text{20}\text{°}) \end{align*}To draw a graph of the above equation, the standard sine graph, \(y = \sin\theta\), must be changed in the following ways:
| θ | \(\text{0}\)\(\text{°}\) | \(\text{30}\)\(\text{°}\) | \(\text{60}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{120}\)\(\text{°}\) | \(\text{150}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) |
| \(f(\theta)\) | \(\text{0,87}\) | \(\text{0,5}\) | \(-\text{0,87}\) | \(-\text{0,5}\) | \(\text{0,87}\) | \(\text{0,5}\) | \(-\text{0,87}\) |
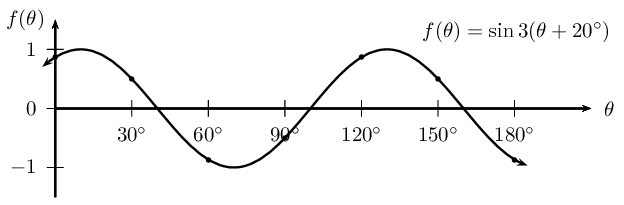
Period: \(\text{120}\text{°}\)
Amplitude: \(\text{1}\)
Domain: \([\text{0}\text{°}; \text{180}\text{°}]\)
Range: \([-1;1]\)
Maximum turning point: \((\text{10}\text{°}; 1) \text{ and } (\text{130}\text{°}; 1)\)
Minimum turning point: \((\text{70}\text{°}; -1)\)
\(y\)-intercept: \((\text{0}\text{°}; \text{0,87})\)
\(x\)-intercepts: \((\text{40}\text{°}; 0)\), \((\text{100}\text{°}; 0)\) and \((\text{160}\text{°}; 0)\)
Sketch the following graphs on separate axes:
\(y = 2 \sin \frac{\theta}{2}\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\)
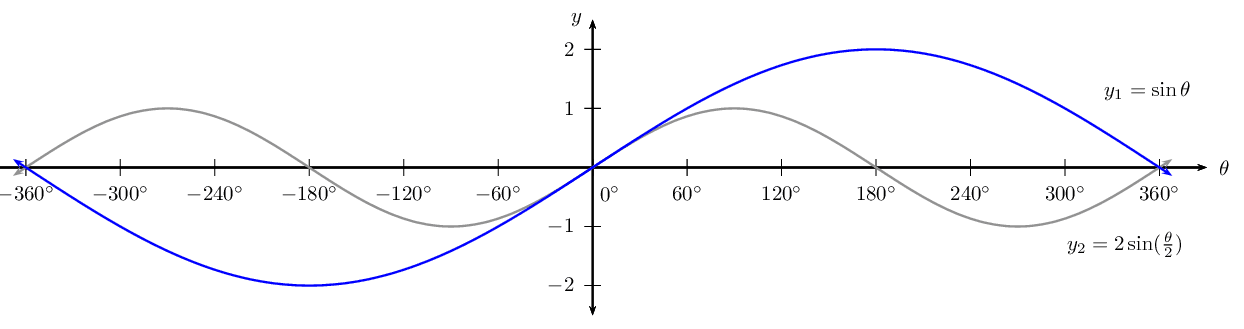
\(f(\theta) = \frac{1}{2} \sin (\theta - \text{45}\text{°})\) for \(-\text{90}\text{°} \leq \theta \leq \text{90}\text{°}\)
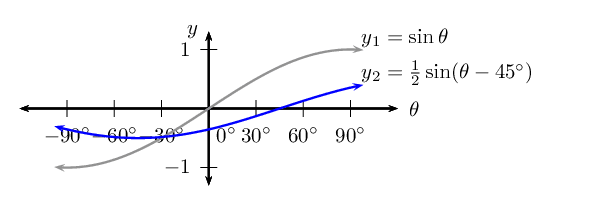
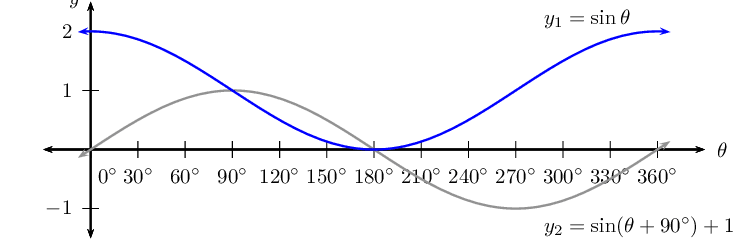
\(y = \sin (\theta + \text{90}\text{°}) + 1\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
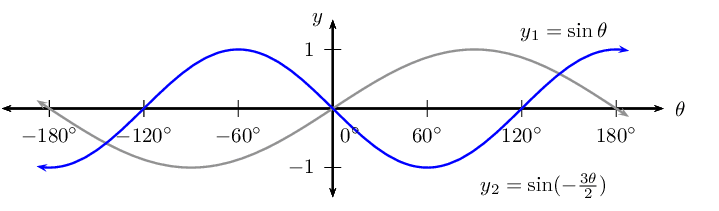
\(y = \sin (-\frac{3\theta}{2})\) for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\)
\(y = \sin (\text{30}\text{°} - \theta)\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\)

Given the graph of the function \(y = a \sin (\theta + p)\), determine the values of \(a\) and \(p\).
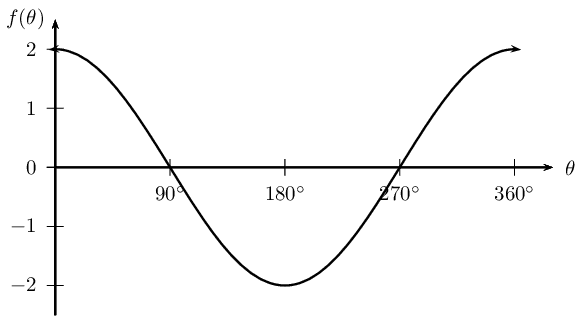
Can you describe this graph in terms of \(\cos \theta\)?
|
Previous
5.4 Exponential functions
|
Table of Contents |
Next
5.6 The cosine function
|