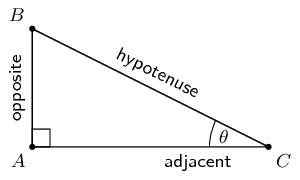
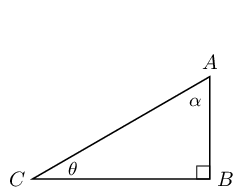
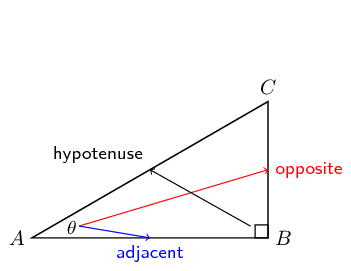
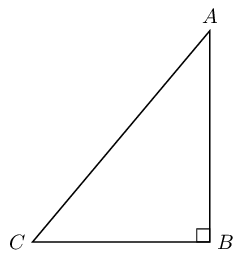
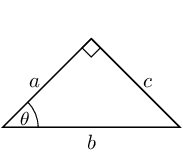
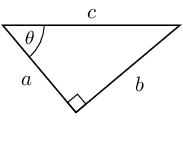
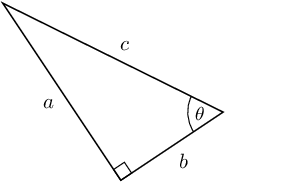
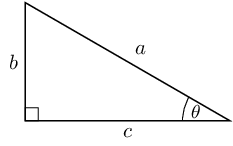
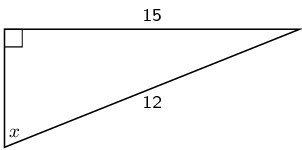
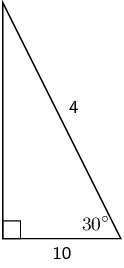
Find \(x\) in the diagram in three different ways. You do not need to
calculate the value of \(x\), just write down the appropriate
ratio for \(x\).
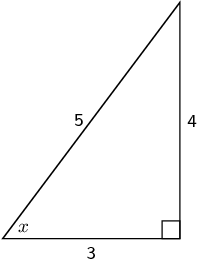
- Side of length 4 is the opposite side
- Side of length 5 is the hypotenuse
- Side of length 3 is the adjacent side
Notice that the hypotenuse is the longest side as we would expect.
\begin{align*}
\sin x & = \frac{4}{5} \\
\cos x & = \frac{3}{5} \\
\tan x & = \frac{4}{3}
\end{align*}
Which of these statements is true about \(\triangle PQR\)?
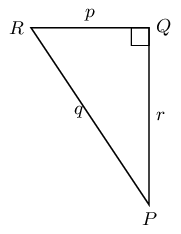
- \(\sin \hat{R} = \dfrac{p}{q}\)
- \(\tan \hat{Q} = \dfrac{r}{p}\)
- \(\cos \hat{P} = \dfrac{r}{q}\)
- \(\sin \hat{P} = \dfrac{p}{r}\)
We first find the opposite and adjacent sides with respect to
\(\hat{P}\) and \(\hat{R}\):
- \(p\) is the opposite side to \(\hat{P}\) and the adjacent
side to \(\hat{R}\)
- \(q\) is the hypotenuse
- \(r\) is the adjacent side to \(\hat{P}\) and the opposite
side to \(\hat{R}\)
We also note that:
- \(\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}\)
- \(\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}\)
- \(\tan \theta = \frac{\text{opposite}}{\text{adjacent}}\)
Looking at each of the given ratios we can see that only \(\cos
\hat{P} = \dfrac{r}{q}\) is correct.
Sarah wants to find the value of \(\alpha\) in the triangle below.
Which statement is a correct line of working?
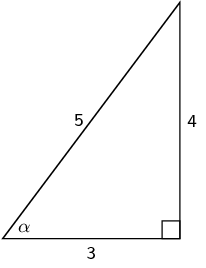
- \(\sin \alpha = \frac{4}{5}\)
- \(\cos \left(\frac{3}{5}\right) = \alpha\)
- \(\tan \alpha = \frac{5}{4}\)
- \(\cos \text{0,8} = \alpha\)
Sarah first needs to identify the hypotenuse, opposite and adjacent
sides in the triangle. She then needs to write down a
trigonometric ratio that will allow her to find \(\alpha\).
\(\sin \alpha = \frac{4}{5}\) is one such ratio that will help her
find \(\alpha\). From the given list of options this is the only
correct line of reasoning.
\(\cos \left(\frac{3}{5}\right) = \alpha\) has the angle and the
lengths of the sides switched around.
\(\tan \alpha = \frac{3}{4}\) uses the wrong sides with respect to
\(\alpha\) for \(\tan\).
\(\cos \text{0,8} = \alpha\) uses the wrong sides with respect to
\(\alpha\) for \(\cos\). Note that you can reduce the fraction
to a decimal number but you need to first write the correct
fraction.