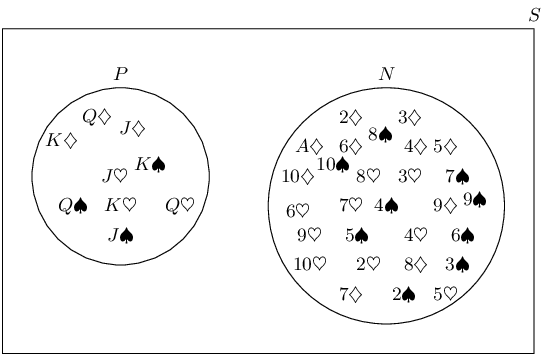
A learner wants to understand the term “outcome”. So the learner rolls a die. Which of the
following is the most appropriate example of the term “outcome”?
We recall the definition of the term “outcome”:
An outcome of an experiment is a single result of that experiment
Therefore the most appropriate example of the term “outcome” is: the die lands on the number 5.
A group of learners are given the following Venn diagram:
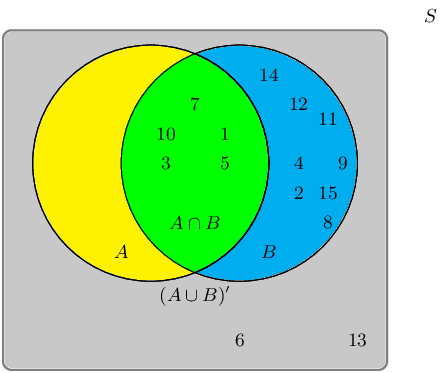
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq
15 \}\).
They are asked to identify the event set of \(B\). They get stuck, and you offer to help them find it.
Which of the following sets best describes the event set of \(B\)?
The event set \(B\) can be shaded as follows:
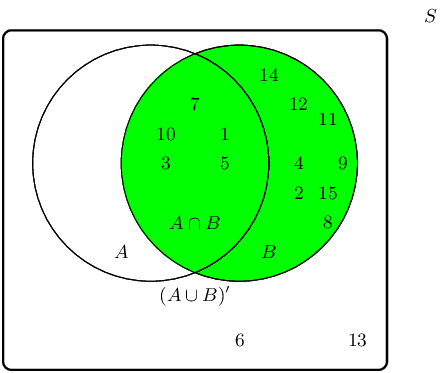
Therefore the event set \(\{1;2;3;4;5;7;8;9;10;11;12;14;15\}\) best describes the event set of \(B\).
A group of learners are given the following Venn diagram:
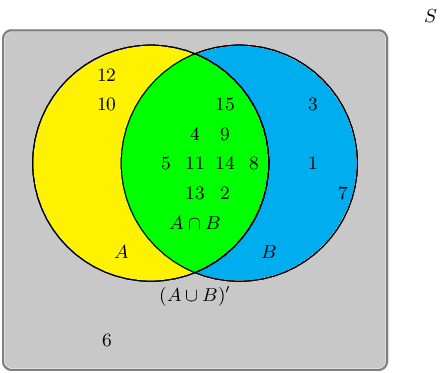
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq
15 \}\).
They are asked to identify the event set of the union between event set \(A\) and event set \(B\), also
written as \(A \cup B\). They get stuck, and you offer to help them find it.
Write down the event set that best describes \(A \cup B\).
The union between event set \(A\) and event set \(B\), also written as \(A \cup B\), can be shaded as
follows:
Therefore the event set \(\{1;2;3;4;5;7;8;9;10;11;12;13;14;15\}\) best describes the event set of \(A \cup
B\).
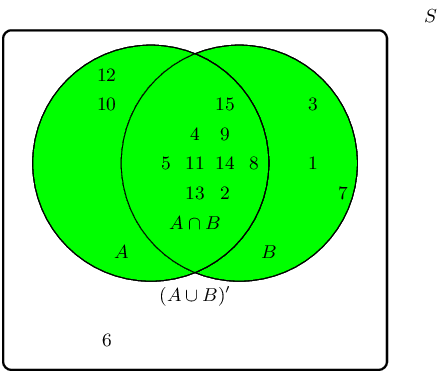
Given the following Venn diagram:
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq
15 \}\).
Are \(A \cup B\) and \((A \cup B)'\) mutually exclusive?
We recall the definition of the term “mutually exclusive”:
Two events are called mutually exclusive if they cannot occur at the same time.
The event set for \(A \cup B\) is: \(\{4;7;8;11;14;15\}\).
The event set for \((A \cup B)'\) is: \(\{1;2;3;5;6;9;10;12;13\}\).
The question we must ask: Can they occur at the same time?
By observing both sets, we can identify the following overlapping event set: \(\{\}\)
Therefore, yes, the event sets \(A \cup B\) and \((A \cup B)'\) are mutually exclusive in this example.
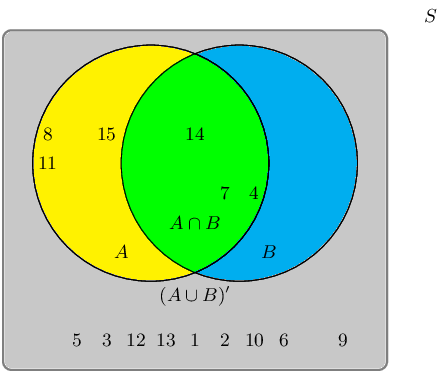
A group of learners are given the following Venn diagram:
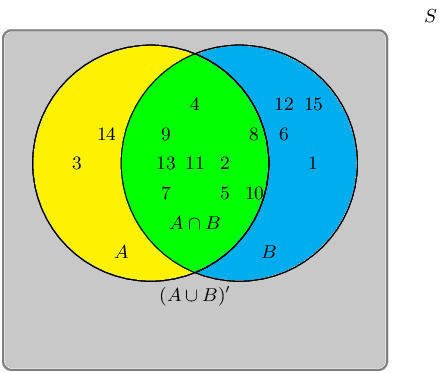
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq
15 \}\).
They are asked to identify the complementary event set of \((A \cap B)\), also known as \((A \cap B)'\).
They get stuck, and you offer to help them find it.
Write down the set that best describes the event set of \((A \cap B)'\).
The event set \((A \cap B)\) can be shaded as follows:
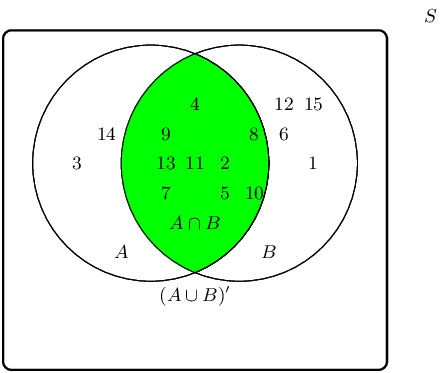
The complementary event set \((A \cap B)'\) can be shaded as follows:
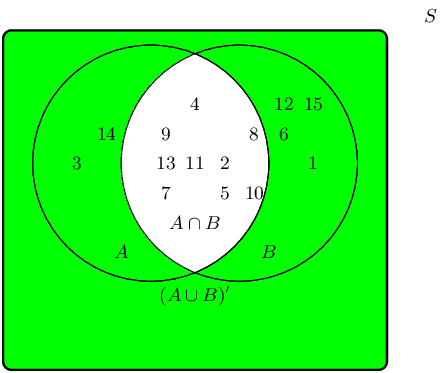
Therefore the event set \(\{1;3;6;12;14;15\}\) best describes the complementary event set of \((A \cap
B)\), also known as \((A \cap B)'\).
A learner finds a deck of 52 cards and then takes one card from the deck. What is the probability that the
card is a king?
Write your answer as a decimal (correct to 2 decimal places).
\begin{align*}
n(E) & = \text{number of outcomes in the event set} = \text{4} \\
n(S) & = \text{number of possible outcomes in the sample space} = \text{52}
\end{align*}
Finally, we calculate the probability:
\begin{align*}
P(E) & = \frac{n(E)}{n(S)} \\
& = \frac{\text{4}}{\text{52}} \\
& \approx \text{0,08}
\end{align*}
Therefore, the probability that the card is a King \(\approx \text{0,08}\).
A die is tossed 21 times and lands 2 times on the number 3.
What is the relative frequency of observing the die land on the number 3? Write your answer correct to 2
decimal places.
Recall the formula:
\[f = \frac{p}{t}\]
Identify variables needed:
\begin{align*}
p & = \text{number of positive trials} = \text{2} \\
f & = \text{total number of trials} = \text{21}
\end{align*}
Calculate the relative frequency:
\begin{align*}
f & = \frac{p}{t} \\
& = \frac{\text{2}}{\text{21}} \\
& = \text{0,10}
\end{align*}
Therefore, the relative frequency of observing the die on the number 3 is \(\text{0,1}\).
A coin is tossed 44 times and lands 22 times on heads.
What is the relative frequency of observing the coin land on heads? Write your answer correct to 2 decimal
places.
Recall the formula:
\[f = \frac{p}{t}\]
Identify variables needed:
\begin{align*}
p & = \text{number of positive trials} = \text{22} \\
f & = \text{total number of trials} = \text{44}
\end{align*}
Calculate the relative frequency:
\begin{align*}
f & = \frac{p}{t} \\
& = \frac{\text{22}}{\text{44}} \\
& = \text{0,50}
\end{align*}
Therefore, the relative frequency of observing the coin on heads is \(\text{0,50}\).
A group of \(\text{45}\) children were asked if they eat Frosties, Strawberry Pops or both. \(\text{31}\)
children said they eat both and \(\text{6}\) said they only eat Frosties. What is the probability that a
child chosen at random will eat only Strawberry Pops?
\begin{align*}
45(\text{all}) - 6(\text{only Frosties}) - 31 (\text{both}) &= 8 (\text{only Strawberry Pops})\\
\therefore \frac{8}{45} &=\text{0,18}
\end{align*}
A packet has yellow sweets and pink sweets. The probability of taking out a pink sweet is \(\frac{7}{12}\).
What is the probability of taking out a yellow sweet?
\(1 - \frac{7}{12} = \frac{5}{12}\)
the sum of the numbers is \(\text{4}\).
\(S = \{(1,1);(1,2);(2,1);(2,2);(3,1);(3,2)\}\)
\begin{align*}
P &= \frac{n(E)}{n(S)} \\
P &= \frac{2}{6} \\
\therefore P &= \frac{1}{3}
\end{align*}
the sum of the two numbers is a prime number.
\begin{align*}
P &= \frac{n(E)}{n(S)} \\
P &= \frac{4}{6} \\
\therefore P &= \frac{2}{3}
\end{align*}
the product of the two numbers is at least \(\text{3}\).
\begin{align*}
P &= \frac{n(E)}{n(S)} \\
P &= \frac{3}{6} \\
\therefore P &= \frac{1}{2}
\end{align*}
the sum is equal to the product.
\begin{align*}
P &= \frac{n(E)}{n(S)} \\
P &= \frac{1}{6}
\end{align*}
A group of learners is given the following event sets:
\[\begin{array}{|l|c|c|}
\hline
\text{Event Set } A & 3 & 4 \\
\hline
\end{array}\]
\[\begin{array}{|l|c|c|c|}
\hline
\text{Event Set } B & 2 & 4 & 5 \\
\hline
\end{array}\]
\[\begin{array}{|l|c|c|c|c|}
\hline
\text{Event Set } A \cup B & 2 & 3 & 4 & 5 \\
\hline
\end{array}\]
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq
6 \}\)
They are asked to calculate the value of \(P(A \cap B)\). They get stuck, and you offer to calculate it for
them. Give your answer as a decimal number, rounded to two decimal value.
\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]
Make \(P(A \cap B)\) the subject, and we get:
\begin{align*}
P (A \cap B) & = P(B) + P(A) - P(A \cup B)
\end{align*}
Identify variables needed:
\begin{align*}
P(A) & = \frac{n(A)}{n(S)} = \frac{2}{6} = \text{0,33} \\
P(B) & = \frac{n(B)}{n(S)} = \frac{3}{6} = \text{0,5} \\
P(A \cup B) & = \frac{n(A \cup B)}{n(S)} = \frac{4}{6} = \text{0,67}
\end{align*}
Calculate \(P(A \cap B)\):
\begin{align*}
P (A \cap B) & = P(B) + P(A) - P(A \cup B) \\
& = (\text{0,5}) + (\text{0,33}) - (\text{0,67}) \\
& = \text{0,17}
\end{align*}
Therefore, the value of \(P(A \cap B)\) is \(\text{0,17}\).
Use a Venn diagram to prove that the probability of either event A or B occurring (A and B are not mutually
exclusive) is given by:
\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]
|
\(P\left(A\right)\)
|
\(+\)
|
|
\(P\left(B\right)\)
|
\(-\)
|
\(P\left(A\cap B\right)\)
|
|
|
\(=\)
|

|
\(+\)
|
\(\big(\)
|

|
\(-\)
|

|
\(\big)\)
|
|
\(=\)
|

|
\(+\)
|
|

|
|
|
|
|
\(=\)
|

|
|
|
|
|
|
|
|
\(=\)
|
\(P\left(A\cup B\right)\)
|
|
|
|
|
|
|
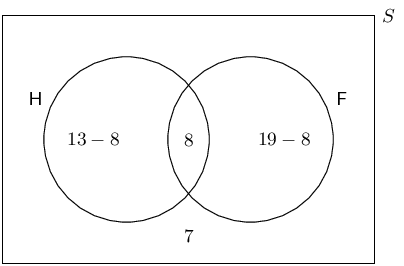
In a class there are
-
8 learners who play football and hockey
-
7 learners who do not play football or hockey
-
13 learners who play hockey
-
19 learners who play football
How many learners are there in the class?
Let \(H\) and \(F\) be the learners who play hockey and football respectively.