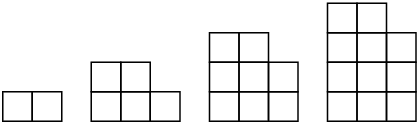
\(4 \; ; \; 13 \; ; \; 22 \; ; \; 31 \; ; \; \ldots\)
We first need to find \(d\):
\begin{align*}
d & = T_{2} - T_{1} \\
& = 13 - 4 \\
& = 9
\end{align*}
Next we note that for each successive term we add \(d\) to the last term. We can express this as:
\begin{align*}
T_{1} & = a = 4 \\
T_{2} & = a + d = 4 + 9 \\
& = 4 + 9(1)\\
T_{3} & = T_{2} + d = 4 + 9 + 9 \\
& = 4 + 9(2) \\
T_{n} & = T_{n-1} + d = 4 + 9(n-1) \\
& = 9n - 5
\end{align*}
The general formula is \(T_n = 9n - 5\).
\(T_{6}\) is:
\begin{align*}
T_{6} & = 9(6) - 5 \\
& = 49
\end{align*}
\(T_{6} = \text{49}\)
\(5 \; ; \; 2 \; ; \; -1 \; ; \; -4 \; ; \; \ldots\)
We first need to find \(d\):
\begin{align*}
d & = T_{2} - T_{1} \\
& = 2 - 5 \\
& = -3
\end{align*}
Next we note that for each successive term we add \(d\) to the last term. We can express this as:
\begin{align*}
T_{1} & = a = 5 \\
T_{2} & = a + d = 5 + (-3) \\
& = 5 + (-3)(1)\\
T_{3} & = T_{2} + d = 5 + (-3) + (-3) \\
& = 5 + (-3)(2) \\
T_{n} & = T_{n-1} + d = 5 + (-3)(n-1) \\
& = 7 - 3n
\end{align*}
The general formula is \(T_n = 7 - 3n\).
\(T_{6}\) is:
\begin{align*}
T_{6} & = 7 - 3(6) \\
& = -11
\end{align*}
\(T_{6} = -\text{11}\)
\(\text{7,4} \; ; \; \text{9,7} \; ; \; \text{12} \; ; \; \text{14,3} \; ; \; \ldots\)
We first need to find \(d\):
\begin{align*}
d & = T_{2} - T_{1} \\
& = \text{9,7} - \text{7,4} \\
& = \text{2,3}
\end{align*}
Next we note that for each successive term we add \(d\) to the last term. We can express this as:
\begin{align*}
T_{1} & = a = \text{7,4} \\
T_{2} & = a + d = \text{7,4} + \text{2,3} \\
& = \text{7,4} + \text{2,3}(1)\\
T_{3} & = T_{2} + d = \text{7,4} + \text{2,3} + \text{2,3} \\
& = \text{7,4} + \text{2,3}(2) \\
T_{n} & = T_{n-1} + d = \text{7,4} + \text{2,3}(n-1) \\
& = \text{7,4} + \text{2,3}n - \text{2,3} = \text{2,3}n + \text{5,1}
\end{align*}
The general formula is \(T_n = \text{2,3}n + \text{5,1}\).
\(T_{6}\) is:
\begin{align*}
T_{6} & = \text{2,3}(6) + \text{5,1} \\
& = \text{18,9}
\end{align*}
\(T_{6} = \text{18,9}\)