13.4 The effect of multiplying a dimension by a factor of k

13.3 Right pyramids, right cones and spheres

13.4 The effect of multiplying a dimension by a factor of k (EMA7T)

When one or more of the dimensions of a prism or cylinder is multiplied by a constant, the surface area and volume will change. The new surface area and volume can be calculated by using the formulae from the preceding section.

It is possible to see a relationship between the change in dimensions and the resulting change in surface area and volume. These relationships make it simpler to calculate the new volume or surface area of an object when its dimensions are scaled up or down.

Consider a rectangular prism of dimensions $l$, $b$ and $h$. Below we multiply one, two and three of its dimensions by a constant factor of $\text{5}$ and calculate the new volume and surface area.

Dimensions	Volume	Surface
Original dimensions	$\begin{array}{rl} V& =l\times b\times h\\ & =lbh \end{array}$	$\begin{array}{rl} A& =2\left[\left(l\times h\right)+\left(l\times b\right)+\left(b\times h\right)\right]\\ & =2\left(lh+lb+bh\right) \end{array}$
Multiply one dimension by $\text{5}$	$\begin{array}{rl} {V}_{1}& =l\times b\times 5h\\ & =5\left(lbh\right)\\ & =5V \end{array}$	$\begin{array}{rl} {A}_{1}& =2\left[\left(l\times 5h\right)+\left(l\times b\right)+\left(b\times 5h\right)\right]\\ & =2\left(5lh+lb+5bh\right) \end{array}$
Multiply two dimensions by $\text{5}$	$\begin{array}{rl} {V}_{2}& =5l\times b\times 5h\\ & =5.5\left(lbh\right)\\ & ={5}^{2}\times V \end{array}$	$\begin{array}{rl} {A}_{2}& =2\left[\left(5l\times 5h\right)+\left(5l\times b\right)+\left(b\times 5h\right)\right]\\ & =2\times 5\left(5lh+lb+bh\right) \end{array}$
Multiply all three dimensions by $\text{5}$	$\begin{array}{rl} {V}_{3}& =5l\times 5b\times 5h\\ & ={5}^{3}\left(lbh\right)\\ & ={5}^{3}V \end{array}$	$\begin{array}{rl} {A}_{3}& =2\left[\left(5l\times 5h\right)+\left(5l\times 5b\right)+\left(5b\times 5h\right)\right]\\ & =2\left({5}^{2}lh+{5}^{2}lb+{5}^{2}bh\right)\\ & ={5}^{2}\times 2\left(lh+lb+bh\right)\\ & ={5}^{2}A \end{array}$
Multiply all three dimensions by k	$\begin{array}{rl} {V}_{k}& =kl\times kb\times kh\\ & ={k}^{3}\left(lbh\right)\\ & ={k}^{3}V \end{array}$	$\begin{array}{rl} {A}_{k}& =2\left[\left(kl\times kh\right)+\left(kl\times kb\right)+\left(kb\times kh\right)\right]\\ & ={k}^{2}\times 2\left(lh+lb+bh\right)\\ & ={k}^{2}A \end{array}$

Worked example 18: Calculating the new dimensions of a rectangular prism

Consider a rectangular prism with a height of $\text{4}$ $\text{cm}$ and base lengths of $\text{3}$ $\text{cm}$.

Calculate the surface area and volume.
Calculate the new surface area (${A}_{n}$) and volume (${V}_{n}$) if the base lengths are multiplied by a constant factor of $\text{3}$.
Express the new surface area and volume as a factor of the original surface area and volume.

Calculate the original volume and surface area

\begin{align*} V & =l\times b\times h \\ & = 3 \times 3 \times 4 \\ & = \text{36}\text{ cm$^{3}$} \\ \\ A& = 2\left[\left(l\times h\right) + \left(l\times b\right) + \left(b\times h\right)\right] \\ & = 2\left[\left(3\times 4\right) + \left(3\times 3\right) + \left(3\times 4\right)\right] \\ & = \text{66}\text{ cm$^{2}$} \end{align*}

Calculate the new volume and surface area

Two of the dimensions are multiplied by a factor of 3.

\begin{align*} {V}_{n} & = 3l \times 3b\times h \\ & = 3(3) \times 3(3) \times 4 \\ & = \text{324}\text{ cm$^{3}$} \\ \\ {A}_{n} & = 2\left[\left(3l \times h\right) + \left(3l \times 3b \right) + \left(3b\times h\right)\right] \\ & = 2\left[\left(3(3) \times 4\right) + \left(3(3) \times 3(3)\right) + \left(3(3)\times 4\right)\right] \\ & = \text{306}\text{ cm$^{2}$} \end{align*}

Express the new dimensions as a factor of the original dimensions

\begin{align*} V & = 36 \\ {V}_{n} & = 324 \\ \frac{{V}_{n}}{V} & = \frac{324}{36} \\ & = 9 \\ \therefore {V}_{n} & = 9V \\ & = {3}^{2}V \\ \\ A& = 66 \\ {A}_{n} & = 306 \\ \frac{{A}_{n}}{A} & = \frac{306}{66} \\ \therefore {A}_{n}& = \frac{306}{66}A \\ & = \frac{51}{11}A \end{align*}

Worked example 19: Multiplying the dimensions of a rectangular prism by $k$

Prove that if the height of a rectangular prism with dimensions $l$, $b$ and $h$ is multiplied by a constant value of $k$, the volume will also increase by a factor $k$.

Calculate the original volume

We are given the original dimensions $l$, $b$ and $h$ and so the original volume is $V = l \times b \times h$.

Calculate the new volume

The new dimensions are $l$, $b$, and $kh$ and so the new volume is:

\begin{align*} {V}_{n} & = l \times b \times \left(kh\right) \\ & = k \left(lbh\right) \\ & = kV \end{align*}

Write the final answer

If the height of a rectangular prism is multiplied by a constant $k$, then the volume also increases by a factor of $k$.

Worked example 20: Multiplying the dimensions of a cylinder by $k$

Consider a cylinder with a radius of $r$ and a height of $h$. Calculate the new volume and surface area (expressed in terms of $r$ and $h$) if the radius is multiplied by a constant factor of $k$.

Calculate the original volume and surface area

\begin{align*} V & = \pi {r}^{2} \times h \\ A & = \pi {r}^{2} + 2 \pi rh \end{align*}

Calculate the new volume and surface area

The new dimensions are $kr$ and $h$.

\begin{align*} {V}_{n} & =\pi {\left(kr\right)}^{2}\times h \\ & = \pi {k}^{2}{r}^{2}\times h \\ & = {k}^{2}\times \pi {r}^{2}h \\ & = {k}^{2}V \\ \\ {A}_{n} & = \pi {\left(kr\right)}^{2} + 2\pi \left(kr\right)h \\ & = \pi {k}^{2}{r}^{2} + 2\pi krh \\ & = {k}^{2}\left(\pi {r}^{2}\right) + k\left(2\pi rh\right) \end{align*}

Textbook Exercise 13.6

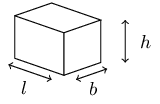
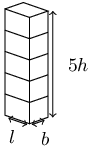
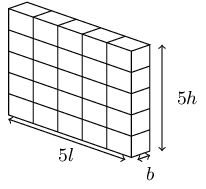
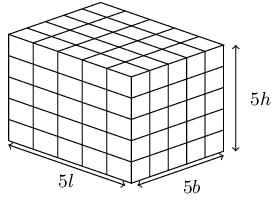
If the length of the radius of a circle is a third of its original size, what will the area of the new circle be?

The area of the original circle is: $\pi r^{2}$. Now we reduce the radius by a third. In other words we multiply $r$ by one third. The new area is:

\begin{align*} A_{\text{new}} & = \pi \left(\frac{1}{3}r\right)^{2} \\ & = \frac{1}{9} \pi r^{2} \\ & = \frac{1}{9} A \end{align*}

Therefore, if the radius of a circle is a third of its original size, the area of the new circle will be $\frac{1}{9}$ the original area.

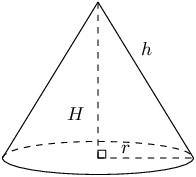
If the length of the base's radius and height of a cone is doubled, what will the surface area of the new cone be?

We can find the new area by noting that the area will change by a factor of $k$ when we change the dimensions of the cone. In this case we are changing two dimensions of the cone and so the new area will be: $A_{\text{new}} = k^{2}A$

The value of $k$ comes from the word “doubled” in the question: the value of $k$ is 2.

So the new area of the cone will be $A_{\text{new}} = 4 \times A$ if we double the height and the base's radius of the cone.

Therefore the surface area of the new cone will be 4 times the original surface area.

If the height of a prism is doubled, how much will its volume increase by?

We do not know if we have a rectangular prism or a triangular prism. However we do know that the volume of a prism is given by:

\[V = \text{area of base} \times \text{height of prism}\]

Now we are changing just one dimension of the prism: the height. Therefore the new volume is given by:

\begin{align*} V_{\text{new}} & = \text{area of base} \times 2(\text{height of prism}) \\ & = 2V \end{align*}

Therefore the volume of the prism doubles if the height is doubled.

length and breadth increase by a constant factor of $\text{3}$.

The volume of a rectangular prism is given by $V = l \times b \times h$. If we increase the length and breadth by a constant factor of 3 the volume is:

\begin{align*} V_{\text{new}} & = 3(l) \times 3(b) \times h \\ & = 9 V \end{align*}

Therefore the volume of the prism increases by a factor of 9 when the length and breadth are increased by a constant factor of 3.

length, breadth and height are multiplied by a constant factor of $\text{3}$.

The volume of a rectangular prism is given by $V = l \times b \times h$. If we increase the length, breadth and height by a constant factor of 3 the volume is:

\begin{align*} V_{\text{new}} & = 3(l) \times 3(b) \times 3(h) \\ & = 27 V \end{align*}

Therefore the volume of the prism increases by a factor of 27 when the length, breadth and height are increased by a constant factor of 3.

If the length of each side of a triangular prism is quadrupled, what will the volume of the new triangular prism be?

When multiplied by a factor of $k$ the volume of a shape will increase by $k^{3}$. We are told that the dimensions are quadrupled. This means that each dimension is multiplied by 4. Therefore $k = 4$.

Now we can calculate $k^{3}$.

\[k^{3} = \left( 4 \right)^3 = 64\]

Therefore, if each side of a triangular prism is quadrupled, the volume of the new triangular prism will be 64 times the original shape's volume.

Given a prism with a volume of $\text{493}$ $\text{cm$^{3}$}$ and a surface area of $\text{6 007}$ $\text{cm$^{2}$}$, find the new surface area and volume for a prism if all dimensions are increased by a constant factor of $\text{4}$.

We are increasing all the dimensions by 4 and so the volume will increase by $4^{3}$. The surface area will increase by $4^{2}$.

\begin{align*} V &= 493 \times 4^{3} \\ & = \text{31 552}\text{ cm$^{3}$} \\ \text{Surface area} &= \text{6 007} \times 4^{2} \\ &= \text{96 112}\text{ cm$^{2}$} \end{align*}

Therefore the volume is $\text{31 552}$ $\text{cm$^{3}$}$ and the surface area is $\text{96 112}$ $\text{cm$^{2}$}$.

13.3 Right pyramids, right cones and spheres

Table of Contents

13.5 Chapter summary

Dimensions	Volume	Surface
Original dimensions	\(\begin{array}{rl} V& =l\times b\times h\\ & =lbh \end{array}\)	\(\begin{array}{rl} A& =2\left[\left(l\times h\right)+\left(l\times b\right)+\left(b\times h\right)\right]\\ & =2\left(lh+lb+bh\right) \end{array}\)
Multiply one dimension by \(\text{5}\)	\(\begin{array}{rl} {V}_{1}& =l\times b\times 5h\\ & =5\left(lbh\right)\\ & =5V \end{array}\)	\(\begin{array}{rl} {A}_{1}& =2\left[\left(l\times 5h\right)+\left(l\times b\right)+\left(b\times 5h\right)\right]\\ & =2\left(5lh+lb+5bh\right) \end{array}\)
Multiply two dimensions by \(\text{5}\)	\(\begin{array}{rl} {V}_{2}& =5l\times b\times 5h\\ & =5.5\left(lbh\right)\\ & ={5}^{2}\times V \end{array}\)	\(\begin{array}{rl} {A}_{2}& =2\left[\left(5l\times 5h\right)+\left(5l\times b\right)+\left(b\times 5h\right)\right]\\ & =2\times 5\left(5lh+lb+bh\right) \end{array}\)
Multiply all three dimensions by \(\text{5}\)	\(\begin{array}{rl} {V}_{3}& =5l\times 5b\times 5h\\ & ={5}^{3}\left(lbh\right)\\ & ={5}^{3}V \end{array}\)	\(\begin{array}{rl} {A}_{3}& =2\left[\left(5l\times 5h\right)+\left(5l\times 5b\right)+\left(5b\times 5h\right)\right]\\ & =2\left({5}^{2}lh+{5}^{2}lb+{5}^{2}bh\right)\\ & ={5}^{2}\times 2\left(lh+lb+bh\right)\\ & ={5}^{2}A \end{array}\)
Multiply all three dimensions by k	\(\begin{array}{rl} {V}_{k}& =kl\times kb\times kh\\ & ={k}^{3}\left(lbh\right)\\ & ={k}^{3}V \end{array}\)	\(\begin{array}{rl} {A}_{k}& =2\left[\left(kl\times kh\right)+\left(kl\times kb\right)+\left(kb\times kh\right)\right]\\ & ={k}^{2}\times 2\left(lh+lb+bh\right)\\ & ={k}^{2}A \end{array}\)