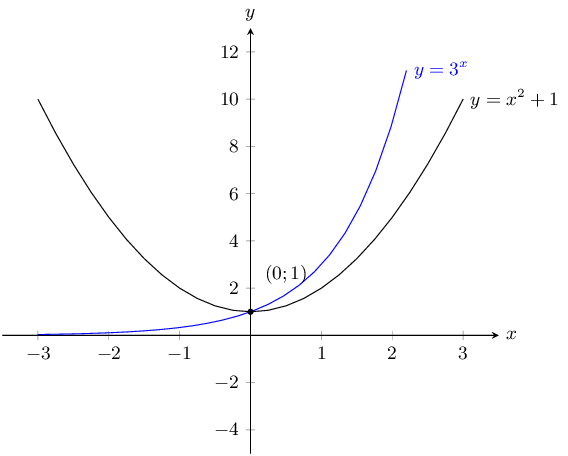
\(y = x^2 +1\) and \(y = 3^x\)
The \(y\)-intercept for each graph is:
\(\begin{aligned} 0^2 + 1 & = 1 \\ 3^0 & = 1 \end{aligned}\)This is also the only point of intersection.
For both graphs there is no \(x\)-intercept.
|
Previous
6.6 Trigonometric functions
|
Next
6.8 Chapter summary
|
Use the sketch below to determine the values of \(a\) and \(q\) for the parabola of the form \(y=a{x}^{2}+q\).
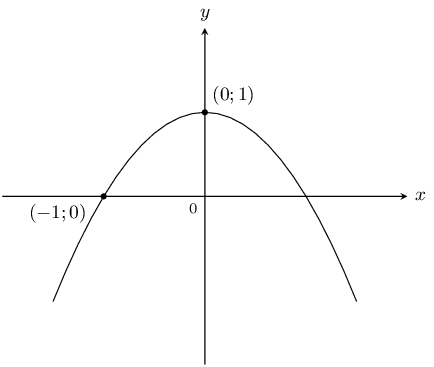
From the sketch we see that the shape of the graph is a “frown”, therefore \(a<0\). We also see that the graph has been shifted vertically upwards, therefore \(q>0\).
The \(y\)-intercept is the point \((0;1)\).
\begin{align*} y& = a{x}^{2}+q \\ 1& = a{(0)}^{2}+q \\ \therefore q& = 1 \end{align*}Substitute point \((-1;0)\) into the equation:
\begin{align*} y& = a{x}^{2}+q \\ 0& = a{(-1)}^{2}+1 \\ \therefore a& = -1 \end{align*}\(a=-1\) and \(q=1\), so the equation of the parabola is \(y=-{x}^{2}+1\).
Use the sketch below to determine the values of \(a\) and \(q\) for the hyperbola of the form \(y=\frac{a}{x}+q\).
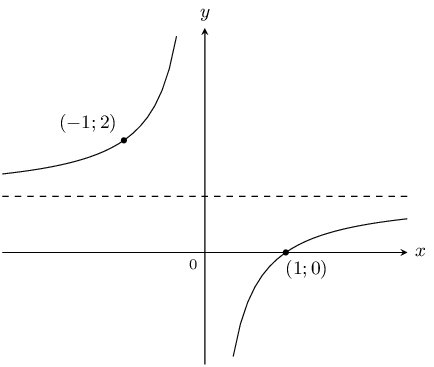
The two curves of the hyperbola lie in the second and fourth quadrant, therefore \(a<0\). We also see that the graph has been shifted vertically upwards, therefore \(q>0\).
Substitute the point \((-1;2)\):
\begin{align*} y& = \frac{a}{x}+q \\ 2& = \frac{a}{-1}+q \\ \therefore 2& = -a+q \end{align*}Substitute the point \((1;0)\):
\begin{align*} y& = \frac{a}{x}+q \\ 0& = \frac{a}{1}+q \\ \therefore a& = -q \end{align*}\(a=-1\) and \(q=1\), therefore the equation of the hyperbola is \(y=\dfrac{-1}{x}+1\).
The graphs of \(y=-{x}^{2}+4\) and \(y=x-2\) are given. Calculate the following:
coordinates of \(A\), \(B\), \(C\), \(D\)
coordinates of \(E\)
distance \(CD\)
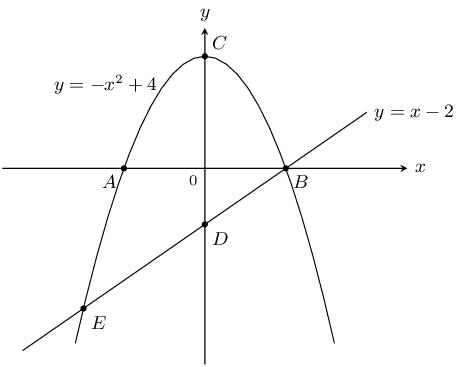
For the parabola, to calculate the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = -{x}^{2}+4 \\ & = -{0}^{2}+4 \\ & = 4 \end{align*}This gives the point \(C(0;4)\).
To calculate the \(x\)-intercept, let \(y=0\):
\begin{align*} y& = -{x}^{2}+4 \\ 0& = -{x}^{2}+4 \\ {x}^{2}-4& = 0 \\ (x+2)(x-2)& = 0 \\ \therefore x& = ±2 \end{align*}This gives the points \(A(-2;0)\) and \(B(2;0)\).
For the straight line, to calculate the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = x-2 \\ & = 0-2 \\ & = -2 \end{align*}This gives the point \(D(0;-2)\).
At \(E\) the two graphs intersect so we can equate the two expressions:
\begin{align*} x-2& = -{x}^{2}+4 \\ \therefore {x}^{2}+x-6& = 0 \\ \therefore (x-2)(x+3)& = 0 \\ \therefore x& = 2 \text{ or } -3 \end{align*}At \(E\), \(x=-3\), therefore \(y=x-2=-3-2=-5\). This gives the point \(E(-3;-5)\).
Distance \(CD\) is \(\text{6}\) units.
coordinates of \(A(-2;0)\), \(B(2;0)\), \(C(0;4)\), \(D(0;-2)\)
coordinates of \(E(-3;-5)\)
distance \(CD = 6\) units
Use the sketch to determine the equation of the trigonometric function \(f\) of the form \(y=a f(\theta)+q\).
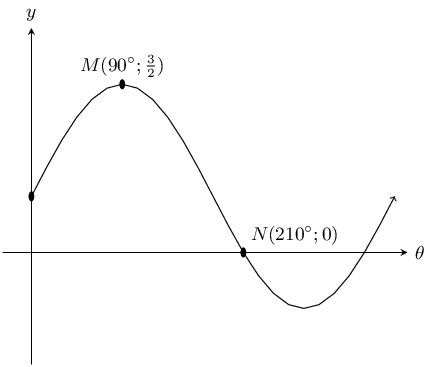
From the sketch we see that the graph is a sine graph that has been shifted vertically upwards. The general form of the equation is \(y=a\sin\theta +q\).
At \(N\), \(\theta =210°\) and \(y=0\):
\begin{align*} y& = a\sin\theta +q \\ 0& = a\sin 210°+q \\ & = a\left(-\frac{1}{2}\right)+q \\ \therefore q& = \frac{a}{2} \end{align*}At \(M\), \(\theta = 90°\) and \(y=\frac{3}{2}\):
\begin{align*} \frac{3}{2}& = a\sin90°+q \\ & = a+q \end{align*}Plot the following functions on the same set of axes and clearly label all the points at which the functions intersect.
\(y = x^2 +1\) and \(y = 3^x\)
The \(y\)-intercept for each graph is:
\(\begin{aligned} 0^2 + 1 & = 1 \\ 3^0 & = 1 \end{aligned}\)This is also the only point of intersection.
For both graphs there is no \(x\)-intercept.

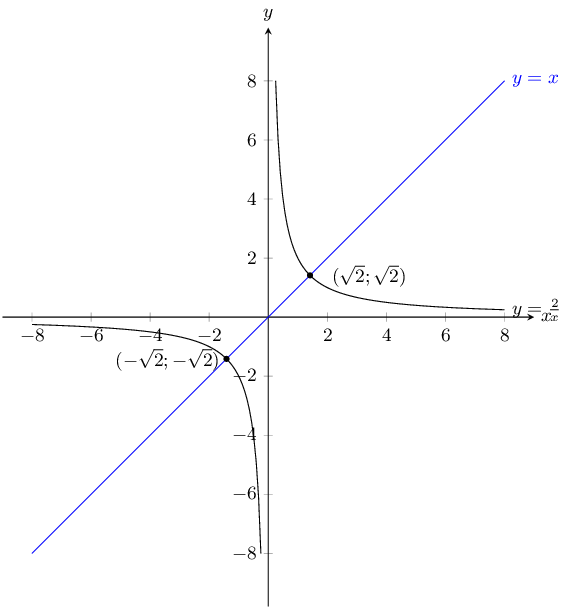
\(y = x\) and \(y = \dfrac{2}{x}\)
\(y = x\) is a basic straight line graph. For \(y =\frac{2}{x}\) there is no \(y\)-intercept and no \(x\)-intercept. We note that this is a hyperbolic graph that has been stretched by 2 units.
The points of intersection are:
\begin{align*} x &= \frac{2}{x} \\ x^2 &= 2 \\ x^2 - 2 & = 0\\ (x - \sqrt{2})(x + \sqrt{2}) & = 0\\ x = \sqrt{2} &\text{ or } x = -\sqrt{2} \\ y = \sqrt{2} &\text{ or } y = -\sqrt{2} \end{align*}The graphs intersect at \(\left(\sqrt{2};\sqrt{2}\right)\) and \(\left(-\sqrt{2};-\sqrt{2}\right)\).
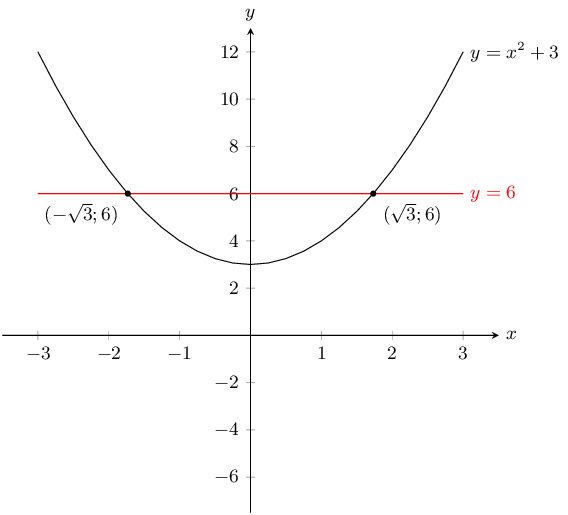
\(y = x^2 +3\) and \(y = 6\)
\(y = 6\) is a horizontal line through \((0;6)\). For \(y =x^2 + 3\) the \(y\)-intercept is \((0;3)\) and there are no \(x\)-intercepts. From the value of \(q\) we see that this is a basic parabola that has been shifted upwards by 3 units.
The points of intersection are:
\begin{align*} x^2 + 3 &= 6 \\ x^2 - 3 &= 0 \\ (x - \sqrt{3})(x + \sqrt{3}) & = 0\\ x = \sqrt{3} &\text{ or } x = -\sqrt{3} \\ y = 6 \end{align*}The graphs intersect at \(\left(\sqrt{3};6\right)\) and \(\left(-\sqrt{3};-6\right)\).
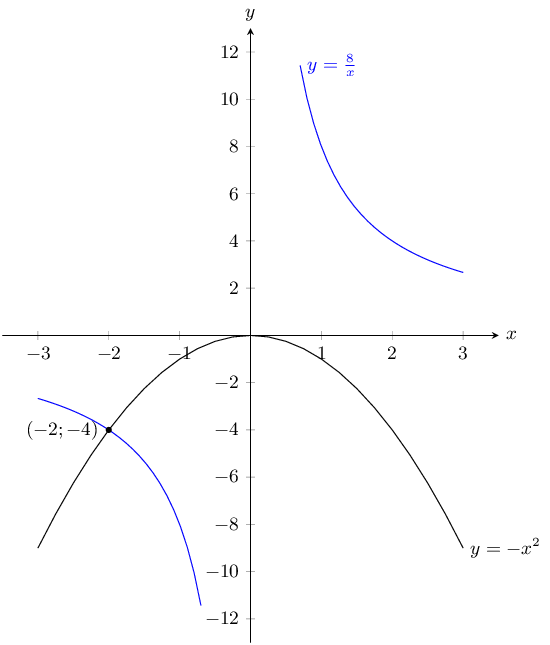
\(y = -x^2\) and \(y = \dfrac{8}{x}\)
\(y = -x^{2}\) is a parabola that has been reflected about the \(x\)-axis. For \(y =\frac{8}{x}\) there is no \(y\)-intercept and there is no \(x\)-intercepts. From the value of \(a\) we see that this is a basic hyperbola that has been stretched by 8 units.
The points of intersection are:
\begin{align*} -x^2 &= \frac{8}{x} \\ x^3 &= - 8 \\ x & = -2\\ y &= \frac{8}{-2} \\ y &= -4 \end{align*}The graphs intersect at \(\left(-2;-4\right)\).
Determine the equations for the graphs given below.

For the straight line graph we have the \(x\) and \(y\)-intercepts. The \(y\)-intercept gives \(c = 2\). Now we can calculate the gradient of the straight line graph:
\begin{align*} y &= mx + 2 \\ m &= \frac{2 - 0}{0 - (-2)} \\ &= 1 \end{align*}Therefore the equation of the straight line graph is \(y = x + 2\).
For the parabola we also have the \(x\) and \(y\)-intercepts. The \(y\)-intercept gives \(q = 2\). Now we can calculate \(a\):
\begin{align*} y &= ax^2 + 2 \\ 0 &= a(-2)^2 + 2 \\ -2 &= 4a \\ a &= -\frac{1}{2} \end{align*}Therefore the equation of the parabola is \(y = -\frac{1}{2}x^2 + 2\).
The equations for the two graphs are \(y = x + 2\) and \(y = -\frac{1}{2}x^2 + 2\)
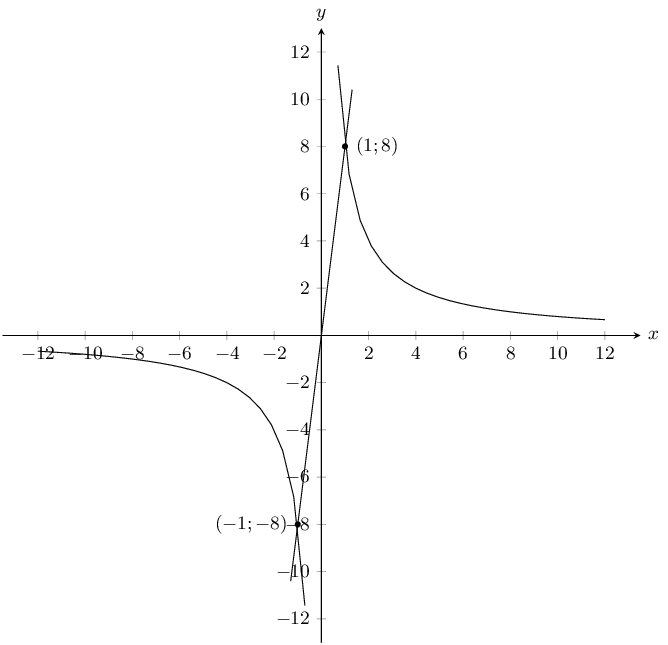
For the straight line graph we notice that it passes through \((0;0)\) and so \(c = 0\).
We have two points on the straight line graph and so we can calculate the gradient, \(m\):
\begin{align*} y &= mx + 0 \\ m &= \frac{8 - (-8)}{1 - (- 1)} \\ m &= 8 \end{align*}The equation of the straight line graph is \(y = 8x\).
For the hyperbola we note that the graph is not shifted either upwards or downwards. Therefore \(q = 0\). Now we can calculate \(a\):
\begin{align*} y &= \frac{a}{x} \\ 8 &= \frac{a}{1} \\ a &= 8 \end{align*}Therefore the equation of the hyperbola is \(y = \frac{8}{x}\).
The equations for the two graphs are \(y = 8x\) and \(y = \frac{8}{x}\).
Choose the correct answer:
The range of \(y = 2 \sin{\theta} + 1\) is:
3
The range of \(y = 2 \cos{\theta} - 4\) is:
4
The y-intercept of \(2^x + 1\) is:
3
Which of the following passes through \((1;7)\)?
1
|
Previous
6.6 Trigonometric functions
|
Table of Contents |
Next
6.8 Chapter summary
|