Find with reasons, two other angles equal to \(x\).
\(S\hat{R}O = Q\hat{O}R = x\) (alt \(\angle\)s; \(SR \parallel OQ\)).
\(O\hat{R}Q = Q\hat{O}R = x\) (\(\angle\)s opp equal sides).
Therefore \(S\hat{R}O\) and \(O\hat{R}Q\) are both equal to \(x\).
|
Previous
7.2 Triangles
|
Next
7.4 The mid-point theorem
|
A quadrilateral is a closed shape consisting of four straight line segments.
The interior angles of a quadrilateral add up to \(\text{360}\)°.
Mathopenref has some useful simulations on different types of quadrilaterals. Clicking on any of the named quadrilaterals will take you to a page specific to that quadrilateral.
A parallelogram is a quadrilateral with both pairs of opposite sides parallel.
\(ABCD\) is a parallelogram with \(AB\parallel DC\) and \(AD\parallel BC\). Show that:
\(AB=DC\) and \(AD=BC\)
\(\hat{A}=\hat{C}\) and \(\hat{B}=\hat{D}\)
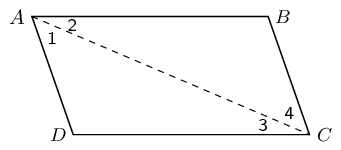
Redraw the diagram and draw line \(AC\).
On your diagram mark all the equal angles.
In \(\triangle ABC\) and \(\triangle CDA\):
\[\begin{array}{rll} {\hat{A}}_{2}& = {\hat{C}}_{3}& \text{(alt }\angle \text{s; } AB\parallel DC\text{)}\\ {\hat{C}}_{4}& = {\hat{A}}_{1}& \text{(alt }\angle \text{s; } BC\parallel AD\text{)} \\ AC & & \text{(common side)} \\ \therefore \triangle ABC & \equiv \triangle CDA & \text{(AAS)} \\ \therefore AB = CD & \text{ and } BC = DA & \end{array}\]\(\therefore\) Opposite sides of a parallelogram have equal length.
We have already shown \({\hat{A}}_{2}={\hat{C}}_{3}\) and \({\hat{A}}_{1}={\hat{C}}_{4}\). Therefore,
\[\hat{A} = {\hat{A}}_{1} + {\hat{A}}_{2} = {\hat{C}}_{3} + {\hat{C}}_{4} = \hat{C}\]Furthermore,
\[\hat{B}=\hat{D} \enspace \left(\triangle ABC\equiv \triangle CDA\right)\]Therefore opposite angles of a parallelogram are equal.
Summary of the properties of a parallelogram:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are equal in length.
Both pairs of opposite angles are equal.
Both diagonals bisect each other.
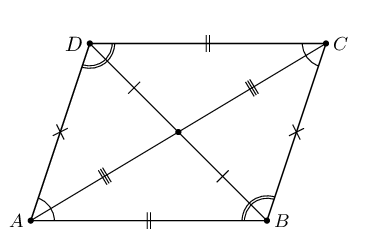
Prove that if both pairs of opposite angles in a quadrilateral are equal, the quadrilateral is a parallelogram.
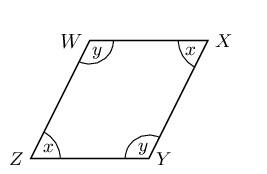
In \(WXYZ\):
\[\begin{array}{rll} \hat{W} = \hat{Y} & =\hat{y} & \text{ (given)} \\ \hat{Z} = \hat{X} & =\hat{x} & \text{ (given)} \\ \hat{W} + \hat{X} + \hat{Y} + \hat{Z} & = 360° & \text{ (sum of }\angle \text{s in a quad)}\\ \therefore 2\hat{x} + 2\hat{y} & =360° & \\ \therefore \hat{x} + \hat{y} & = 180°& \\ \hat{W} + \hat{Z} & = \hat{x} + \hat{y} & \\ & = 180° \end{array}\]But these are co-interior angles between lines \(WX\) and \(ZY\). Therefore \(WX\parallel ZY\).
Similarly \(\hat{W} + \hat{X} = 180°\). These are co-interior angles between lines \(XY\) and \(WZ\). Therefore \(XY\parallel WZ\).
Both pairs of opposite sides of the quadrilateral are parallel, therefore \(WXYZ\) is a parallelogram.
Prove that if both pairs of opposite sides of a quadrilateral are equal, then the quadrilateral is a parallelogram.
Prove that if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Prove that if one pair of opposite sides of a quadrilateral are both equal and parallel, then the quadrilateral is a parallelogram.
A quadrilateral is a parallelogram if:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are equal.
Both pairs of opposite angles are equal.
The diagonals bisect each other.
One pair of opposite sides are both equal and parallel.
\(PQRS\) is a parallelogram. \(PS = OS\) and \(QO = QR\). \(S\hat{O}R = 96^{\circ}\) and \(Q\hat{O}R = x\).
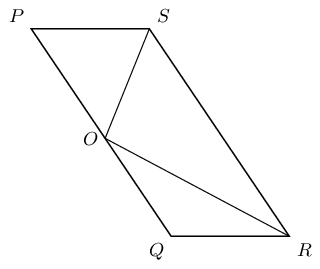
Find with reasons, two other angles equal to \(x\).
\(S\hat{R}O = Q\hat{O}R = x\) (alt \(\angle\)s; \(SR \parallel OQ\)).
\(O\hat{R}Q = Q\hat{O}R = x\) (\(\angle\)s opp equal sides).
Therefore \(S\hat{R}O\) and \(O\hat{R}Q\) are both equal to \(x\).
Write \(\hat{P}\) in terms of \(x\).
Calculate the value of \(x\).
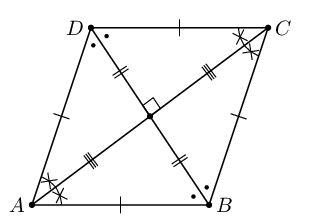
Prove that the diagonals of parallelogram \(MNRS\) bisect one another at \(P\).
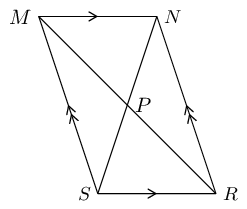
Hint: Use congruency.
First number each angle on the given diagram:
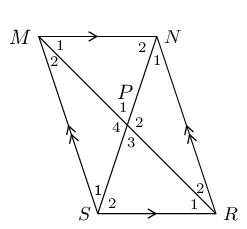
In \(\triangle MNP\) and \(\triangle RSP\):
\begin{align*} \hat{M_1} &= \hat{R_1} \quad \text{(alt } \angle \text{s; } MN \parallel SR\text{)} \\ \hat{P_1} &= \hat{P_3} \quad \text{(vert opp } \angle \text{s } = \text{)} \\ MN & = RS \text{ (opp sides of }\parallel\text{m)} \end{align*}Therefore \(\triangle MNP \equiv \triangle RSP\) (AAS).
Now we know that \(MP = RP\) and therefore \(P\) is the mid-point of \(MR\).
Similarly, in \(\triangle MSP\) and \(\triangle RNP\):
\begin{align*} \hat{M_2} &= \hat{R_2} \quad \text{(alt } \angle \text{s; } MS \parallel NR\text{)} \\ \hat{P_4} &= \hat{P_2} \quad \text{(vert opp } \angle \text{s } = \text{)} \\ MS & = RN \text{ (opp sides of }\parallel\text{m)} \end{align*}Therefore \(\triangle MSP \equiv \triangle RNP\) (AAS).
Now we know that \(NP = SP\) and therefore \(P\) is the mid-point of \(NS\).
Therefore the diagonals of a parallelogram bisect each other.
A rectangle is a parallelogram that has all four angles equal to \(90°\).
A rectangle has all the properties of a parallelogram:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are equal in length.
Both pairs of opposite angles are equal.
Both diagonals bisect each other.
It also has the following special property:
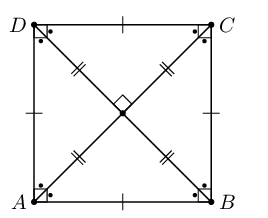
\(PQRS\) is a rectangle. Prove that the diagonals are of equal length.
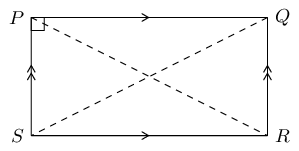
In \(\triangle PSR\) and \(\triangle QRS\):
\[\begin{array}{rll} PS & = QR& \text{(opp sides of rectangle)}\\ SR & & \text{(common side)} \\ P\hat{S}R & = Q\hat{R}S = 90° & \text{ (}\angle \text{s of rectangle)}\\ \therefore \triangle PSR & \equiv \triangle QRS & \text{ (RHS)} \\ \text{Therefore } PR & = QS & \end{array}\]The diagonals of a rectangle are of equal length.
Summary of the properties of a rectangle:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are of equal length.
Both pairs of opposite angles are equal.
Both diagonals bisect each other.
Diagonals are equal in length.
All interior angles are equal to \({90}^{°}\)
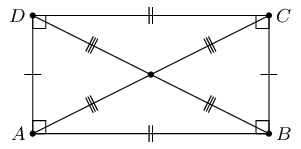
\(ABCD\) is a quadrilateral. Diagonals \(AC\) and \(BD\) intersect at \(T\). \(AC = BD\), \(AT = TC\), \(DT = TB\). Prove that:
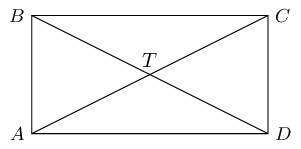
\(ABCD\) is a parallelogram
\(AT = TC\) (given)
\(\therefore DB\) bisects \(AC\) at \(T\)
and \(DT = TB\) (given)
\(\therefore AC\) bisects \(DB\) at \(T\)
therefore quadrilateral \(ABCD\) is a parallelogram (diag of \(\parallel\)m)
\(ABCD\) is a rectangle
\(AC = BD\) (given).
Therefore \(ABCD\) is a rectangle (diags of rectangle).
A rhombus is a parallelogram with all four sides of equal length.
A rhombus has all the properties of a parallelogram:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are equal in length.
Both pairs of opposite angles are equal.
Both diagonals bisect each other.
It also has two special properties:
\(XYZT\) is a rhombus. Prove that:
the diagonals bisect each other perpendicularly;
the diagonals bisect the interior angles.
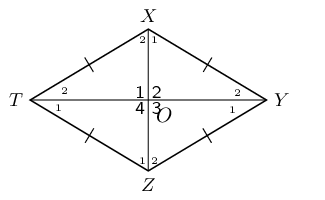
We can further conclude that \({\hat{O}}_{1} = {\hat{O}}_{2} = {\hat{O}}_{3} = {\hat{O}}_{4} = 90°\).
Therefore the diagonals bisect each other perpendicularly.
Therefore diagonal \(XZ\) bisects \(\hat{Z}\). Similarly, we can show that \(XZ\) also bisects \(\hat{X}\); and that diagonal \(TY\) bisects \(\hat{T}\) and \(\hat{Y}\).
We conclude that the diagonals of a rhombus bisect the interior angles.
To prove a parallelogram is a rhombus, we need to show any one of the following:
All sides are equal in length.
Diagonals intersect at right angles.
Diagonals bisect interior angles.
Summary of the properties of a rhombus:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are equal in length.
Both pairs of opposite angles are equal.
Both diagonals bisect each other.
All sides are equal in length.
The diagonals bisect each other at \({90}^{°}\)
The diagonals bisect both pairs of opposite angles.
A square is a rhombus with all four interior angles equal to \(90°\)
OR
A square is a rectangle with all four sides equal in length.
A square has all the properties of a rhombus:
Both pairs of opposite sides are parallel.
Both pairs of opposite sides are equal in length.
Both pairs of opposite angles are equal.
Both diagonals bisect each other.
All sides are equal in length.
The diagonals bisect each other at \(90°\)
The diagonals bisect both pairs of opposite angles.
It also has the following special properties:
All interior angles equal \(90°\).
Diagonals are equal in length.
Diagonals bisect both pairs of interior opposite angles (i.e. all are \(45°\)).
To prove a parallelogram is a square, we need to show either one of the following:
It is a rhombus (all four sides of equal length) with interior angles equal to \(90°\).
It is a rectangle (interior angles equal to \(90°\)).
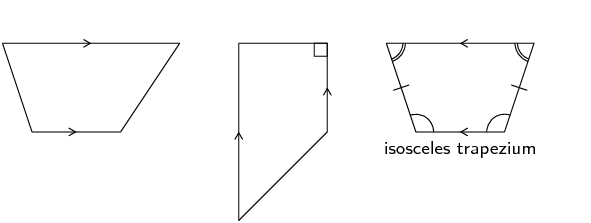
A trapezium is a quadrilateral with one pair of opposite sides parallel.
In British English a trapezium is used to indicate a quadrilateral with one pair of opposite sides parallel while in American English a trapezium is a quadrilateral with no pairs of opposite sides parallel. We will use the British English definition of trapezium in this book.
In British English a trapezoid is used to indicate a quadrilateral with no pairs of opposite sides parallel while in American English a trapezoid is a quadrilateral with one pair of opposite sides parallel.
A trapezium is sometimes called a trapezoid.
Some examples of trapeziums are given below:
A kite is a quadrilateral with two pairs of adjacent sides equal.
\(ABCD\) is a kite with \(AD=AB\) and \(CD=CB\). Prove that:
\(A\hat{D}C=A\hat{B}C\)
Diagonal \(AC\) bisects \(\hat{A}\) and \(\hat{C}\)
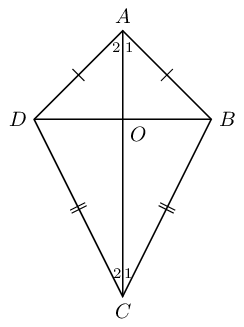
In \(\triangle ADC\) and \(\triangle ABC\):
\[\begin{array}{rll} AD & =AB & \text{(given)} \\ CD & = CB & \text{(given)} \\ AC & & \text{(common side)} \\ \therefore \triangle ADC & \equiv \triangle ABC & \text{(SSS)} \\ \therefore A\hat{D}C & = A\hat{B}C & \end{array}\]Therefore one pair of opposite angles are equal in kite \(ABCD\).
Therefore diagonal \(AC\) bisects \(\hat{A}\) and \(\hat{C}\).
We conclude that the diagonal between the equal sides of a kite bisects the two interior angles and is an axis of symmetry.
Summary of the properties of a kite:
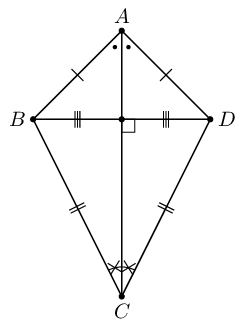
Diagonal between equal sides bisects the other diagonal.
One pair of opposite angles are equal (the angles between unequal sides).
Diagonal between equal sides bisects the interior angles and is an axis of symmetry.
Diagonals intersect at \(90°\)
Use the sketch of quadrilateral \(ABCD\) to prove the diagonals of a kite are perpendicular to each other.
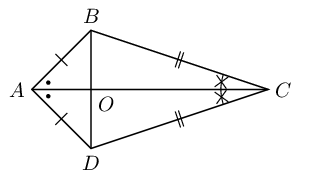
First number the angles:
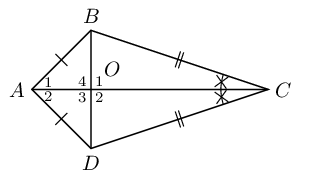
In \(\triangle ADO\) and \(\triangle ABO\):
\[\begin{array}{rll} AD & = AB & \text{(given)} \\ AO & & \text{(common side)} \\ B\hat{A}O & = D\hat{A}O & \text{(given)} \\ \therefore \triangle ADO & \equiv \triangle ABO & \text{(SAS)} \\ \therefore A\hat{B}O & = A\hat{D}O & \end{array}\]In \(\triangle ADB\):
\begin{align*} \text{let } \hat{A_1} & = \hat{A_2} = t \\ \text{and let } A\hat{D}O &= A\hat{B}O = p \\ 2t + 2p &= 180° \quad \text{(sum of }\angle \text{s in} \triangle \text{)} \\ \therefore t + p &= 90° \end{align*}Next we note that:
\begin{align*} \hat{O_1} & = A\hat{B}O + \hat{A_1} \text{ (ext }\angle \text{ of } \triangle \text{)}\\ \hat{O_1} &= p + t \\ &= 90°\\ \therefore AC &\perp BD \end{align*}Therefore the diagonals of a kite are perpendicular to each other.
Explain why quadrilateral \(WXYZ\) is a kite. Write down all the properties of quadrilateral \(WXYZ\).
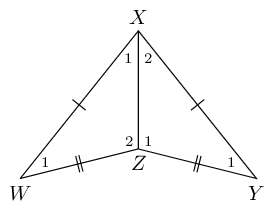
Quadrilateral \(WXYZ\) is a kite because is has two pairs of adjacent sides that are equal in length.
Diagonal between equal sides bisects the other diagonal: \(WP = PY\).
One pair of opposite angles are equal: \(\hat{W_{1}} = \hat{Y_{1}}\).
Diagonal between equal sides bisects the interior angles and is an axis of symmetry: \(\hat{X_1} = \hat{X_2}\).
Diagonals intersect at \(90°\): \(WY \perp PX\).
This video provides a summary of the different types of quadrilaterals and their properties.
Heather has drawn the following diagram to illustrate her understanding of the relationships between the different quadrilaterals. The following diagram summarises the different types of special quadrilaterals.
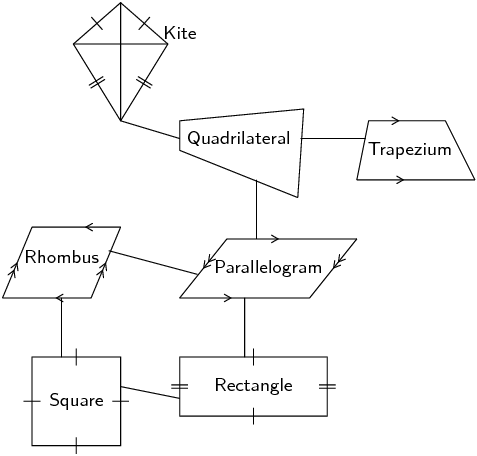
Explain her possible reasoning for structuring the diagram as shown.
Design your own diagram to show the relationships between the different quadrilaterals and write a short explanation of your design.
The following shape is drawn to scale :

Give the most specific name for the shape.
We start by counting the number of sides. There are four sides in this figure and so it is either just a quadrilateral or one of the special types of quadrilateral.
Next we ask ourselves if there are any parallel lines in the figure. You can look at the figure to see if any of the lines look parallel or make a quick sketch of the image and see if any pairs of opposite lines meet at a point.
Both pairs of opposite sides are parallel. This means that the figure can only be one of the following: parallelogram, rectangle, rhombus or square.
Next we ask ourselves if all the interior angles are 90°. All the interior angles are 90° and so this must be a square or a rectangle. Finally we check to see if all the sides are equal in length. In this figure the sides are not equal in length and so it is a rectangle.
Therefore this is a rectangle.
The shape is also a parallelogram and a quadrilateral. This question, however, asked for the most specific name for the shape.
The following shape is drawn to scale :
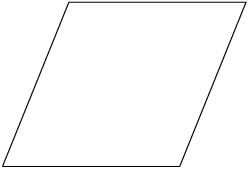
Give the most specific name for the shape.
We start by counting the number of sides. There are four sides in this figure and so it is either just a quadrilateral or one of the special types of quadrilateral.
Next we ask ourselves if there are any parallel lines in the figure. You can look at the figure to see if any of the lines look parallel or make a quick sketch of the image and see if any pairs of opposite lines meet at a point.
Both pairs of opposite sides are parallel. This means that the figure can only be one of the following: parallelogram, rectangle, rhombus or square.
Next we ask ourselves if all the interior angles are 90°. All the interior angles are not 90° and so this must be a parallelogram or a rhombus. Finally we check to see if all the sides are equal in length. In this figure the sides are equal in length and so it is a rhombus.
Therefore this is a rhombus.
The shape is also a parallelogram and a quadrilateral. This question, however, asked for the most specific name for the shape.
Based on the shape that you see list the all the names of the shape. The figure is drawn to scale
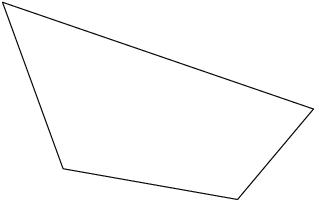
Both pairs of opposite sides are not parallel. This means that the figure can only be some combination of the following: trapezium, kite, or quadrilateral.
The shape is definitely a quadrilateral because it has four sides. It does not have any special properties: it does not have parallel sides, or right angles, or sides which are equal in length. Therefore it is only a quadrilateral.
Based on the shape that you see list the all the names of the shape. The figure is drawn to scale
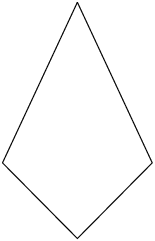
Both pairs of opposite sides are not parallel. This means that the figure can only be some combination of the following: trapezium, kite, or quadrilateral.
The shape is definitely a quadrilateral because it has four sides. It is also a kite because it has two pairs of adjacent sides which are the same lengths. It cannot be a square or a rectangle because it does not have right angles. It cannot be a parallelogram or a trapezium because it does not have any parallel sides. And it is not a rhombus because the four sides are not all the same length.
Therefore the correct answer is: kite and quadrilateral.
Based on the shape that you see list the all the names of the shape. The figure is drawn to scale

Both pairs of opposite sides are parallel. That means that this shape can belong to one or more of these groups: square, rhombus, rectangle or parallelogram.
The given shape is a square. However, it is also a rectangle. A square is also a parallelogram, because it has parallel sides; and it is a rhombus as well, it just happens to have right angles. A square is also a kite, a trapezium and of course a quadrilateral.
Therefore the correct answer is: square, rectangle, rhombus, parallelogram, kite, trapezium and quadrilateral.
Find the area of \(ACDF\) if \(AB = 8,~ BF = 17,~ FE = EC,~ BE = ED,~ \hat{A} = 90^{\circ} ,~ C\hat{E}D = 90^{\circ}\)
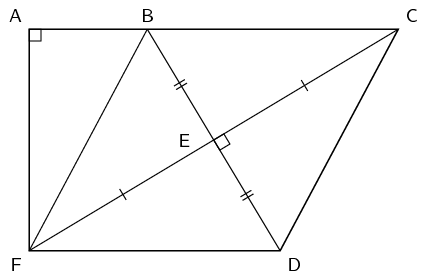
Construct \(G\) such that \(AC = FG\)
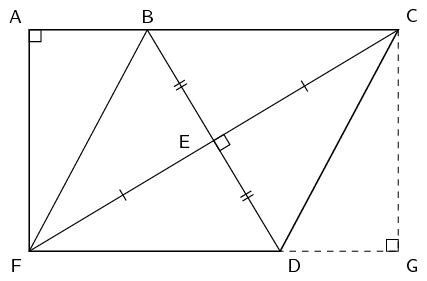
\(BCDF\) is a rhombus (diagonals bisect at right angles)
Since \(BCDF\) is a rhombus \(BC = DF\). We constructed \(G\) such that \(AC = FG\). Therefore \(AB = DG\).
In \(\triangle ABF\) and \(\triangle CGD\):
\begin{align*} B\hat{A}F & = C\hat{G}D = 90^{\circ} \quad \text{(given and by construction)} \\ AB & = DG \quad \text{(by construction)} \\ BF & = CD \quad \text{(} BCDF \text{ is a rhombus)} \end{align*}Therefore \(ABF \equiv CGD\) (RHS)
Therefore \(AF = CG\) and so \(ACGF\) is a rectangle (both pairs of opposite sides equal in length and all interior angles are 90°).
We are given the length of \(AB\) and \(BF\). Since \(\triangle ABF\) is right-angled we can use the theorem of Pythagoras to find the length of \(AF\):
\begin{align*} BF^{2} & = AB^{2} + AF^{2} \\ (17)^{2} & = (8)^{2} + AF^{2} \\ AF^{2} & = 225 \\ AF & = 15 \end{align*}We also know that \(FD = BF = 17\) and so \(AC = 17 + 8 = 25\).
Therefore the area of rectangle \(ACGF\) is:
\begin{align*} A_{\text{rectangle}} & = l \times b \\ & = (25)(15) \\ & = 375 \end{align*}We are almost there. We now need to calculate the area of triangle \(CDG\) and subtract this from the area of the rectangle to get the area of \(ACDF\).
The area of triangle \(CDG\) is:
\begin{align*} A_{\text{triangle}} &= \frac{1}{2} DG \times CG \\ & = \frac{1}{2} (8 \times 15) \\ &= 60 \end{align*}Therefore the area of \(ACDF\) is \(375 - 60 = 315\).
|
Previous
7.2 Triangles
|
Table of Contents |
Next
7.4 The mid-point theorem
|