
4.7 Solving linear inequalities
|
Previous
4.6 Literal equations
|
Next
4.8 Chapter summary
|
4.7 Solving linear inequalities (EMA3H)
A linear inequality is similar to a linear equation in that the largest exponent of a variable is \(\text{1}\). The following are examples of linear inequalities.
\begin{align*} 2x + 2 & \le 1 \\ \frac{2 - x}{3x + 1} & \ge 2 \\ \frac{4}{3}x - 6 & < 7x + 2 \end{align*}The methods used to solve linear inequalities are similar to those used to solve linear equations. The only difference occurs when there is a multiplication or a division that involves a minus sign. For example, we know that \(8>6\). If both sides of the inequality are divided by \(-\text{2}\), then we get \(-4>-3\), which is not true. Therefore, the inequality sign must be switched around, giving \(-4<-3\).
In order to compare an inequality to a normal equation, we shall solve an equation first.
Solve \(2x + 2 = 1\):
\begin{align*} 2x + 2 & = 1 \\ 2x & = 1 - 2 \\ 2x & = -1 \\ x & = -\frac{1}{2} \end{align*}If we represent this answer on a number line, we get:

Now let us solve for \(x\) in the inequality \(2x + 2 \le 1\):
\begin{align*} 2x + 2 & \le 1 \\ 2x & \le 1 - 2 \\ 2x & \le -1 \\ x & \le -\frac{1}{2} \end{align*}If we represent this answer on a number line, we get:

We see that for the equation there is only a single value of \(x\) for which the equation is true. However, for the inequality, there is a range of values for which the inequality is true. This is the main difference between an equation and an inequality.
Remember: when we divide or multiply both sides of an inequality by a negative number, the direction of the inequality changes. For example, if \(x<1\), then \(-x>-1\). Also note that we cannot divide or multiply by a variable.
The following video provides an introduction to linear inequalities.
Interval notation (EMA3J)
Examples:
|
\(\left(4;12\right)\) |
Round brackets indicate that the number is not included. This interval includes all real numbers greater than but not equal to \(\text{4}\) and less than but not equal to \(\text{12}\). |
|
\(\left(-\infty ;-1\right)\) |
Round brackets are always used for positive and negative infinity. This interval includes all real numbers less than, but not equal to \(-\text{1}\). |
|
\(\left[1;13\right)\) |
A square bracket indicates that the number is included. This interval includes all real numbers greater than or equal to \(\text{1}\) and less than but not equal to \(\text{13}\). |
It is important to note that this notation can only be used to represent an interval of real numbers.
We represent the above answer in interval notation as \(\left(-\infty ; -\frac{1}{2}\right]\)
Worked example 17: Solving linear inequalities
Solve for \(r\):
\[6 - r > 2\]Represent the answer on a number line and in interval notation.
Rearrange and solve for \(r\)
\begin{align*} -r & > 2 - 6 \\ -r & > -4 \end{align*}Multiply by \(-\text{1}\) and reverse inequality sign
\[r < 4\]Represent the answer on a number line

Represent the answer in interval notation
\[\left(-\infty ; 4\right)\]Worked example 18: Solving linear inequalities
Solve for \(q\):
\[4q + 3 < 2(q + 3)\]Represent the answer on a number line and in interval notation.
Expand the bracket
\begin{align*} 4q + 3 & < 2(q + 3) \\ 4q + 3 & < 2q + 6 \end{align*}Rearrange and solve for \(q\)
\begin{align*} 4q + 3 & < 2q + 6 \\ 4q - 2q & < 6 - 3 \\ 2q & < 3 \end{align*}Divide both sides by \(\text{2}\)
\begin{align*} 2q & < 3 \\ q & < \frac{3}{2} \end{align*}Represent the answer on a number line

Represent the answer in interval notation
\(\left(-\infty ; \frac{3}{2}\right)\)Worked example 19: Solving compound linear inequalities
Solve for \(x\):
\[5 \le x + 3 < 8\]Represent the answer on a number line and in interval notation.
Subtract \(\text{3}\) from all the parts of the inequality
\[\begin{array}{ccccc} 5 - 3 & \le & x + 3 - 3 & < & 8 - 3 \\ 2 & \le & x & < & 5 \end{array}\]Represent the answer on a number line

Represent the answer in interval notation
\(\left[2 ; 5\right)\)Look at the number line and write down the inequality it represents.

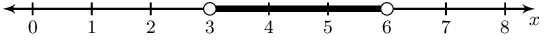
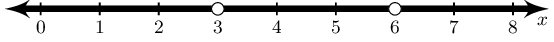

Solve for \(x\) and represent the answer on a number line and in interval notation.
\(3x + 4 > 5x + 8\)
Represented on a number line:

In interval notation: \((-\infty; -2)\)
\(3(x - 1) - 2 \le 6x + 4\)
Represented on a number line:
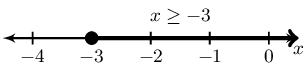
In interval notation: \([-3; \infty)\)
\(\dfrac{x - 7}{3} > \dfrac{2x - 3}{2}\)
Represented on a number line:

In interval notation: \((-\infty; -\frac{5}{4})\)
\(-4(x - 1) < x + 2\)
Represented on a number line:
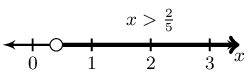
In interval notation: \((\frac{2}{5}; \infty)\)
\(\dfrac{1}{2}x + \dfrac{1}{3}(x - 1) \ge \dfrac{5}{6}x - \dfrac{1}{3}\)
The inequality is true for all real values of \(x\).
\(-2 \le x - 1 < 3\)
Represented on a number line:
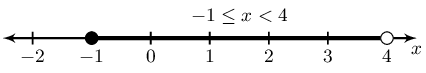
In interval notation: \([-1; 4)\)
\(-5 < 2x - 3 \le 7\)
Represented on a number line:
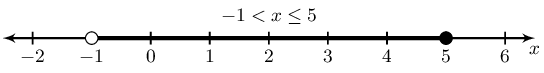
In interval notation: \((-1; 5]\)
\(7(3x + 2) - 5(2x - 3) > 7\)
Represented on a number line:

In interval notation: \((-2; \infty)\)
\(\dfrac{5x - 1}{-6} \ge \dfrac{1 - 2x}{3}\)
Represented on a number line:
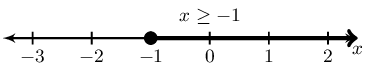
In interval notation: \([-1; \infty)\)
\(3 \le 4 - x \le 16\)
Represented on a number line:
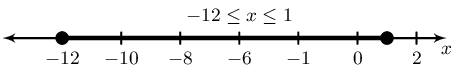
In interval notation: \([1; 12]\)
\(\dfrac{-7y}{3} - 5 > -7\)
Represented on a number line:
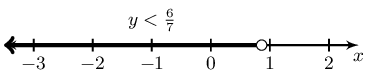
In interval notation: \((-\infty;\frac{6}{7})\)
\(1 \le 1 - 2y < 9\)
Represented on a number line:
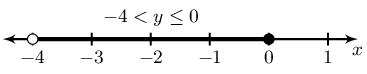
In interval notation: \((-4;0]\)
\(-2 < \dfrac{x - 1}{-3} < 7\)
Represented on a number line:
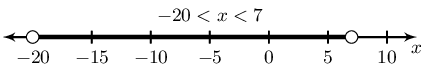
In interval notation: \((-20;7)\)
Solve for \(x\) and show your answer in interval notation:
\(2x -1 < 3(x+11)\)
\begin{align*} 2 x -1 &< 3(x +11) \\ 2 x -1 &< 3 x +33 \\ 2 x -3 x &< 33 +1 \\ -1 x &< 34 \\ \therefore x &> -34 \end{align*}
\[\left(-34;\infty\right)\]
\(x -1 < -4(x-6)\)
\begin{align*} x -1 &< -4(x -6) \\ x -1 &< -4 x +24 \\ x +4 x &< 24 +1 \\ 5 x &< 25 \\ \therefore x &< 5 \end{align*}
\[\left(-\infty;5\right)\]
\(\dfrac{x-1}{8} \leq \dfrac{2(x-2)}{3}\)
\(\; x \in \left[ \frac{29}{13} ;\infty\right)\).
\(\dfrac{x+2}{4} \leq \dfrac{-2(x-4)}{7}\)
\(\; x \in \left(-\infty; \frac{6}{5} \right]\).
\(\dfrac{1}{5}x - \dfrac{5}{4}(x+2) > \dfrac{1}{4}x + 3\)
\begin{align*} \frac{1}{5}x - \frac{5}{4}(x+2) &> \frac{1}{4}x +3 \\ 4x - 25(x+2) &> 5x +60 \\ 4x - 25 x-50 &> 5x +60 \\ 4x - 25 x -5x &> 60 + 50\\ -26x &> 110\\ \therefore x &< -\frac{55}{13} \end{align*}
The interval is: \[\left(-\infty;-\frac{55}{13}\right)\]
\(\dfrac{1}{5}x - \dfrac{2}{5}(x+3) \geq \dfrac{4}{2}x +3\)
\begin{align*} \frac{1}{5}x - \frac{2}{5}(x+3) &\geq \frac{4}{2}x +3 \\ 2x - 4(x+3) &\geq 20x +30 \\ 2x - 4 x-12 &\geq 20x +30 \\ 2x - 4 x -20x &\geq 30 + 12\\ -22x &\geq 42\\ \therefore x &\leq -\frac{21}{11} \end{align*}
The interval is: \[\left(-\infty;-\frac{21}{11}\right]\]
\(4x +3 < -3 \quad\text{or}\quad 4x +3 > 5\)
Solve the inequality: \[\begin{array}{rclcrcl} 4x +3 &<& -3 &\text{or}& 4x +3 &>& 5 \\ 4x &<& -3-3 &\text{or}& 4x &>& 5-3 \\ x &<& \frac{-3-3}{4} &\text{or}& x &>& \frac{5-3}{4} \\ x &<& - \frac{3}{2} &\text{or}& x &>& \frac{1}{2} \\ \end{array}\]
\[\left(-\infty; - \frac{3}{2}\right) \cup \left(\frac{1}{2}; \infty\right)\]
\(4 \ge -6x -6 \ge -3\)
Solve the inequality: \[\begin{array}{rcccl} 4 &\ge& -6x -6 &\ge& -3 \\ 4+6 &\ge& -6x &\ge& -3+6 \\ \frac{4+6}{-6} &\le& x &\le& \frac{-3+6}{-6} \\ - \frac{5}{3} &\le& x &\le& - \frac{1}{2} \\ \end{array}\]
\[\left[- \frac{5}{3}; - \frac{1}{2}\right]\]
Solve for the unknown variable and show your answer on a number line.
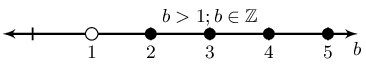
However we are told that \(a \in \mathbb{N}\) and so \(a > 0\).
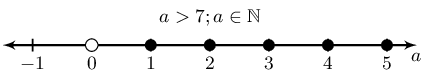
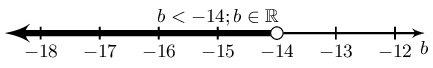
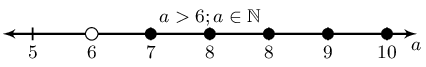
|
Previous
4.6 Literal equations
|
Table of Contents |
Next
4.8 Chapter summary
|
