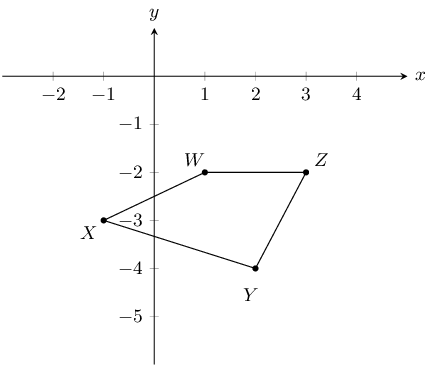
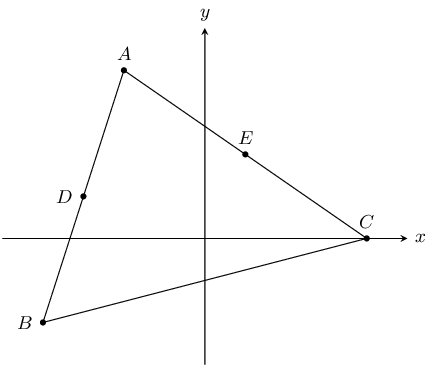
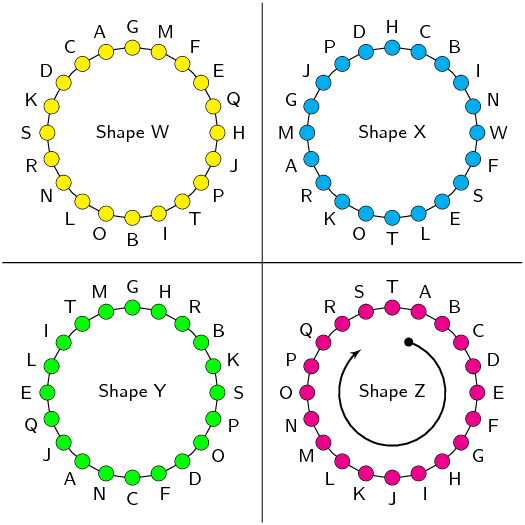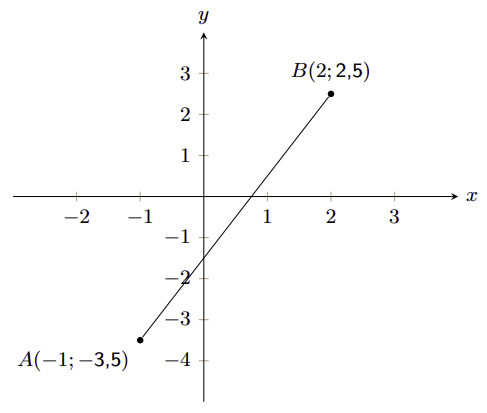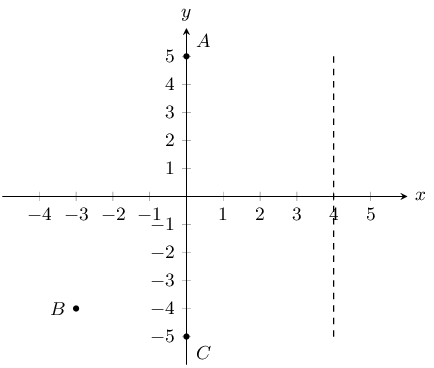You are given the following diagram, with various points shown:

Find the coordinates of points \(A\), \(B\), \(C\), \(D\) and \(E\).
From the graph we can read off the \(x\) and \(y\) values for each point.
\(A(7;-4)\), \(B(3;-3)\), \(C(7;7)\), \(D(-2;-8)\) and \(E(-5;4)\)
You are given the following diagram, with various points shown:

Which point lies at the coordinates \((3;-5)\)?
For this question, we are must find point \((3;-5)\).
Therefore, on the graph we can trace the \(x\) and \(y\) values.
Therefore, point \(A\) lies at the coordinates: \((3;-5)\)
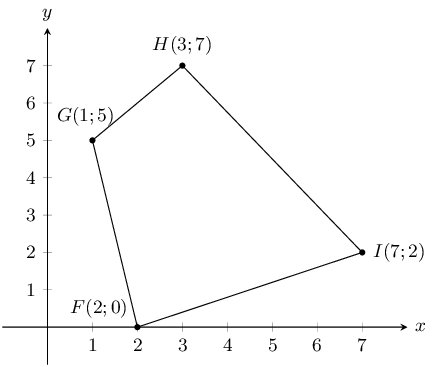
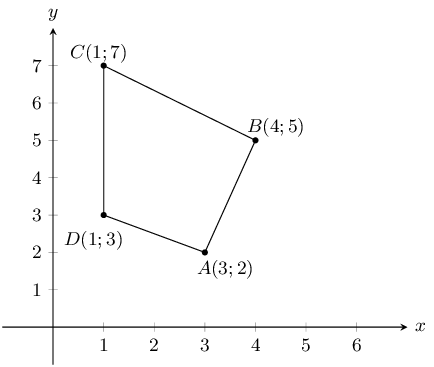
You are given the following diagram, with 4 shapes drawn.
All the shapes are identical, but each shape uses a different naming convention:
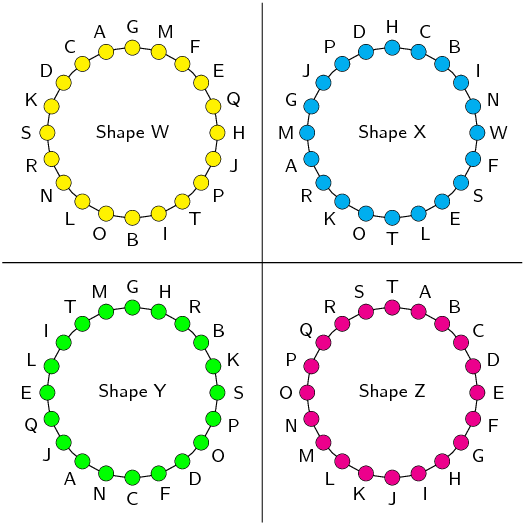
Which shape uses the correct naming convention?
We recall that the correct naming convention for a shape is in alphabetical order, either
clockwise or anti-clockwise around the shape.
From the diagram, we can see that only Shape Z sticks to this naming convention.
You are given the following diagram:
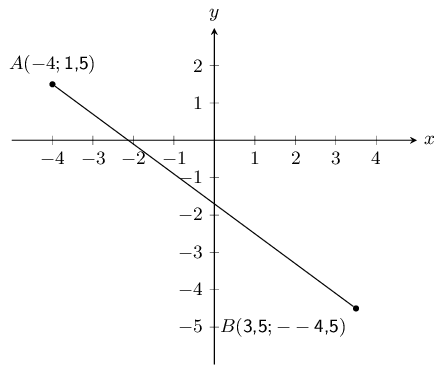
Calculate the length of line \(AB\), correct to 2 decimal places.
The equation for distance is \(d_{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\). We substitute in
\(A(-4;\text{1,5})\) and \(B(\text{3,5};-\text{4,5})\) and solve:
\(\begin{aligned}
d_{AB} & = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\\
& = \sqrt{(\text{3,5} - (-\text{4}))^2 + (-\text{4,5} - (\text{1,5}))^2} \\
& = \sqrt{(\text{3,5} + \text{4})^2 + (-\text{4,5} - \text{1,5})^2} \\
& = \sqrt{(\text{7,5})^2 + (-\text{6})^2} \\
& = \sqrt{(\text{56,25}) + (\text{36})} \\
& = \sqrt{(\text{92,25})} \\
& = \text{9,81}
\end{aligned}\)
The following picture shows two points on the Cartesian plane, \(A\) and \(B\).
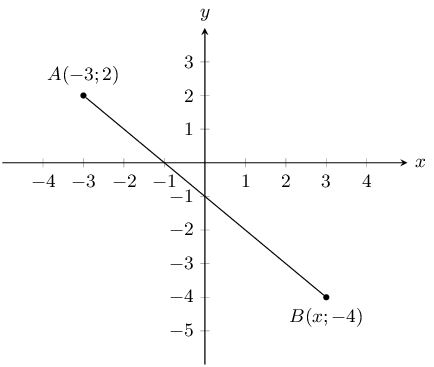
The distance between the points is \(\text{8,4853}\). Calculate the missing coordinate of point \(B\).
The equation for distance is \(d_{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\). We substitute in
\(A(-\text{3};\text{2})\) and \(B(x;-\text{4})\):
\(\begin{aligned}
d_{AB} & = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\\
\text{8,4853} & = \sqrt{(x - (-\text{3}))^2 + (-\text{4} - (\text{2}))^2} \\
\text{8,4853} & = \sqrt{(x \text{+3})^2 + (-\text{4} -\text{2})^2} \\
\end{aligned}\)
Now we re-arrange, and solve for the value of \(x\):
\(\begin{aligned}
(\text{8,4853})^2 & = (x \text{+3})^2 + (-\text{4} -\text{2})^2 \\
\text{72} & = (x \text{+3})^2 + (-\text{4} -\text{2})^2 \\
\text{72} & = (x\text{+3})^2 \text{+36} \\
(x+3)^2 & = \text{36} \\
x \text{+3} & = \pm \sqrt{\text{36}} \\
x & = \pm \text{6} -\text{3} \\
x & = (\text{3}) \text{ or }(-\text{9}) \\
\end{aligned}\)
We now have a choice between 2 values for \(x\). From the diagram we can see that the appropriate value for
this question is \(\text{3}\).
You are given the following diagram:
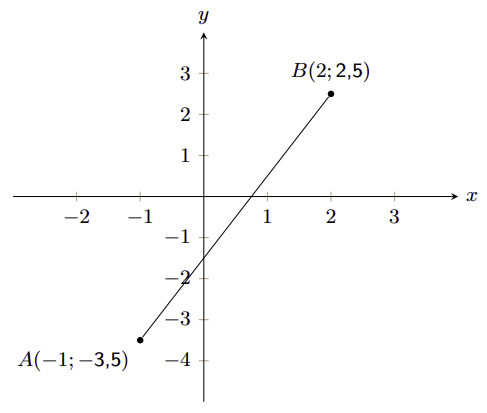
Calculate the gradient (\(m\)) of line \(AB\). The coordinates are \(A (-1;-\text{3,5})\) and \(B
(2;\text{2,5})\) respectively.
\(\begin{aligned}
m & = \left( \frac{y_B - y_A}{x_B - x_A} \right) \\
& = \left( \frac{(\text{2,5}) - (-\text{3,5})}{(\text{2}) - (-\text{1})} \right) \\
& = \text{2}
\end{aligned}\)
Therefore the gradient, \(m\), of the line \(AB\) is \(\text{2}\).
You are given the following diagram:

You are also told that line \(AB\) has a gradient, \(m\), of \(\text{0,5}\).
Calculate the missing co-ordinate of point \(B\).
\begin{align*}
m & = \left( \frac{y_B - y_A}{x_B - x_A} \right) \\
\text{0,5} & = \left(\frac{(\text{3,5}) - (\text{0,5})}{x - (-\text{2})} \right) \\
\text{0,5}(x + \text{2}) & = \text{3} \\
x + \text{2} & = \text{6} \\
x & = \text{4}
\end{align*}
You are given the following diagram:
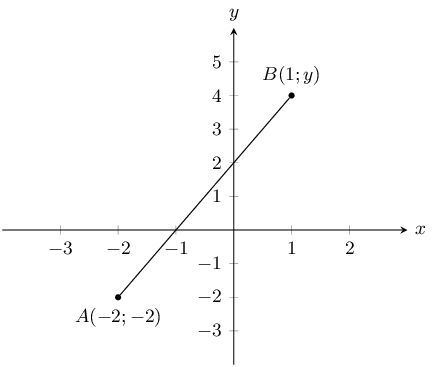
You are also told that line \(AB\) has a gradient, \(m\), of \(\text{2}\).
Calculate the missing co-ordinate of point \(B\).
\begin{align*}
m & = \left( \frac{y_B - y_A}{x_B - x_A} \right) \\
\text{2} & = \left(\frac{y - (-\text{2})}{(\text{1}) - (-\text{2})} \right) \\
\text{2}(\text{3}) & = y + \text{2} \\
\text{6} & = y + \text{2} \\
\text{4} & = y
\end{align*}
You are given the following diagram:
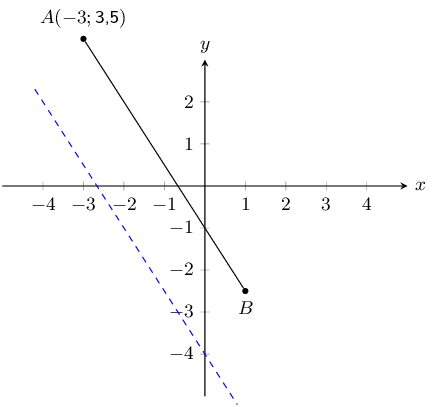
You are also told that line \(AB\) runs parallel to the following line: \(y = -\text{1,5}x - \text{4}\).
Point \(A\) is at \(\left(-3 ; \text{3,5} \right)\).
Find the equation of the line \(AB\).
Let \(y = -\text{1,5}x - \text{4}\) be line \(CD\).
Since line \(AB\) is parallel to line \(CD\), \(m_{AB} = m_{CD} = -\text{1,5}\).
Now we can substitute in the known point (\(A\)) and find the \(y\)-intercept of the line:
\begin{align*}
y & = -\text{1,5}x + c \\
(\text{3,5}) & = (-\text{1,5})(-\text{3}) + c \\
c & = -\text{1}
\end{align*}
Therefore, the equation of the line \(AB\) is: \(y = -\text{1,5} x - \text{1}\)
You are given the following diagram:
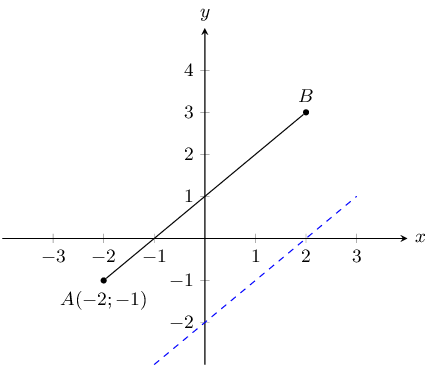
You are also told that line \(AB\) runs parallel to the following line: \(y = x - 2\).
Calculate the missing co-ordinate of point \(B(x;3)\).
Let \(y = x - 2\) be line \(CD\).
Since line \(AB\) is parallel to line \(CD\), \(m_{AB} = m_{CD} = 1\).
Now we can substitute in the known point (\(A\)) and find the \(y\)-intercept of the line:
\begin{align*}
y & = x + c \\
-1 & = -2 + c \\
c & = 1
\end{align*}
Therefore, the equation of the line \(AB\) is: \(y = x + 1\).
Finally, we substitute the known value for point \(B\) into the equation for line \(AB\):
\begin{align*}
y & = x + 1 \\
3 & = x + 1 \\
2 & = x
\end{align*}
Therefore point \(B\) is at \((2;3)\).
You are given the following diagram:
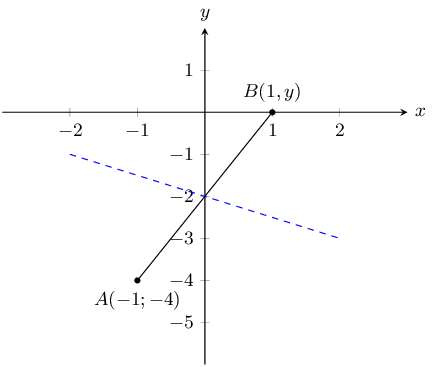
You are also told that line \(AB\) runs perpendicular to the following line: \(y = -\text{0,5}x -
\text{2}\).
Calculate the missing co-ordinate of point \(B\).
The general form of a straight line is: \(y = mx + c\).
Let line \(CD\) be \(y = -\text{0,5}x - 2\).
Line \(AB\) is perpendicular to line \(CD\) and so \(m_{AB} = \dfrac{-1}{m_{CD}}\).
\begin{align*}
y & = mx + c \\
y & = \left(\frac{-1}{m_{CD}}\right)x + c \\
y & = \left(\frac{-1}{-\text{0,5}}\right)x + c \\
y & = 2x + c
\end{align*}
Now we can substitute point \(A\) into the equation to find the \(y\)-intercept:
\begin{align*}
y & = \text{2}x + c \\
-\text{4} & = (\text{2})(-\text{1}) + c \\
c & = -\text{2}
\end{align*}
Next we can substitute in point \(B\) to find the missing coordinate:
\begin{align*}
y & = \text{2}x - \text{2} \\
y & = (\text{2})(\text{1}) - \text{2} \\
y & = \text{0}
\end{align*}
Therefore the missing coordinate is \(B(1;0)\).
The graph here shows line, \(AB\). The blue dashed line is perpendicular to \(AB\).
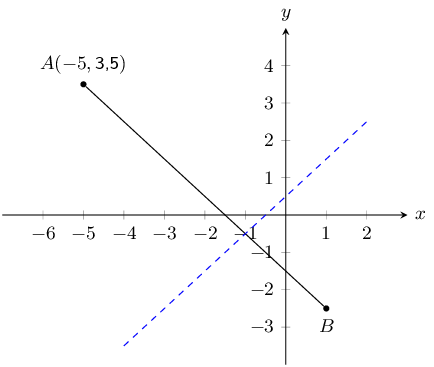
The equation of the blue dashed line is \(y = x + \text{0,5}\). Point \(A\) is at \((-\text{5};
\text{3,5})\).
Determine the equation of line \(AB\).
Let line \(CD\) be the blue dashed line.
Line \(AB\) is perpendicular to line \(CD\) and so \(m_{AB} = \dfrac{-1}{m_{CD}}\).
\begin{align*}
y & = mx + c \\
y & = \left(\frac{-1}{m_{CD}}\right)x + c \\
y & = \left(\frac{-1}{1}\right)x + c \\
y & = -x + c
\end{align*}
Now we can substitute point \(A\) into the equation to find the \(y\)-intercept:
\begin{align*}
y & = -x + c \\
\text{3,5} & = (-\text{1})(-\text{5}) + c \\
c & = -\text{1,5}
\end{align*}
Therefore the equation of line \(AB\) is: \(y = -x - \text{1,5}\).
You are given the following diagram:
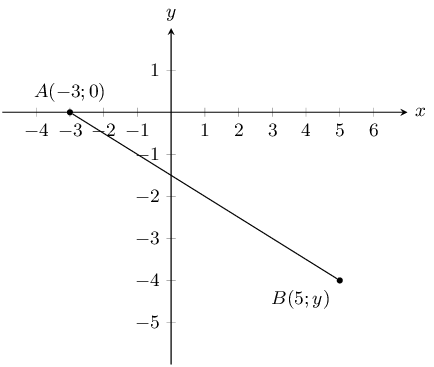
You are also told that line \(AB\) has the following equation: \(y = -\text{0,5} x - \text{1,5}\).
Calculate the missing co-ordinate of point \(B\).
We can substitute the known value for point \(B\) into the given equation for line \(AB\):
\begin{align*}
y & = (-\text{0,5})x - \text{1,5} \\
y & = (-\text{0,5})(\text{5}) - \text{1,5} \\
y & = -\text{4}
\end{align*}
You are given the following diagram:
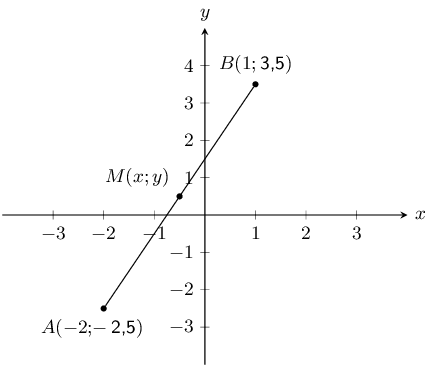
Calculate the coordinates of the mid-point (\(M\)) between point \(A (-\text{2};-\text{2,5})\) and point
\(B (\text{1};\text{3,5})\) correct to 1 decimal place.
\begin{align*}
M(x;y) & = \left( \frac{x_A + x_B}{2} ; \frac{y_A + y_B}{2} \right) \\
& = \left( \frac{(-\text{2}) + (\text{1})}{2} ; \frac{(-\text{2,5}) + (\text{3,5})}{2} \right) \\
M(x;y) & = \left(-\text{0,5} ; \text{0,5} \right)
\end{align*}
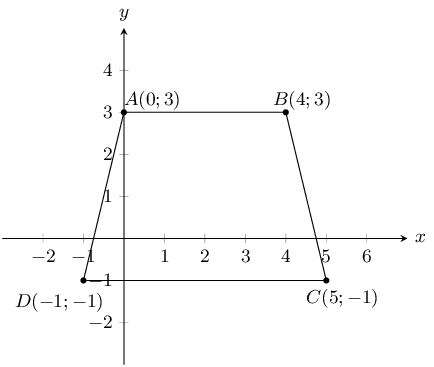
\(A(-2;3)\)and \(B(2;6)\) are points in the Cartesian plane. \(C(a;b)\) is the mid-point of \(AB\). Find
the values of \(a\) and \(b\).
\begin{align*}
M_{AB} &= \left(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\right)\\
&= \left(\frac{-2-2}{2};\frac{3+6}{2}\right)\\
(a;b) &= \left(0;\frac{9}{2}\right)\\
\therefore a=0 &\text{ and }b=\frac{9}{2}
\end{align*}
passing through \(P(5; 5)\) and \(Q(-2; 12)\).
\begin{align*}
m &= \frac{y_2-y_1}{x_2-x_1} \\
m_{PQ} &= \frac{12-5}{-2-5} \\
&= \frac{7}{-7} \\
m_{PQ} &= -1 \\ \\
y &= mx + c \\
(5) &= (-1)(5) + c \\
c &= 5+5 \\
c &= 10\\
\therefore y &= -x + 10
\end{align*}
parallel to \(y = 3x +4\) and passing through \((4; 0)\).
\begin{align*}
m &= 3 \text{ (parallel lines)} \\
y &= mx + c \\
(0) &= (3)(4) + c \\
c &= 12\\
\therefore y &= 3x + 12
\end{align*}
passing through \(F(2; 1)\) and the mid-point of \(GH\) where \(G(-6; 3)\) and \(H(-2; -3)\).

\begin{align*}
M(x;y) &= (\frac{x_1 + x_2}{2}; \frac{y_1 + y_2}{2}) \\
M_{GH} &= (\frac{-6+(-2)}{2}; \frac{3 + (-3)}{2}) \\
M_{GH} &= (-4; 0) \\ \\
(y -y_1) &= m(x -x_1) \\
m &= \frac{y_2-y_1}{x_2-x_1} \\ \\
(y - 0) &= \frac{1-0}{2-(-4)}(x - (-4)) \\
\therefore y &= \frac{1}{6}(x + 4) \\
\therefore y &= \frac{1}{6}x + \frac{2}{3}
\end{align*}
\(EFGH\) is a parallelogram with vertices \(E(-1;2)\), \(F(-2;-1)\) and \(G(2;0)\). Find the coordinates of
\(H\) by using the fact that the diagonals of a parallelogram bisect each other.
Since the diagonal bisect each other the mid-point of \(EG\) is equal to the mid-point of \(FH\). We can
first calculate the mid-point of \(EG\) since we have the co-ordinates of both \(E\) and \(G\). We can then
use that mid-point to help us find the co-ordinates of \(H\).
\begin{align*}
M_{EG} &= \left(\frac{x_1 + x_2}{2} ; \frac{y_1 + y_2}{2}\right) \\
&= \left(\frac{-1 + 2}{2} ; \frac{2 + 0}{2}\right) \\
&= \left(\frac{1}{2} ; 1\right) \\\\
M_{FH} &= \left(\frac{x_1 + x_2}{2} ; \frac{y_1 + y_2}{2}\right) \\
&= \left(\frac{-2 + x}{2} ; \frac{-1 + y}{2}\right) \\
\left(\frac{1}{2} ; 1\right) &= \left(\frac{-2 + x}{2} ; \frac{-1 + y}{2}\right)
\end{align*}
Solve for \(x\):
\begin{align*}
\frac{1}{2} &= \frac{-2+x}{2} \\
1 &= -2+x\\
x &= 3
\end{align*}
Solve for \(y\):
\begin{align*}
1 &= \frac{-1+y}{2} \\
2 &= -1+y \\
y &= 3
\end{align*}
Therefore \(H(3;3)\).
\(\triangle PQR\) has vertices \(P(1;8)\), \(Q(8;7)\) and \(R(7;0)\). Show through calculation that
\(\triangle PQR\) is a right angled isosceles triangle.
First draw a sketch:
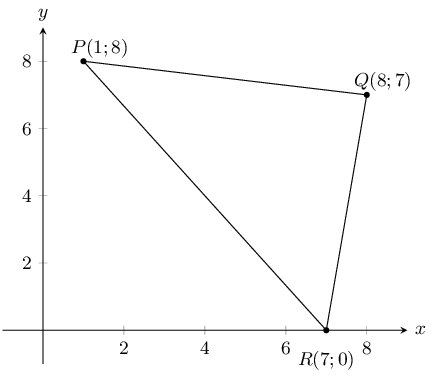
Next calculate the gradient of each of the three sides of the triangle:
\begin{align*}
m_{PQ} &= \frac{8 - 7}{1 - 8} \\
&= -\frac{1}{7} \\\\
m_{QR} &= \frac{7 - 0}{8 - 7} \\
&= \frac{7}{1} \\\\
m_{PR} &= \frac{8 - 0}{1 - 7} \\
&= -\frac{4}{3}
\end{align*}
Now we can check \(m_{PQ} \times m_{QR}\), \(m_{QR} \times m_{PR}\) and \(m_{PQ} \times m_{PR}\). As soon
as we find one of these values is equal to \(-\text{1}\) then we have proved that the triangle is
right-angled.
\begin{align*}
m_{PR} \times m_{QR} &= -\frac{1}{7} \times \frac{7}{1}\\
&= -1
\end{align*}
Therefore \(\triangle PQR\) is right-angled, \(PR \perp QR\). The right-angle is \(P\hat{Q}R\).
Finally we calculate the lengths of sides \(PQ\) and \(RQ\) to show that the triangle is isosceles. We do
not need to calculate \(PR\) as this is the hypotenuse of the triangle and must be longer than \(PQ\) and
\(RQ\).
\begin{align*}
PQ &= \sqrt{(1 - 8)^2 + (8 - 7)^2} \\
&= \sqrt{49 + 1} \\
&= \sqrt{50} \\\\
RQ &= \sqrt{(8 - 7)^2 + (7 - 0)^2} \\
&= \sqrt{1 + 49} \\
&= \sqrt{50}
\end{align*}
Therefore \(PQ = RQ\) and therefore \(\triangle PQR\) is a right-angled, isosceles triangle.
\(\triangle ABC\) has vertices \(A(-3;4)\), \(B(3;-2)\) and \(C(-5;-2)\). \(M\) is the mid-point of \(AC\)
and \(N\) is the mid-point of \(BC\). Use \(\triangle ABC\) to prove the mid-point theorem using analytical
geometry methods.
First draw a sketch:
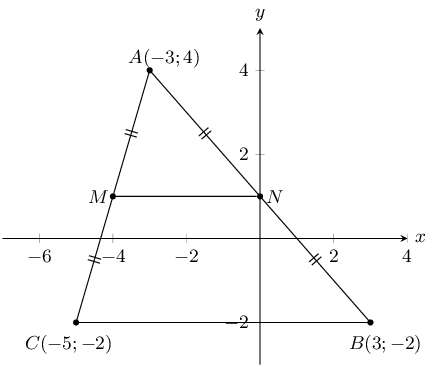
The mid-point theorem states that the line joining the mid-points of two sides of a triangle is parallel to
the third side and equal to half the length of the third side. Therefore we need to show that \(MN \parallel
BC\) and that \(MN = \frac{1}{2} BC\).
We need to calculate the co-ordinates of mid-points \(M\) and \(N\):
\begin{align*}
M &= \left(\frac{-3 - 5}{2} ; \frac{4 - 2}{2}\right)\\
&= (-4;1)\\
N &= \left(\frac{-3 + 3}{2} ; \frac{4 - 2}{2}\right)\\
&= (0;1)
\end{align*}
Now we can show that \(MN \parallel BC\):
\begin{align*}
m & = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\\\
m_{BC} &= \frac{-2 - (-2)}{3 - (-5)}\\
& = 0 \\\\
m_{MN} &= \frac{1 - 1}{-4 - 0}\\
& = 0 \\\\
\therefore MN & \parallel BC
\end{align*}
Finally we can use the distance formula to show that \(MN = \frac{1}{2}BC\):
\begin{align*}
d & = \sqrt{(y_{2} - y_{1})^{2} + (x_{2} - x_{1})^{2}} \\
d_{MN} & = \sqrt{(1 - 1)^{2} + (-4 - 0)^{2}} \\
& = 4 \\
d_{BC} & = \sqrt{(-2 - (-2))^{2} + (-5 - 3)^{2}} \\
& = 8 \\
\therefore MN &= \frac{1}{2}CB
\end{align*}
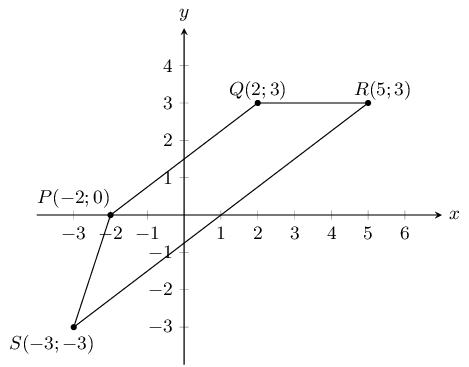
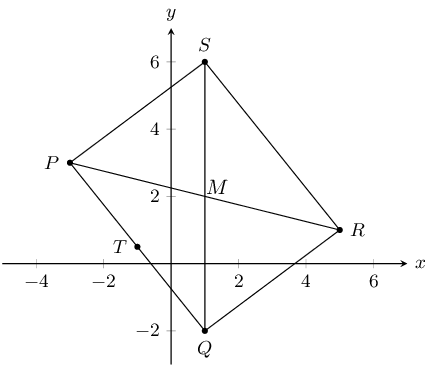
Calculate the length of \(PQ\).
\begin{align*}
PQ & = \sqrt{(-3 - 1)^{2} + (3 + 2)^{2}} \\
& = \sqrt{41}
\end{align*}
Find the coordinates of \(M\) where the diagonals meet.
\(M\) is the mid-point of both \(PR\) and \(QS\) (\(PQRS\) is a parallelogram). Since we do not know the
coordinates of \(S\) we will use \(PR\) to find \(M\).
\begin{align*}
M\left(\frac{-3 + 5}{2}; \frac{3 + 1}{2}\right) \\
\therefore M(1;2)
\end{align*}
Find \(T\), the mid-point of \(PQ\).
\begin{align*}
T\left(\frac{-3 + 1}{2}; \frac{3 - 2}{2}\right) \\
\therefore T\left(-1;\frac{1}{2}\right)
\end{align*}
Show that \(MT \parallel QR\).
\begin{align*}
m_{MT} & = \frac{2 - \frac{1}{2}}{1 + 1} \\
& = \frac{3}{4} \\\\
m_{QR} & = \frac{-2 - 1}{1 - 4} \\
& = \frac{3}{4} \\\\
\therefore m_{MT} & = m_{QR} \\
\therefore MT \parallel QR
\end{align*}
Calculate the coordinates of \(S\).
We can use the coordinates of \(M\) to find the coordinates of \(S\):
\[M(1;2) = S\left(\frac{x + 1}{2}; \frac{y - 2}{2}\right)\]
Solve for \(x\):
\begin{align*}
1 & = \frac{x + 1}{2} \\
2 & = x + 1 \\
x & = 1
\end{align*}
Solve for \(y\):
\begin{align*}
2 & = \frac{y - 2}{2} \\
4 & = y - 2 \\
y & = 6
\end{align*}
Therefore \(S(1;6)\).
Through calculation, determine whether the triangle is equilateral, isosceles or scalene. Be sure to show
all your working.
\begin{align*}
PQ & = \sqrt{(5 - 1)^{2} + (1 - 3)^{2}} \\
& = 2\sqrt{5} \\\\
QR & = \sqrt{(1 - 1)^{2} + (3 + 2)^{2}} \\
& = 5 \\\\
PR & = \sqrt{(5 - 1)^{2} + (1 + 2)^{2}} \\
& = 5 \\\\
\therefore QR & = PR \text{ triangle is isosceles}
\end{align*}
\(\triangle PQR\) is an isosceles triangle.
Find the coordinates of points \(S\) and \(T\), the mid-points of \(PQ\) and \(QR\).
\begin{align*}
S\left(\frac{5+1}{2}; \frac{1+3}{2}\right) \\
\therefore S(3;2) \\\\
T\left(\frac{1+1}{2}; \frac{3-2}{2}\right) \\
\therefore T\left(1;\frac{1}{2}\right)
\end{align*}
Determine the gradient of the line \(ST\).
\begin{align*}
m_{ST} & = \frac{2 - \frac{1}{2}}{3 - 1} \\
& = \frac{\frac{3}{2}}{2} \\
& = \frac{3}{4}
\end{align*}
Prove that \(ST \parallel PR\).
\begin{align*}
m_{PR} & = \frac{1 + 2}{5 - 1} \\
& = \frac{3}{4} \\
\therefore ST \parallel PR & \text{ (equal gradients)}
\end{align*}
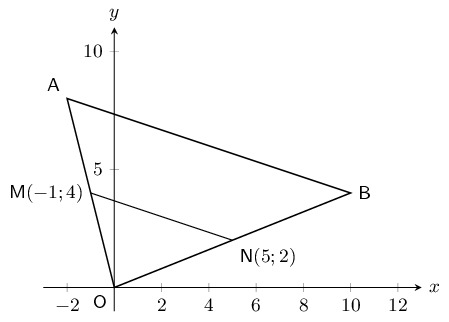
the coordinates of \(B\).
\begin{align*}
M(x;y) &= (\frac{x_1 + x_2}{2}; \frac{y_1 + y_2}{2}) \\
(2;-2)&= (\frac{3 + x_B}{2}; \frac{1 + y_B}{2}) \\ \\
2 &= \frac{3 + x_B}{2} \\
4 &= 3 + x_B \\
x_B & = 1 \\ \\
-2 &= \frac{1 + y_B}{2} \\
-4 &= 1 + y_B \\
y_B &= -5 \\ \\
\therefore B(x;y) &= (1;-5)
\end{align*}
\begin{align*}
m &= \frac{y_2-y_1}{x_2-x_1} \\
m_{AM} &= \frac{-2-1}{2-3} \\
&= \frac{-3}{-1} \\
&= 3
\end{align*}
the equation of the line \(AM\).
\begin{align*}
y &= mx + c \\
(-2) &= (3)(2) + c \\
c &= -2 - 6 \\
c &= -8 \\ \\
\therefore y &= 3x -8
\end{align*}
the perpendicular bisector of \(AB\).
The perpendicular bisector of \(AB\) passes through \(M\) and has a gradient \(-\dfrac{1}{m_{AB}}\).
\begin{align*}
m &= -\frac{1}{m_{AB}} \\
m &= -\frac{1}{3} \\ \\
y &= mx + c \\
(-2) &= (-\frac{1}{3})(2) + c \\
c &= \frac{2}{3} -2 \\
c &= -\frac{4}{3}\\
\therefore y &= -\frac{1}{3}x -\frac{4}{3}
\end{align*}
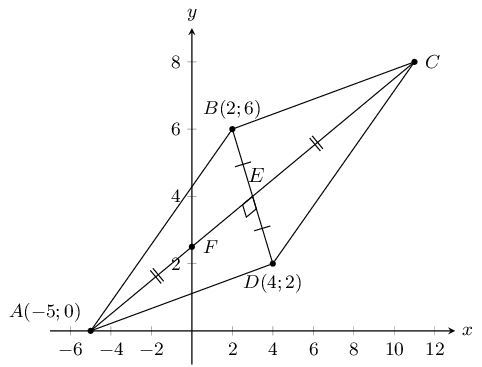
Determine the coordinates of \(E\), the mid-point of \(BD\).
\begin{align*}
M(x;y) &= \left(\frac{x_1 + x_2}{2}; \frac{y_1 + y_2}{2}\right) \\
E &= \left(\frac{5 + (-4)}{2}; \frac{0 + (-3)}{2}\right) \\
\therefore E &= \left(\frac{1}{2}; -\frac{3}{2}\right)
\end{align*}
Prove that \(ABCD\) is a parallelogram.
\begin{align*}
M(x;y) &= \left(\frac{x_1 + x_2}{2}; \frac{y_1 + y_2}{2}\right) \\
M_{AC} &= \left(\frac{-3 + 4}{2}; \frac{6 + (-9)}{2}\right) \\
&= \left(\frac{1}{2}; -\frac{3}{2}\right) \\
\therefore M_{AC} &= E
\end{align*}
\(ABCD\) is a parallelogram (Diagonals bisect at \(E\)).
Find the equation of diagonal \(BD\).
\begin{align*}
(y -y_1) &= m(x -x_1) \\
m &= \frac{y_2-y_1}{x_2-x_1} \\ \\
(y - 0) &= \frac{-3-0}{-4-(5)}(x - (5)) \\
\therefore y &= \frac{-3}{-9}(x - 5) \\
\therefore y &= \frac{1}{3}x - \frac{5}{3}
\end{align*}
Determine the equation of the perpendicular bisector of \(BD\).
The perpendicular bisector of \(BD\) passes through \(E\) and has a gradient \(-\dfrac{1}{m_{BD}}\)
\begin{align*}
m &= -\frac{1}{m_{BD}} \\
m &= \frac{1}{-\frac{1}{3}} \\
m &= -3 \\ \\
y &= mx + c \\
- \frac{3}{2} &= (3)(\frac{1}{2}) + c \\
c &= - \frac{3}{2} + \frac{3}{2} \\
c &= 0\\
\therefore y &= -3x
\end{align*}
Determine the gradient of \(AC\).
\begin{align*}
m &= \frac{y_2 - y_1}{x_2 - x_1} \\
&= \frac{6 - (-9)}{-3 - 4} \\
m_{AC} &= -\frac{15}{7}
\end{align*}
Is \(ABCD\) a rhombus? Explain why or why not.
\begin{align*}
m_{AC} \times m_{BD} &= -\frac{15}{7} \times \frac{1}{3} \\
&= -\frac{15}{21} \neq -1
\end{align*}
No, \(ABCD\) is not a rhombus because the diagonals do not intersect at right angles.
Find the length of \(AB\).
\begin{align*}
d &= \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \\
AB &= \sqrt{(-3 - 5))^2 + (6 - 0)^2} \\
&= \sqrt{8^2 + 6^2} \\
&= \sqrt{64 + 36} \\
&= \sqrt{100} \\
&= 10
\end{align*}