End of chapter exercises | Algebraic expressions

Textbook Exercise 1.11

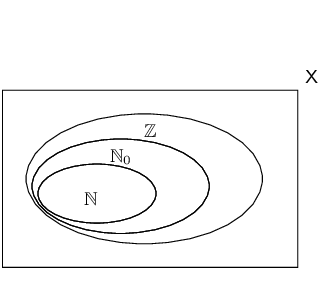
Where does the number \(\text{2,13}\) belong in the diagram?

\(\text{2,13}\) is in its simplest form, therefore it is not in \(\mathbb{N}\), \(\mathbb{N}_0\) or \(\mathbb{Z}\). It is in the space between the rectangle and \(\mathbb{Z}\)

In the following list, there are two false statements and one true statement. Which of the statements is true?

Every natural number is an integer.
Every whole number is a natural number.
There are fractions in the integers.

Consider each statement:

Integers are natural numbers and negative natural numbers. Therefore this statement is true.
\(\text{0}\) is not a natural number, therefore this statement is false.
Integers are natural numbers and negative natural numbers, no fractions. Therefore this is false.

The only true statement is (i).

\(-\sqrt{-5}\)

This is the square root of a negative number and so is non-real.

\(\dfrac{\sqrt{8}}{0}\)

We are dividing by 0 and so this is undefined.

\(-\sqrt{15}\)

This is the square root of a positive number and so is real.

\(-\sqrt{7}\)

This is the square root of a positive number and so is real.

\(\sqrt{-1}\)

This is the square root of a negative number and so is non-real.

\(\sqrt{2}\)

This is the square root of a positive number and so is real.

\(\sqrt[3]{4}\)

Irrational. It cannot be simplified to a fraction of integers.

\(45\pi\)

Irrational. It cannot be simplified to a fraction of integers

\(\sqrt{9}\)

\(\sqrt{9} = 3\)

Rational. Can be simplified to an integer

\(\sqrt[3]{8}\)

\(\sqrt[3]{8} = 2\)

Rational. Can be simplified to an integers.

\(\dfrac{-b}{a}\)

We have a fraction of integers and so this is rational.

\(c \div c\)

When we divide a number by itself we get 1 and so this is rational.

\(\dfrac{a}{c}\)

We are dividing an integer by an irrational number and so this is irrational. However if \(a = 0\) then the fraction is equal to 0 and the number is rational.

\(\dfrac{1}{c}\)

We are dividing an integer by an irrational number and so this is irrational.

Which of the numbers are non-real numbers?

Only \(\sqrt{-24}\) is non-real as it is the square root of a negative number.

Without using a calculator, rank all the real numbers in ascending order.

We exclude \(\sqrt{-24}\) from the list as it is non-real. We also exclude \(\frac{\sqrt{2}}{0}\) as it is undefined. Then we note that:

\(\sqrt[3]{26}\) lies between 2 and 8
\(\frac{3}{2} = \text{1,5}\)
\(\sqrt{39}\) lies between 6 and 7
\(\pi^{2} \approx \text{9,8696}\)
\(\frac{\pi}{2} \approx \text{1,5708}\)
\(-\sqrt{24}\) lies between \(-\text{4}\) and \(-\text{5}\)
\(3\pi \approx \text{9,4248}\)
\(\sqrt{78}\) lies between 8 and 9
\(\pi \approx \text{3,1416}\)

Therefore the ordering is: \(-\sqrt{24} \; ; \; \frac{3}{2} \; ; \; \frac{\pi}{2} \; ; \; \sqrt[3]{26} \; ; \; \pi \; ; \; \sqrt{39} \; ; \; \text{7,}\dot{1}\dot{1} \; ; \; \text{7,12} \; ; \; \sqrt{78} \; ; \; 9 \; ; \; 3\pi \; ; \; \pi^2\)

Which of the numbers are irrational numbers?

Any number that cannot be written as a fraction of integers is irrational. Therefore \(-\sqrt{24} \; ; \; \frac{\pi}{2} \; ; \; \sqrt[3]{26} \; ; \; \pi \; ; \; \sqrt{39} \; ; \; \sqrt{78} \; ; \; 3\pi \; ; \; \pi^2\) are all irrational.

Which of the numbers are rational numbers?

All numbers that can be written as a fraction of integers are rational numbers. Therefore \(\frac{3}{2} \; ; \; \text{7,}\dot{1}\dot{1} \; ; \; \text{7,12} \; ; \; 9\) are all rational numbers.

Which of the numbers are integers?

Only \(9\) is an integer.

Which of the numbers are undefined?

Any fraction that has a denominator of 0 is undefined, therefore only \(\frac{\sqrt{2}}{0}\) is undefined.

\(\text{0,12}\)

\begin{align*} \text{0,12} &= \frac{1}{10} + \frac{2}{100} \\ &= \frac{12}{100} \\ &= \frac{3}{25} \end{align*}

\(\text{0,006}\)

\begin{align*} \text{0,006} &= \frac{6}{\text{1 000}} \\ &= \frac{3}{\text{500}} \end{align*}

\(\text{4,}\overline{\text{14}}\)

\begin{align*} x &= \text{4,141414}\ldots \\ 100x &= \text{414,141414}\ldots \\ 100x - x &= (\text{414,141414}\ldots) - (\text{4,141414}\ldots) \\ \text{99}x &= \text{410} \\ \therefore x &= \frac{\text{410}}{\text{99}} \end{align*}

\(\text{1,59}\)

\begin{align*} \text{1,59} &= 1 + \frac{5}{10} + \frac{9}{100} \\ &= 1\frac{59}{100} \end{align*}

\(\text{12,27}\dot{7}\)

\begin{align*} x & = \text{12,27}\dot{7} \\ 10x &= \text{122,}\dot{7} \\ 100x & = \text{1 227,}\dot{7} \\ \therefore 100x - 10x & = 90x = \text{1 105} \\ \therefore x &= \frac{\text{1 105}}{90} \\ &= \frac{221}{18} \end{align*}

\(\text{0,8}\dot{\text{2}}\)

\begin{align*} \text{0,8} \dot{\text{2}} &= \text{0,8} \text{2 222,..} \\ x &= \text{0,8222...} \\ 10x &= \text{8,222...} \\ 100x &= \text{82,222...} \\ 100x -10x& = \text{82,222} - \text{8,222...} \\ \text{90}x & = \text{74,000} \\ \text{90}x & = \text{74} \\ \therefore x & = \frac{\text{37}}{\text{45}} \end{align*}

\(\text{7,}\overline{\text{36}}\)

\begin{align*} x &= \text{7,363636...} \\ 100x &= \text{736,363636...} \\ 100x - x &= (\text{736,363636...}) - (\text{7,363636...}) \\ \text{99}x &= \text{729} \\ \therefore x &= \frac{\text{81}}{\text{11}} \end{align*}

Show that the decimal \(\text{3,21}\dot{1}\dot{8}\) is a rational number.

\begin{align*} x & = \text{3,21}\dot{1}\dot{8}\\ \text{1 000}x & = \text{32 118,}\overline{18} \\ \therefore \text{10 000}x - x & = \text{9 999}x = \text{32 115} \\ \therefore x & = \frac{\text{32 115}}{\text{9 999}} \end{align*}

This is a rational number because both the numerator and denominator are integers.

\(\dfrac{\text{1}}{\text{18}}\)

\begin{align*} \text{18}|\overline{\text{1,0000}} &= \text{0} \text{ remainder } \text{0} \\ \text{18}|\overline{\text{1,}^1\text{0 000}} &= \text{0} \text{ remainder } \text{0} \\ \text{18}|\overline{\text{1,}^{10}\text{0}^1\text{000}} &= \text{5} \text{ remainder } \text{10} \\ \text{18}|\overline{\text{1,}^{10}\text{0}^1\text{0}^1\text{00}} &= \text{5} \text{ remainder } \text{10} \\ \frac{\text{1}}{\text{18}} &= \text{0,05555...} \\ &= \text{0,0}\dot{\text{5}} \end{align*}

\(1\frac{\text{1}}{\text{2}}\)

\begin{align*} 1\frac{\text{1}}{\text{2}} = \frac{3}{2} \\ \text{2}|\overline{\text{3,0000}} &= \text{1} \text{ remainder } \text{1} \\ \text{2}|\overline{\text{3,}^1\text{0 000}} &= \text{5} \text{ remainder } \text{0} \\ &=\text{1,5} \end{align*}

Express \(\text{0,}\overline{78}\) as a fraction \(\frac{a}{b}\) where \(a, b \in \mathbb{Z}\) (show all working).

\begin{align*} x & = \text{0,}\overline{78} \\ 100x & = \text{78,}\overline{78} \\ \therefore 100x - x & = 99 \\ \therefore x & = \frac{78}{99} \end{align*}

\(\text{1,11235...}\)

The number does not terminate (this is shown by the \(\ldots\)). There is also no indication of a repeating pattern of digits since there is not dot or bar over any of the numbers. The next three digits could be any numbers.
Irrational, there is no repeating pattern.

\(\text{1,}\dot{1}\)

Since there is a dot over the 1 we know that the 1 repeats. The next three digits are: \(111\)
Rational, there is a repeating pattern of digits.

\(\frac{1}{2}\)

To write to two decimal places we must convert to decimal: \(\frac{1}{2}=\text{0,50}\).

\(\text{1}\)

To write to two decimal places just add a comma and two \(\text{0}\)'s: \(\text{1,00}\).

\(\text{0,11111}\bar{1}\)

We mark where the cut off point is, determine if it has to be rounded up or not and then write the answer. In this case there is a \(\text{1}\) after the cut off point so we do not round up. The final answer is: \(\text{0,11111}\overline{1} \approx \text{0,11}\).

\(\text{0,99999}\bar{1}\)

We mark where the cut off point is, determine if it has to be rounded up or not and then write the answer. In this case there is a \(\text{9}\) after the cut off point so we round up. The final answer is: \(\text{0,99999}\overline{1} \approx \text{1,00}\).

\(\text{3,141592654...}\)

\(\text{3,142}\) (round up as there is a \(\text{5}\) after the cut off point).

\(\text{1,618033989...}\)

\(\text{1,618}\) (no rounding as there is a \(\text{0}\) after the cut off point).

\(\text{1,41421356...}\)

\(\text{1,414}\) (no rounding as there is a \(\text{2}\) after the cut off point).

\(\text{2,71828182845904523536...}\)

\(\text{2,718}\) (no rounding as there is a \(\text{2}\) after the cut off point).

Round off the number \(\text{1 523,00195593}\) to \(\text{4}\) decimal places.

\[\text{1 523,00195593} \approx \text{1 523,0020}\]

Round off the number \(\text{1 982,94028996}\) to \(\text{6}\) decimal places.

\[\text{1 982,94028996} \approx \text{1 982,940290}\]

Round off the number \(\text{101,52378984}\) to \(\text{4}\) decimal places.

\[\text{101,52378984} \approx \text{101,5238}\]

\(\sqrt{2}\)

\[\sqrt{2} \approx \text{1,414213562...} \approx \text{1,414}\]

\(\sqrt{3}\)

\[\sqrt{3} \approx \text{1,732050808...} \approx \text{1,732}\]

\(\sqrt{5}\)

\[\sqrt{5} \approx \text{2,236067977...} \approx \text{2,236}\]

\(\sqrt{6}\)

\[\sqrt{6} \approx \text{2,449489743...} \approx \text{2,449}\]

\(\sqrt{8}\)

\[\sqrt{8} \approx \text{2,828427125...} \approx \text{2,82843}\]

Irrational number.

\(\sqrt{768}\)

\[\sqrt{768} \approx \text{27,71281292...} \approx \text{27,71281}\]

Irrational number.

\(\sqrt{\text{0,49}}\)

\[\sqrt{\text{0,49}} = \text{0,70000}\]

Rational number.

\(\sqrt{\text{0,0016}}\)

\[\sqrt{\text{0,0016}} = \text{0,04000}\]

Rational number.

\(\sqrt{\text{0,25}}\)

\[\sqrt{\text{0,25}} = \text{0,50000}\]

Rational number.

\(\sqrt{36}\)

\[\sqrt{36} = \text{6,00000}\]

Rational number.

\(\sqrt{1960}\)

\[\sqrt{1960} \approx \text{44,27188724...} \approx \text{44,27189}\]

Irrational number.

\(\sqrt{\text{0,0036}}\)

\[\sqrt{\text{0,0036}} = \text{0,06000}\]

Rational number.

\(-8\sqrt{\text{0,04}}\)

\[-8\sqrt{\text{0,04}} = -8(\text{0,20000}) = -\text{1,60000}\]

Rational number.

\(5\sqrt{80}\)

\[5\sqrt{80} \approx 5(\text{8,94427191...}) \approx \text{44,72136}\]

Irrational number.

\(\frac{\sqrt{2}}{2}\) to the nearest \(\text{2}\) decimal places.

\begin{align*} \frac{\sqrt{2}}{2} & \approx \text{0,7071...} \\ & \approx \text{0,71} \end{align*}

\(\sqrt{14}\) to the nearest \(\text{3}\) decimal places.

\begin{align*} \sqrt{14} & \approx \text{3,741657...} \\ & \approx \text{3,742} \end{align*}

\(\text{3,141592654...}\)

\begin{align*} \text{3,141592654...} & \approx \text{3,142} \\ & \approx 3 \frac{142}{\text{1 000}} \\ & \approx \frac{\text{1 571}}{\text{500}} \end{align*}

\(\text{1,618033989...}\)

\begin{align*} \text{1,618033989...} & \approx \text{1,618} \\ & \approx 1 \frac{618}{\text{1 000}} \\ & \approx \frac{\text{809}}{\text{500}} \end{align*}

\(\text{1,41421356...}\)

\begin{align*} \text{1,41421356...} & \approx \text{1,414} \\ & \approx 1 \frac{414}{\text{1 000}} \\ & \approx \frac{\text{707}}{\text{500}} \end{align*}

\(\text{2,71828182845904523536...}\)

\begin{align*} \text{2,71828182845904523536...} & \approx \text{2,718} \\ & \approx 2 \frac{718}{\text{1 000}} \\ & \approx \frac{\text{1 359}}{\text{500}} \end{align*}

\(\sqrt{5}\)

\[2 \text{ and } 3 ~(2^2 = 4 \text{ and } 3^2=9)\]

\(\sqrt{10}\)

\[3 \text{ and } 4 ~(3^2 = 9 \text{ and } 4^2=16)\]

\(\sqrt{20}\)

\[4 \text{ and } 5 ~(4^2 = 16 \text{ and } 5^2 = 25)\]

\(\sqrt{30}\)

\[5 \text{ and } 6 ~(5^2 = 25 \text{ and } 6^2 = 36)\]

\(\sqrt[3]{5}\)

\[1 \text{ and } 2 ~(1^3 = 1 \text{ and } 2^3=8)\]

\(\sqrt[3]{10}\)

\[2 \text{ and } 3 ~(2^3 = 8 \text{ and } 3^3 = 27)\]

\(\sqrt[3]{20}\)

\[2 \text{ and } 3 ~(2^3 = 8 \text{ and } 3^3=27)\]

\(\sqrt[3]{30}\)

\[3 \text{ and } 4 ~(3^3 = 27 \text{ and } 4^3 = 64)\]

\(\sqrt{90}\)

\[9 \text{ and } 10 ~(9^2 = 81 \text{ and } 10^2 = 100)\]

\(\sqrt{72}\)

\[8 \text{ and } 9 ~(8^2 = 64 \text{ and } 9^2 = 81)\]

\(\sqrt[3]{58}\)

\[3 \text{ and } 4 ~(3^3 = 27 \text{ and } 4^3 = 64)\]

\(\sqrt[3]{118}\)

\[4 \text{ and } 5 ~(4^3 = 64 \text{ and } 5^3 = 125)\]

\(\sqrt{14}\)

\(\sqrt{14}\) lies between 3 and 4. Since \(3^{2} = 9\) and \(4^{2} = 16\) it lies closer to 4 than to 3.

Therefore \(\text{3,7}\) or \(\text{3,8}\) are suitable estimates.

\(\sqrt{110}\)

\(\sqrt{110}\) lies between 10 and 11. Since \(10^{2} = 100\) and \(11^{2} = 121\) it lies almost exactly between 10 and 11.

Therefore \(\text{10,5}\) is a suitable estimate.

\(\sqrt{48}\)

\(\sqrt{48}\) lies between 6 and 7. Since \(6^{2} = 36\) and \(7^{2} = 49\) it lies closer to 7 than to 6.

Therefore \(\text{6,9}\) is a suitable estimate.

\(\sqrt{57}\)

\(\sqrt{57}\) lies between 7 and 8. Since \(7^{2} = 49\) and \(8^{2} = 64\) it lies almost exactly between the two numbers.

Therefore \(\text{4,5}\) or \(\text{4,6}\) are suitable estimates.

\((a + 5)^2\)

\begin{align*} (a + 5)^2 & = (a + 5)(a + 5) \\ &= a^2 + 5a + 5a + 25\\ &=a^2 + 10a + 25 \end{align*}

\((n + 12)^2\)

\begin{align*} (n + 12)^2 & = (n + 12)(n + 12) \\ &= n^2 + 12n + 12n + 144 \\ &=n^2 + 24n +144 \end{align*}

\((d - 4)^2\)

\begin{align*} (d - 4)^2 & = (d - 4)(d - 4) \\ &= d^2 - 4d - 4d + 16\\ &=d^2 - 8d + 16 \end{align*}

\((7w + 2)(7w - 2)\)

\begin{align*} (7w + 2)(7w - 2) &= 49w^{2} - 14w + 14w - 4\\ &= 49 w^{2} - 4 \end{align*}

\((12 q + 1)(12 q - 1)\)

\begin{align*} (12 q + 1)(12 q - 1) &= 144 q^{2} - 12q + 12q -1\\ &= 144 q^{2} - 1 \end{align*}

\(-(-x - 2)(x + 2)\)

\begin{align*} -(-x - 2)(x + 2) &=(x + 2)(x + 2) \\ & = x^{2} + 2x + 2x + 4\\ & = x^{2} + 4x + 4 \end{align*}

\((5 k - 4)(5 k + 4)\)

\begin{align*} (5 k - 4)(5 k + 4) &= 25 k^{2} + \text{20} k - \text{20} k -16\\ &= 25 k^{2} - 16 \end{align*}

\((5 f + 4)(2 f + 2)\)

\begin{align*} (5 f + 4)(2 f + 2) &= 10 f^{2} + 10 f + 8 f + 8\\ &= 10 f^{2} + 18 f + 8 \end{align*}

\((3 n + 6)(6 n + 5)\)

\begin{align*} (3 n + 6)(6 n + 5) &= 18 n^{2} + 15 n + 36 n + 30 \\ &= 18 n^{2} + 51 n + 30 \end{align*}

\((2 g + 6)(g + 6)\)

\begin{align*} (2 g + 6)(g + 6) &= 2 g^{2} + 12 g + 6 g + 36 \\ &= 2 g^{2} + 18 g + 36 \end{align*}

\((4 y + 1)(4 y + 8)\)

\begin{align*} (4 y + 1)(4 y + 8) &= 16 y^{2} + 32 y + 4y +8 \\ &= 16 y^{2} + 36 y + 8 \end{align*}

\((d - 3)(7 d + 2)\)

\begin{align*} (d - 3)(7 d + 2) &= 7 d^{2} + 2d - 21d - 6 \\ &= 7 d^{2} - 19 d - 6 \end{align*}

\((6 z - 4)(z - 2)\)

\begin{align*} (6 z - 4)(z - 2) &= 6 z^{2} - 12 z - 4 z + 8 \\ &= 6 z^{2} - 16 z + 8 \end{align*}

\((5w - 11)^2\)

\begin{align*} (5w - 11)^2 & = (5w - 11)(5w - 11) \\ & = 25w^{2} - 55w - 55w + 121 \\ &= 25w^{2} - 110w + 121 \end{align*}

\((5s - 1)^2\)

\begin{align*} (5s - 1)^2 & = (5s - 1)(5s - 1) \\ & = 25s^{2} - 5s - 5s + 1 \\ &= 25 s^{2} - 10s + 1 \end{align*}

\((3d -8)^2\)

\begin{align*} (3d - 8)^2 & = (3d - 8)(3d - 8) \\ & = 9d^2 - 24d - 24d + 64 \\ &= 9d^2 - 48d + 64 \end{align*}

\(5f^2(3f + 5) + 7f(3f^2 + 7)\)

\begin{align*} 5f^2(3f + 5) + 7f(3f^2 + 7) &= 15f^3 + 25f^2 + 21f^3 + 49f \\ &= 36f^3 + 25f^2 + 49f \end{align*}

\(8d(4d^3 + 2) + 6d^2(7d^2 + 4)\)

\begin{align*} 8d(4d^3 + 2) + 6d^2(7d^2 + 4) &=32d^4 + 16d + 42d^4 + 24d^2\\ &= 74d^4 + 16d + 24d^2 \end{align*}

\(\text{5}{x}^2(\text{2}{x}+\text{2}) + \text{7}{x}(\text{7}{x}^2 + \text{7})\)

\begin{align*} \text{5}{x}^2(\text{2}{x} + \text{2}) + \text{7}{x}(\text{7}{x}^2 + \text{7}) &= \text{10}{x}^3 + \text{10}{x}^2 + \text{49}{x}^3 + \text{49}{x}\\ &= \text{59}{x}^3 + \text{10}{x}^2 + \text{49}{x} \end{align*}

\((y^4 + 3y^2 + y)(y+1)(y-2)\)

\begin{align*} (y^4 + 3y^2 + y)(y+1)(y-2) &= (y^4 + 3y^2 + y)(y^2 - y - 2) \\ & = y^6 - y^5 - 2y^4 + 3y^4 - 3y^3 - 6y^2 + y^3 - y^2 -2y \\ & = y^6 - y^5 + y^4 - 2y^3 - 7y^2 - 2y \end{align*}

\((x+1)^2 - (x-1)^2\)

\begin{align*} (x+1)^2 - (x-1)^2 &= x^2 + 2x + 1 - (x^2 -2x + 1) \\ &= x^2 + 2x + 1 - x^2 + 2x - 1 \\ &= 4x \end{align*}

\((x^2 + 2x + 1)(x^2 -2x + 1)\)

\begin{align*} (x^2 + 2x + 1)(x^2 -2x + 1) &= x^4 - 2x^3 + x^2 + 2x^3 - 4x^2 + 2x + x^2 - 2x + 1 \\ &=x^4 - 2x^2 + 1 \end{align*}

\((4a - 3b)(16a^2 + 12ab + 9b^2)\)

\begin{align*} (4a - 3b)(16a^2 + 12ab + 9b^2) &= 64a^3 + 48a^2b + 36ab^2 - 48a^2b - 36ab^2 - 27b^3 \\ &=64a^3 - 27b^3 \end{align*}

\(2(x + 3y)(x^2 - xy - y^2)\)

\begin{align*} 2(x + 3y)(x^2 - xy - y^2) &= 2(x^3 - x^2y - xy^2 + 3x^2y - 3xy^2 - 3y^3) \\ &=2x^3 + 4x^2y - 8xy^2 - 6y^3 \end{align*}

\((3a - 5b)(3a + 5b)(a^2 + ab - b^2)\)

\begin{align*} (3a - 5b)(3a + 5b)(a^2 + ab - b^2) &= (9a^2 - 25b^2)(a^{2} + ab - b^2) \\ & = 9a^4 + 9a^3 - 9a^2b^2 - 25a^2b^2 + 25ab^3 - 25b^4 \\ & = 9a^4 + 9a^3 - 34a^2b^2 + 25ab^3 - 25b^4 \end{align*}

\(\left(y - \dfrac{1}{y}\right)\left(y + \dfrac{1}{y}\right)\)

\begin{align*} \left(y - \frac{1}{y}\right)\left(y + \frac{1}{y}\right) &= y^2 + 1 -1 + \frac{1}{y^2} \\ &= y^2 - \frac{1}{y^2} \end{align*}

\(\left(\dfrac{a}{3} - \dfrac{3}{a}\right)\left(\dfrac{a}{3} + \dfrac{3}{a}\right)\)

\begin{align*} \left(\frac{a}{3} - \frac{3}{a}\right)\left(\frac{a}{3} + \frac{3}{a}\right) &= \frac{a^2}{9} + 1 - 1+ \frac{3}{a^2} \\ &= \frac{a^2}{9} - \frac{3}{a^2} \end{align*}

\(\dfrac{1}{3}(12x - 9y) + \dfrac{1}{6}(12x + 18y)\)

\begin{align*} \frac{1}{3}(12x - 9y) + \frac{1}{6}(12x + 18y) &= 4x - 3y + 2x + 3y \\ &=6x \end{align*}

\((x+2)(x-2) - (x+2)^2\)

\begin{align*} (x+2)(x-2) - (x+2)^2 &= x^2 - 4 - (x^2 + 4x + 4) \\ &= -4x - 8 \end{align*}

What is the value of \(e\) in \((x - 4)(x + e) = x^2 - 16\)?

\[(x - 4)(x + e) = x^{2} + ex - 4x - 4e\]

From the constant term we see that \(4e = 16\), therefore \(e = 4\).

For which of these values of \(k\) will \(b\) be positive?

\(-6 \; ; \; -1 \; ; \; 0 \; ; \; 1 \; ; \; 6\)

\begin{align*} (x + 2)(x + k) & = x^2 + kx + 2x + 2k \\ & = x^2 + (k + 2)x + 2k \end{align*}

The \(b\) term is \(k + 2\) and so any value greater than \(-\text{2}\) will make the \(b\) term positive.

Therefore \(-1 \; ; \; 0 \; ; \; 1 \; ; \; 6\)

For which of these values of \(k\) will \(c\) be positive?

\(-6 \; ; \; -1 \; ; \; 0 \; ; \; 1 \; ; \; 6\)

From above we see that the \(c\) term is \(2k\). Therefore any positive value of \(k\) will make \(c\) positive.

Therefore \(0 \; ; \; 1 \; ; \; 6\)

For what values of \(k\) will \(c\) be positive?

From above we see that the \(c\) term is \(2k\). Therefore any positive value of \(k\) will make \(c\) positive.

Therefore \(k > 0\)

For what values of \(k\) will \(b\) be positive?

From above we see that any value greater than \(-\text{2}\) will make the \(b\) term positive.

Therefore \(k > -2\).

Expand: \(\left(3a - \dfrac{1}{2a}\right)^2\)

\begin{align*} \left(3a - \frac{1}{2a}\right)^2 &= 9a^2 + 3 + \frac{1}{4a^2} \end{align*}

Expand: \(\left(3a - \dfrac{1}{2a}\right)\left(9a^2 + \dfrac{3}{2} + \dfrac{1}{4a^2}\right)\)

\begin{align*} \left(3a - \frac{1}{2a}\right)\left(9a^2 + \frac{3}{2} + \frac{1}{4a^2}\right) &= 27a^3 + \frac{9}{2}a + \frac{3}{4a} - \frac{9}{2}a - \frac{3}{4a} - \frac{1}{8a^3} \\ &=27a^3 - \frac{1}{8a^3} \end{align*}

Given that \(3a - \dfrac{1}{2a} = 7\), determine the value of \(27a^3 - \dfrac{1}{8a^3}\) without solving for \(a\).

\begin{align*} 27a^3 - \frac{1}{8a^3} &= \left(3a - \frac{1}{2a}\right)\left(9a^2 + \frac{3}{2} + \frac{1}{4a^2}\right) \\ &= 7\left(9a^2 + \frac{3}{2} + \frac{1}{4a^2}\right) \\ \\ 9a^2 + \frac{3}{2} + \frac{1}{4a^2} &= \left(3a - \frac{1}{2a}\right)^2 + \frac{9}{2} \\ &= 7^2 + \frac{9}{2} \\ \\ 27a^3 - \frac{1}{8a^3} &= 374\frac{1}{2} \end{align*}

\(17^2 - 15^2\)

\begin{align*} 17^2 - 15^2 &= (17-15)(17+15) \\ &=2(32) \\ &=64 \end{align*}

\(13^2 -12^2\)

\begin{align*} 13^2 -12^2 &= (13-12)(13+12) \\ &= 25 \end{align*}

\(120045^2 - 120035^2\)

\begin{align*} 120045^2 - 120035^2 &= (120045 - 120035)(120045 + 120035) \\ &= 10(240080) \\ &= 2400800 \end{align*}

\(26^2 - 24^2\)

\begin{align*} 26^2 - 24^2 &= (26-24)(26+24) \\ &=2(50) \\ &= 100 \end{align*}

\(143\)

\begin{align*} 143 &= 144- 1 \\ &=(12-1)(12+1) \\ &=11 \times 13 \end{align*}

\(168\)

\begin{align*} 168 &= 169 - 1 \\ &=(13-1)(13+1) \\ &=12(14) \\ &=3 \times 2^2 \times 2 \times 7 \\ &=2^3 \times 3 \times 7 \end{align*}

\(899\)

\begin{align*} 899 &= 900 - 1 \\ &=(30- 1)(30+1) \\ &=29 \times 31 \end{align*}

\(99\)

\begin{align*} 99 &= 100 - 1 \\ &=(10-1)(10+1) \\ &=3^2 \times 11 \end{align*}

\(1599\)

\begin{align*} 1599 &= 1600 -1 \\ &=(40-1)(40+1) \\ &=39(41)\\ &=3 \times 13 \times 41 \end{align*}

\(a^{2} - 9\)

\[{a}^{2} - 9 = (a - 3)(a + 3)\]

\(9b^{2} - 81\)

\begin{align*} 9b^{2} - 81 & = 9(b^{2} - 9)\\ & = 9(b - 3)(b + 3) \end{align*}

\(m^{2} - \frac{1}{9}\)

\[m^{2} - \frac{1}{9} = \left(m - \frac{1}{3}\right)\left(m + \frac{1}{3}\right)\]

\(5 - 5a^{2}b^{6}\)

\begin{align*} 5 - 5a^{2}b^{6} & = 5(1 - a^{2}b^{6})\\ & = 5(1 - ab^{3})(1 + ab^{3}) \end{align*}

\(16ba^{4} - 81b\)

\begin{align*} 16ba^{4} - 81b & = b(16a^{4} - 81)\\ & = b(4a^{2} - 9)(4a^{2} + 9) \\ & = b(2a - 3)(2a + 3)(4a^{2} + 9) \end{align*}

\(a^{2} - 10a + 25\)

\[a^{2} - 10a + 25 = (a - 5)(a - 5)\]

\(16b^{2} + 56b + 49\)

\[16b^{2} + 56b + 49 = (4b + 7)(4b + 7)\]

\(-4b^{2} - 144b^{8} + 48b^{5}\)

\begin{align*} -4b^{2} - 144b^{8} + 48b^{5} & = -4b^{2}(1 + 36b^{6} - 12b^{3}) \\ & = -4b^{2}(6b^{3} - 1)(6b^{3} - 1)\\ & = -4b^{2}(6b^{3} - 1)^{2} \end{align*}

\(16 - x^{4}\)

\begin{align*} 16 - x^{4} & = (4 - x^{2})(4 + x^{2}) \\ & = (4 + x^{2})(2 + x)(2 - x) \end{align*}

\(7x^{2} - 14x + 7xy - 14y\)

\begin{align*} 7x^{2} - 14x + 7xy - 14y & = 7(x^{2} - 2x + xy - 2y)\\ & = 7(x(x - 2) + y(x - 2)) \\ & = 7(x - 2)(x + y) \end{align*}

\(y^{2} - 7y - 30\)

\[y^{2} - 7y - 30 = (y - 10)(y + 3)\]

\(1 - x - x^{2} + x^{3}\)

\begin{align*} 1 - x - x^{2} + x^{3} & = (1 - x) - x^{2}(1 - x)\\ & = (1 - x)(1 - x^{2}) \\ & = (1 - x)(1 - x)(1 + x) \\ & = (1 - x)^{2}(1 + x) \end{align*}

\(-3(1 - p^{2}) + p + 1\)

\begin{align*} -3(1 - p^{2}) + p + 1 & = -3(1 - p)(1 + p) + (1 + p)\\ & = (1 + p)[-3(1 - p) + 1] \\ & = (1 + p)(-2 + 3p) \end{align*}

\(x^{2} - 2x + 1 - y^{4}\)

\begin{align*} x^{2} - 2x + 1 - y^{4} & = x(x - 2) + (1 - y^2)(1 + y^2)\\ &= x(x - 2) + (1 + y)(1 - y)(1 + y^2) \end{align*}

\(4b(x^{3} - 1) + x(1 - x^{3})\)

\begin{align*} 4b(x^{3} - 1) + x(1 - x^{3}) & = (x^3 - 1)(4b - x)\\ &= (x - 1)(x^2 + x + 1)(4b - x) \end{align*}

\(3m(v-7)+19(-7 + v)\)

\begin{align*} 3 m (v-7) +19 (-7 + v) & = 3 m (v-7) +19 (v-7) \\ & = (v-7)(3m+19) \end{align*}

\(3f(z+3)+19(3 + z)\)

\begin{align*} 3 f (z+3) +19 (3 + z) & = 3 f (z+3) +19 (z+3) \\ &= (3f+19)(z+3) \end{align*}

\(3p^{3} - \frac{1}{9}\)

\[3p^{3} - \frac{1}{9} = 3(p - \frac{1}{3})(p^2 + \frac{p}{3} + \frac{1}{9})\]

\(8x^{6} - 125y^{9}\)

\[8x^{6} - 125y^{9} = (2x^2 - 5y^3)(4x^4 + 10x^2y^3 + 25y^6)\]

\((2 + p)^{3} - 8(p + 1)^{3}\)

\begin{align*} (2 + p)^{3} - 8(p + 1)^{3} & = [(p + 2) - 2(p + 1)][(p + 2)^2 + 2(p + 2)(p + 1) + 4(p + 1)^2] \\ & = [p + 2 - 2p - 2][p^2 + 4p + 4 + 2p^2 + 6p + 4 + 4p^2 + 8p + 4] \\ & = (-p)(12 + 18p + 7p^2) \end{align*}

\(\dfrac{1}{3}a^3 - a^2b + 2a^2b - 6ab^2 +3ab^2 - 9b^3\)

\begin{align*} \frac{1}{3}a^3 - a^2b + 2a^2b - 6ab^2 +3ab^2 - 9b^3 &= \frac{1}{3}a^{2}(a - 3b) + 2ab(a -3b) + 3b^2(a -3b) \\ &=(\frac{1}{3}a^{2} + 2ab + 3b^2)(a-3b) \\ &=\frac{(a^2+ 6ab + 9b^2)(a -3b)}{3} \\ &=\frac{(a + 3b)^2(a -3b)}{3} \end{align*}

\(6a^{2}-17a+5\)

\[6a^{2}-17a+5 = (2a-5)(3a-1)\]

\(s^{2}+2s-15\)

\[s^{2}+2s-15 = (s-3)(s+5)\]

\(16v +24h +2j^{5}v +3j^{5}h\)

\begin{align*} 16v +24h +2j^{5}v +3j^{5}h &= 8 (2v +3h) +j^{5} (2v +3h) \\ &= (2v +3h) (8 +j^{5}) \end{align*}

\(18h -45g +2m^{3}h -5m^{3}g\)

\begin{align*} 18h -45g +2m^{3}h -5m^{3}g &= 9 (2h -5g) +m^{3} (2h -5g) \\ &= (2h -5g) (9 +m^{3}) \end{align*}

\(63d -18s +7u^{2}d -2u^{2}s\)

\begin{align*} 63d -18s +7u^{2}d -2u^{2}s &= 9 (7d -2s) +u^{2} (7d -2s) \\ &= (7d -2s) (9 +u^{2}) \end{align*}

\(6 a^{2} + 14 a + 8\)

\begin{align*} 6 a^{2} + 14 a + 8 & = \text{2} (3 a^{2} + 7 a + 4)\\ & = \text{2} \left(a + 1 \right) \left( 3 a + 4 \right) \end{align*}

\(6 g^{2} - 15 g - 9\)

\begin{align*} 6 g^{2} - 15 g - 9 & = \text{3} (2 g^{2} - 5 g - 3)\\ & = \text{3} \left(g - 3 \right) \left( 2 g + 1 \right) \end{align*}

\(125g^3 - r^3\)

\[125g^3 - r^3 = (5g -r)(25g^2 +5gr + r^2)\]

\(8r^3 + z^3\)

\[8r^3 + z^3 = (2r +z)(4r^2 -2rz + z^2)\]

\(14m-4n+7jm-2jn\)

\begin{align*} 14m-4n+7jm-2jn &= 2(7m-2n)+j(7m-2n)\\ &= (7m-2n)(2+j) \end{align*}

\(25d-15m+5yd-3ym\)

\begin{align*} 25d-15m+5yd-3ym &= 5(5d-3m)+y(5d-3m)\\ &= (5d-3m)(5+y) \end{align*}

\(g^\text{3}-\text{27}\)

\[g^\text{3}-\text{27} = (g-\text{3})(g^\text{2}\text{+3}g+9)\]

\(z^\text{3}\text{+125}\)

\[z^\text{3}\text{+125} = (z\text{+5})(z^\text{2}-\text{5}z+25)\]

\(b^2 - (3a - 2b)^2\)

\begin{align*} b^2 - (3a - 2b)^2 &= (b - (3a - 2b))(b + 3a - 2b) \\ &= (3b - 3a)(3a -b) \\ &= 3(b-a)(3a - b) \end{align*}

\(9y^2 - (4x + 2y)^2\)

\begin{align*} 9y^2 - (4x + 2y)^2 &= (3y + 4x + 2y)(3y - (4x + 2y)) \\ &=(4x + 5y)(y - 4x) \end{align*}

\(16x^6 - 3y^8\)

\begin{align*} 16x^6 - 3y^8 &= 4(4x^6 - 9y^8) \\ &=4(4x^6 - 9y^8) \\ &=4(4x^3 - 3y^4)(4x^3 + 3y^4) \end{align*}

\(\dfrac{1}{6}a^2 - 24b^4\)

\begin{align*} \frac{1}{6}a^2 - 24b^4 &= \frac{1}{6}\left(a^2 - 144b^4\right) \\ &= \frac{1}{6}\left(a - 12b^2\right)\left(a + 12b^2\right) \end{align*}

\(4(a - 3) - 81x^2(a - 3)\)

\begin{align*} 4(a - 3) - 81x^2(a - 3) &= (a-3)(4- 81x^2)\\ &=(a-3)(2-9x)(2+9x) \end{align*}

\((2+b)^2 - 11(2+b) - 12\)

\begin{align*} (2+b)^2 - 11(2+b) - 12 &= ((2+b) + 1)((2+b) - 12) \\ & = (b+3)(b-10) \end{align*}

\(2x^2 + 7xy + 5y^2\)

\[2x^2 + 7xy + 5y^2 = (2x +5y)(x +y)\]

\(x^2 - 2xy - 15y^2\)

\[x^2 - 2xy - 15y^2 = (x-5y)(x + 3y)\]

\(4x^4 + 11x^2 + 6\)

\[4x^4 + 11x^2 + 6 = (4x^2 + 3)(x^2 + 2)\]

\(6x^4 - 38x^2 + 40\)

\begin{align*} 6x^4 - 38x^2 + 40 &= 2(3x^4 - 19x^2 + 20) \\ &=2(3x^2 - 4)(x^2 - 5) \end{align*}

\(9a^2x + 9a^{2}y + 27a^2 - b^2x - b^2y - 3b^2\)

\begin{align*} 9a^2x + 9a^{2}y + 27a^2 - b^2x - b^2y - 3b^2 &= (9a^2 - b^2)(x + y + 3) \\ &= (3a+ b)(3a -b)(x +y +3) \end{align*}

\(2(2y^2 - 5y) - 24\)

\begin{align*} 2(2y^2 - 5y) - 24 &= 2(2y^2 - 5y) - 2(12) \\ &=2(2y^2 - 5y - 12) \\ &=2(2y + 3)(y-4) \end{align*}

\(\dfrac{1}{2}x^3 - \frac{9}{2}x - 2x^2 + 18\)

\begin{align*} \frac{1}{2}x^3 - \frac{9}{2}x - 2x^2 + 18 &= \frac{x^3 - 9x - 4x^2 +36}{2} \\ &=\frac{x^2(x-4) - 9(x - 4)}{2} \\ &=\frac{(x-4)(x^2 - 9)}{2} \\ &=\frac{(x-4)(x - 3)(x + 3)}{2} \end{align*}

\(27r^3s^3 - 1\)

\[27r^3s^3 - 1 = (3rs -1)(9r^2s^2 +3rs + 1)\]

\(\dfrac{1}{125h^3} + r^3\)

\[\frac{1}{125h^3} + r^3 = \left(\frac{1}{5h} +r\right)\left(\frac{1}{25h^2} -\frac{r}{5h} + r^2\right)\]

\(j(64n^3 - b^3) + k(64n^3 - b^3)\)

\begin{align*} j(64n^3 - b^3) + k(64n^3 - b^3) &= (j+k)(64n^3 - b^3) \\ &= (j + k)(4n - b)(16n^2 +4nb + b^2) \end{align*}

\((a - 2)^{2} - a(a + 4)\)

\begin{align*} (a - 2)^{2} - a(a + 4) & = a^{2} - 4a + 4 - a^{2} - 4a\\ &= -8a + 4 \end{align*}

\((5a - 4b)(25a^{2} + 20ab + 16b^{2})\)

\begin{align*} (5a - 4b)(25{a}^{2} + 20ab + 16{b}^{2}) & = 125a^{3} + 100a^{2}b + 80ab^{2} - 100a^{2}b - 80ab^{2} - 64b^{3}\\ & = 125a^3 - 64b^3 \end{align*}

\((2m - 3)(4m^{2} + 9)(2m + 3)\)

\begin{align*} (2m - 3)(4m^{2} + 9)(2m + 3) & = (4m^{2} - 9)(4m^{2} + 9)\\ & = 16m^{4} - 81 \end{align*}

\((a + 2b - c)(a + 2b + c)\)

\begin{align*} (a + 2b - c)(a + 2b + c) & = a^{2} + 2ab + ac + 2ab + 4b^{2} + 2bc - ac - 2bc - c^{2}\\ & = a^{2} + 4ab + 4b^{2} - c^{2} \end{align*}

\(\dfrac{m^2+11m+18}{4(m^2-4)} \div \dfrac{3m^2+27m}{24m^2-48m}\)

\begin{align*} \frac{m^2+11m+18}{4(m^2-4)} \div \frac{3m^2+27m}{24m^2-48m} &= \frac{m^2+11m+18}{4(m^2-4)} \times \frac{24m^2-48m}{3m^2+27m}\\ &= \frac{(m+9)(m+2)}{4(m-2)(m+2)} \times \frac{24m(m-2)}{3m(m+9)}\\ &= \frac{1}{4} \times \frac{24}{3}\\ &= 2 \end{align*}

\(\dfrac{t^2+9t+18}{5(t^2-9)} \div \dfrac{4t^2+24t}{100t^2-300t}\)

\begin{align*} \frac{t^2+9t+18}{5(t^2-9)} \div \frac{4t^2+24t}{100t^2-300t} &= \frac{t^2+9t+18}{5(t^2-9)} \times \frac{100t^2-300t}{4t^2+24t}\\ &= \frac{(t+6)(t+3)}{5(t-3)(t+3)} \times \frac{100t(t-3)}{4t(t+6)}\\ &= \frac{1}{5} \times \frac{100}{4}\\ &= 5 \end{align*}

\(\dfrac{4 - b^2}{3b - 6}\)

\begin{align*} \frac{4 - b^2}{3b - 6} &= \frac{(2-b)(2+b)}{3(b-2)} \\ &= -\frac{2+b}{3} \end{align*}

\(\dfrac{x^2 + 2x + 4}{x^3 - 8}\)

\begin{align*} \frac{x^2 + 2x + 4}{x^3 - 8} &= \frac{x^2 + 2x + 4}{(x-2)(x^2 + 2x + 4)} \\ &= \frac{1}{x-2} \end{align*}

\(\dfrac{x^2 - 5x - 14}{3x +6}\)

\begin{align*}\frac{x^2- 5x - 14}{3x +6} &= \frac{(x-7)(x+2)}{3(x+2)} \\ &= \frac{x-7}{3} \end{align*}

\(\dfrac{d^2+23d+132}{5(d^2-121)} \div \dfrac{4d^2+48d}{100d^2-1100d}\)

\begin{align*} \frac{d^2+23d+132}{5(d^2-121)} \div \frac{4d^2+48d}{100d^2-1100d} &= \frac{d^2+23d+132}{5(d^2-121)} \times \frac{100d^2-1100d}{4d^2+48d}\\ &= \frac{(d+12)(d+11)}{5(d-11)(d+11)} \times \frac{100d(d-11)}{4d(d+12)}\\ &= \frac{1}{5} \times \frac{100}{4}\\ &= 5 \end{align*}

\(\dfrac{a-2}{a^2 + 4a + 3} \div \dfrac{(a-1)(a+1)}{a-1} \times \dfrac{a^2 - 2a - 15}{a-2}\)

\begin{align*} & \frac{a-2}{a^2 + 4a + 3} \div \frac{(a-1)(a+1)}{a-1} \times \frac{a^2 - 2a - 15}{a-2}\\ &= \frac{a-2}{(a+1)(a+3)} \div \frac{(a-1)(a+1)}{a-1} \times \frac{(a+3)(a-5)}{a-2} \\ &=\frac{a-2}{(a+1)(a+3)} \times \frac{a-1}{(a-1)(a+1)} \times \frac{(a+3)(a-5)}{a-2} \\ &= \frac{a-5}{(a + 2)^{2}} \end{align*}

\(\dfrac{a+6}{a^2 + 12a + 11} \times \dfrac{a^2 + 14a + 33}{a+3} \div \dfrac{a^3 +216}{a+1}\)

\begin{align*} & \frac{a+6}{a^2 + 12a + 11} \times \frac{a^2 + 14a + 33}{a+3} \div \frac{a^3 +216}{a+1} \\ &= \frac{a+6}{(a+11)(a+1)} \times \frac{(a+11)(a+3)}{a+3} \times \frac{a+1}{(a+6)(a^2 + 6a + 36)} \\ &= \frac{1}{a^2 + 6a + 36} \end{align*}

\(2 \div \dfrac{a + b}{a + 2b} \times \dfrac{b^2 - ba -6a^2}{a^2 - 4b^2} \times \dfrac{a^2 - b - 2b^2}{3a -b}\)

\begin{align*} & 2 \div \frac{a + b}{a + 2b} \times \frac{b^2 - ba -6a^2}{a^2 - 4b^2} \times \frac{a^2 - b - 2b^2}{3a -b} \\ & = 2 \times \frac{a + 2b}{a+b} \times \frac{(b-3a)(b +2a)}{(a-2b)(a+2b)} \times \frac{(a-2b)(a+b)}{3a -b} \\ &= -2 (2a + b) \end{align*}

\(\dfrac{st+sb+ 31t+31b}{t+b}\)

\begin{align*} \frac{st+sb + 31t+31b} {(t+b)} &= \frac{s(t+b)+ 31(t+b)}{(t+b)}\\ &= \frac{(t+b)(s+31)}{(t+b)}\\ &= s+31 \end{align*}

\(\dfrac{ny+nq + 8y+8q}{y+q}\)

\begin{align*} \frac{ny+nq + 8y+8q}{(y+q)} &= \frac{n(y+q)+ 8(y+q)}{(y+q)}\\ &= \frac{(y+q)(n+8)}{(y+q)}\\ &= n+8 \end{align*}

\(\dfrac{p^{2} - q^{2}}{p} \div \dfrac{p + q}{p^{2} - pq}\)

\begin{align*} \frac{{p}^{2} - {q}^{2}}{p} \div \frac{p + q}{{p}^{2} - pq} & = \frac{(p - q)(p + q)}{p} \times \frac{p(p - q)}{p + q}\\ & = (p - q)^2\\ & = p^2 - 2pq +q^2 \end{align*}

\(\dfrac{2}{x} + \dfrac{x}{2} - \dfrac{2x}{3}\)

\begin{align*} \frac{2}{x} + \frac{x}{2} - \frac{2x}{3} & = \frac{12 + 3x^2 - 4x^2}{6x}\\ & = \frac{12 - x^2}{6x} \end{align*}

\(\dfrac{1}{a + 7} - \dfrac{a + 7}{a^{2} - 49}\)

\begin{align*} \frac{1}{a + 7} - \frac{a + 7}{a^2 - 49} &= \frac{1}{a + 7} - \frac{a + 7}{(a + 7)(a - 7)}\\ &= \frac{-14}{(a + 7)(a - 7)} \end{align*}

\(\dfrac{x + 2}{2x^{3}} + 16\)

\begin{align*} \frac{x + 2}{2x^3} + 16 &= \frac{(x + 2) + 16(2x^3)}{2x^3}\\ &= \frac{32x^3 + x + 2}{2x^3} \end{align*}

\(\dfrac{1 - 2a}{4a^{2} - 1} - \dfrac{a - 1}{2a^{2} - 3a + 1} - \dfrac{1}{1 - a}\)

\begin{align*} \frac{1 - 2a}{4a^{2} - 1} - \frac{a - 1}{2a^{2} - 3a + 1} - \frac{1}{1 - a} & = \frac{1 - 2a}{(2a - 1)(2a + 1)} - \frac{a - 1}{(2a - 1)(a - 1)} + \frac{1}{a - 1}\\ & = -\frac{(2a - 1)}{(2a - 1)(2a + 1)} - \frac{1}{2a - 1} + \frac{1}{a - 1}\\ &=\frac{4a - 1}{(2a + 1)(2a - 1)(a - 1)} \end{align*}

\(\dfrac{1}{2}x + \dfrac{x-2}{3} + 4\)

\begin{align*} \frac{1}{2}x + \frac{x-2}{3} + 4 &= \frac{3x + 2(x-2) + (2)(3)(4)}{6} \\ &= \frac{3x + 2x - 4 + 24}{6} \\ &= \frac{5x + 20}{6} \end{align*}

\(\dfrac{1}{x^2 + 2x} + \dfrac{4x^2 - x - 3}{x^2 + 2x - 3}\)

\begin{align*} \frac{1}{x^2 + 2x} + \frac{4x^2 - x - 3}{x^2 + 2x - 3} &= \frac{1}{x(x + 2)} + \frac{(4x+3)(x-1)}{(x-1)(x+3)} \\ &= \frac{1}{x(x + 2)} + \frac{4x+3}{x+3} \\ &= \frac{x+3 + x(4x+3)(x+2)}{x(x + 2)(x+3)} \\ &= \frac{x+3 +x(4x^2 + 11x + 6)}{x(x + 2)(x+3)} \\ &= \frac{4x^3 + 11x^2 + 7x + 3}{x(x + 2)(x+3)} \end{align*}

\(\dfrac{b^2 + 6b + 9}{b^2-9} + \dfrac{b^2 - 6b + 8}{(b-2)(b+3)} + \dfrac{1}{b+3}\)

\begin{align*} \frac{b^2 + 6b + 9}{b^2-9} + \frac{b^2 - 6b + 8}{(b-2)(b+3)} + \frac{1}{b+3} &= \frac{(b+3)^2}{(b+3)(b-3)} + \frac{(b-4)(b-2)}{(b-2)(b+3)} + \frac{1}{b+3} \\ &= \frac{b+3}{b-3} + \frac{b-4}{b+3} + \frac{1}{b+3} \\ &= \frac{(b+3)^2 + (b-3)(b-4) + b -3}{(b-3)(b+3)} \\ &= \frac{b^2 + 6b + 9 + b^2 - 7b + 12 + b -3}{(b-3)(b+3)} \\ &=\frac{2b^2 + 18}{(b-3)(b+3)}\\ &= \frac{2(b^{2} + 9)}{(b-3)(b+3)} \end{align*}

\(\dfrac{x^{2} + 2x}{x^{2} + x + 6} \times \dfrac{x^{2} + 2x + 1}{x^{2} + 3x + 2}\)

\begin{align*} \frac{x^2 + 2x}{x^2 + x + 6} \times \frac{x^2 + 2x + 1}{x^2 + 3x + 2} &=\frac{x(x + 2)}{x^2 + x + 6} \times \frac{(x + 1)(x + 1)}{(x + 2)(x + 1)}\\ &= \frac{x(x + 1)}{x^2 + x + 6} \end{align*}

\(\dfrac{12}{z+12} + \dfrac{5}{z-5}\)

\begin{align*} \frac{12}{z+12} + \frac{5}{z-5} &= \frac{12(z-5) + 5(z+12)}{(z+12)(z-5)}\\ &= \frac{12z-60 + 5z+60}{(z+12)(z-5)}\\ &= \frac{17z}{(z+12)(z-5)} \end{align*}

\(\dfrac{11}{w-11} - \dfrac{4}{w-4}\)

\begin{align*} \frac{11}{w-11} - \frac{4}{w-4} \\ &= \frac{11(w-4) - 4(w-11)}{(w-11)(w-4)}\\ &= \frac{11w-44 - 4w+44}{(w-11)(w-4)}\\ &= \frac{7w}{(w-11)(w-4)} \end{align*}

Show that \((2x - 1)^{2} - (x - 3)^{2}\) can be simplified to \((x + 2)(3x - 4)\).

\begin{align*} (2x - 1)^{2} - (x - 3)^{2} & = (2x - 1)(2x - 1) - (x - 3)(x - 3) \\ &= 4x^2 - 2x - 2x + 1 - (x^2 - 3x - 3x - 9)\\ &= 3x^2 + 2x - 8\\ &=(3x - 4)(x + 2) \end{align*}

What must be added to \(x^{2} - x + 4\) to make it equal to \((x + 2)^{2}\)?

Suppose \(A\) must be added to the expression to get the desired result.

\begin{align*} \therefore (x^2 - x + 4) + A &= (x + 2)^2\\ \therefore A &= (x + 2)(x + 2) - (x^2 - x + 4)\\ & = x^2 + 2x + 2x + 4- x^2 + x - 4\\ & = 5x \end{align*}

Therefore \(5x\) must be added.

Evaluate \(\dfrac{x^{3} + 1}{x^{2} - x + 1}\) if \(x = \text{7,85} \text{ without using a calculator. Show your work.}\)

First simplify the expression:

\begin{align*} \frac{x^{3} + 1}{x^{2} - x + 1} & = \frac{(x + 1)(x^2 - x + 1)}{x^2 - x + 1} \\ & = x + 1 \end{align*}

Now substitute the value of \(x\): \(\text{7,85} + 1 = \text{8,85}\).

With what expression must \((a - 2b)\) be multiplied to get a product of \((a^{3} - 8b^{3})\)?

\[(a - 2b)(a^2 + 2ab + 4b^2) = a^3 - 8b^3\]

So, the expression is \(a^2 + 2ab + 4b^2\).

With what expression must \(27x^{3} + 1\) be divided to get a quotient of \(3x + 1\)?

\begin{align*} 27x^3 + 1 & = (3x + 1)(9x^2 - 3x + 1)\\ \frac{(3x + 1)(9x^2 - 3x + 1)}{9x^2 - 3x + 1} &= 3x + 1 \end{align*}

Therefore the expression is \(9x^2 - 3x + 1\).

\(\dfrac{4}{3x^2 + 2x - 1}\)

\begin{align*} \frac{4}{3x^2 + 2x - 1} &= \frac{4}{(3x - 1)(x+1)} \\ x \ne \frac{1}{3} &\text{ and } x \ne -1 \end{align*}

\(\dfrac{a}{3(b-a) + ab - a^2}\)

\begin{align*} \frac{a}{3(b-a) + ab - a^2} &= \frac{a}{3(b-a) + a(b-a)} \\ &=\frac{a}{(b-a)(a+3)} \\ a \ne b &\text { and } a \ne -3 \end{align*}

1.9 Chapter summary

Table of Contents

2.1 Introduction