\(2y(y+4)\)
1.6 Products
|
Previous
1.5 Estimating surds
|
Next
1.7 Factorisation
|
1.6 Products (EMAB)
Mathematical expressions are just like sentences and their parts have special names. You should be familiar with the words used to describe the parts of mathematical expressions. These words are given in the table below, using the following expression as an example:
\[3{x}^{2} + (7xy)^{3} - {125}\]|
Name |
Examples |
|
term |
\(3{x}^{2} \; ; \; (7xy)^{3} \; ; \; -125\) |
|
expression |
\(3{x}^{2} + (7xy)^{3} - {5}^{3}\) |
|
coefficient |
\(3 \; ; \; 7\) |
|
exponent |
\(2 \; ; \; 3\) |
|
base |
\(x \; ; \; 7xy \) |
|
constant |
\(-125\) |
|
variable |
\(x \; ; \; y\) |
|
equation |
\(3{x}^{2} + (7xy)^{3} - 125 = 0\) |
Multiplying a monomial and a binomial (EMAC)
A monomial is an expression with one term, for example, \(3x\) or \({y}^{2}\). A binomial is an expression with two terms, for example, \(ax+b\) or \(cx+d\).
Worked example 7: Simplifying brackets
Simplify: \[2a\left(a - 1\right) - 3\left({a}^{2} - 1\right)\]
Multiplying two binomials (EMAD)
Here we multiply (or expand) two linear binomials:
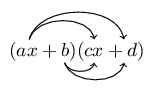
Worked example 8: Multiplying two binomials
Find the product: \(\left(3x-2\right)\left(5x+8\right)\)
The product of two identical binomials is known as the square of the binomial and is written as:
\[{\left(ax + b\right)}^{2} = {a}^{2}{x}^{2} + 2abx + {b}^{2}\]If the two terms are of the form \(ax + b\) and \(ax - b\) then their product is:
\[\left(ax + b\right)\left(ax - b\right) = {a}^{2}{x}^{2} - {b}^{2}\]This product yields the difference of two squares.
Multiplying a binomial and a trinomial (EMAF)
A trinomial is an expression with three terms, for example, \(a{x}^{2} + bx + c\). Now we can learn how to multiply a binomial and a trinomial.
To find the product of a binomial and a trinomial, multiply out the brackets:
\[\left(A + B\right)\left(C + D + E\right) = A\left(C + D + E\right) + B\left(C + D + E\right)\]This video shows some examples of multiplying a binomial and a trinomial.
Worked example 9: Multiplying a binomial and a trinomial
Find the product: \(\left(x - 1\right)\left({x}^{2} - 2x + 1\right)\)
Expand the bracket
\[\left(x - 1\right)\left({x}^{2} - 2x + 1\right) = x\left({x}^{2} - 2x + 1\right) - 1\left({x}^{2} - 2x + 1\right) = {x}^{3} - 2{x}^{2} + x - {x}^{2} + 2x - 1\]Simplify
\[{\left(x - 1\right)\left({x}^{2} - 2x + 1\right)} = {x}^{3} - 3{x}^{2} + 3x - 1\]Expand the following products:
\((y+5)(y+2)\)
\((2 - t)(1 - 2t)\)
\((x - 4)(x + 4)\)
\(-(4 - x)(x + 4)\)
\(-(a + b)(b - a)\)
\((2p + 9)(3p + 1)\)
\((3k - 2)(k + 6)\)
\((s + 6)^{2}\)
\(-(7 - x)(7 + x)\)
\((3x - 1)(3x + 1)\)
\((7k + 2)(3 - 2k)\)
\((1 - 4x)^{2}\)
\((-3 - y)(5 - y)\)
\((8 - x)(8 + x)\)
\((9 + x)^{2}\)
\((-7y + 11)(-12y + 3)\)
\((g - 5)^2\)
\begin{align*} (g - 5)^2 & = (g - 5)(g - 5) \\ & = g^2 - 5g - 5g + 25 \\ & = g^2 - 10g + 25 \end{align*}
\((d + 9)^2\)
\begin{align*} (d + 9)^2 & = (d + 9)(d + 9) \\ & = d^2 + 9d + 9d + 81\\ & = d^2 + 18d + 81 \end{align*}
\((6d + 7)(6d - 7)\)
\begin{align*} (6d + 7)(6d - 7) & = 36d^{2} - 42d + 42d - 49\\ &= 36d^{2} - 49 \end{align*}
\((5z + 1)(5z - 1)\)
\begin{align*} (5z + 1)(5z - 1) &= 25z^2 - 5z + 5z -1 \\ & = 25z^{2} - 1 \end{align*}
\((1 - 3h)(1 + 3h)\)
\begin{align*} (1 - 3h)(1 + 3h) &= 1 + 3h - 3h -9h^{2}\\ &= 1 - 9h^{2} \end{align*}
\((2p + 3)(2p + 2)\)
\begin{align*} (2p + 3)(2p + 2) &= 4p^2 + 4p + 6p + 6 \\ &= 4p^2 + 10p + 6 \end{align*}
\((8a + 4)(a + 7)\)
\begin{align*} (8a + 4)(a + 7) &= 8a^2 + 56a + 4a + 28 \\ &= 8a^{2} + 60a + 28 \end{align*}
\((5r + 4)(2r + 4)\)
\begin{align*} (5r + 4)(2r + 4) &= 10r^{2} + 20r + 8r + 16 \\ &= 10r^{2} + 28r + 16 \end{align*}
\((w + 1)(w - 1)\)
\begin{align*} (w + 1)(w - 1) &= w^2 + w - w - 1\\ &= {w}^2 - 1 \end{align*}
Expand the following products:
\((g + 11)(g - 11)\)
\begin{align*} (g + 11)(g - 11) & = g^2 + 11g - 11g - 121\\ & = g^2 - \text{121} \end{align*}
\((4b - 2)(2b - 4)\)
\begin{align*} (4b - 2)(2b - 4) & = 8b^{2} - 16b - 4b + 8 \\ &= 8b^{2} - 20b + 8 \end{align*}
\((4b - 3)(2b - 1)\)
\begin{align*} (4b - 3)(2b - 1) &= 8b^{2} - 4b - 6b + 3 \\ &= 8b^{2} - 10b + 3 \end{align*}
\((6x - 4)(3x + 6)\)
\begin{align*} (6x - 4)(3x + 6) &= 18x^{2} + 36x - 12x -24 \\ &= 18x^{2} + 24x - 24 \end{align*}
\((3w - 2)(2w + 7)\)
\begin{align*} (3w - 2)(2w + 7) &= 6w^{2} + 21w - 4 w - 14 \\ &= 6w^{2} + 17w - 14 \end{align*}
\((2t - 3)^2\)
\begin{align*} (2t - 3)^2 & = (2t - 3)(2t - 3) \\ & = 4t^{2} - 6t - 6t + 9 \\ &= 4t^{2} - 12t + 9 \end{align*}
\((5p - 8)^2\)
\begin{align*} (5p - 8)^2 & = (5p - 8)(5p - 8) \\ & = 25p^{2} - 40p - 40p + 64 \\ &= 25p^{2} - 80p + 64 \end{align*}
\((4y + 5)^2\)
\begin{align*} (4y + 5)^2 & = (4y + 5)(4y + 5) \\ & = 16 y^{2} + 20 y + 20 y + 25 \\ &= 16 y^{2} + 40y + 25 \end{align*}
\((2y^{6} + 3y^{5})(-5y - 12)\)
\(9(8y^{2} - 2y + 3)\)
\((-2y^{2} - 4y + 11)(5y - 12)\)
\((7y^{2} - 6y - 8)(-2y + 2)\)
\((10y + 3)(-2y^{2} - 11y + 2)\)
\((-12y - 3)(2y^{2} - 11y + 3)\)
\((-10)(2y^{2} + 8y + 3)\)
\((7y + 3)(7y^{2} + 3y + 10)\)
\(3m(9m^2 + 2) + 5m^2(5m + 6)\)
\begin{align*} 3m(9m^2 + 2) + 5m^2(5m + 6) &= 27m^3 + 6m + 25m^3 + 30m^2\\ &= 52m^3 + 6m + 30m^2 \end{align*}
\(4x^2(10x^3 + 4) + 4x^3(2x^2 + 6)\)
\begin{align*} 4x^2(10x^3 + 4) + 4x^3(2x^2 + 6) &= 40x^5 + 16x^2 + 8x^5 + 24x^3\\ &= 48x^5 + 16x^2 + 24x^3 \end{align*}
\(\text{3}{k}^3({k}^2 + \text{3}) + \text{2}{k}^2(\text{6}{k}^3 + \text{7})\)
\begin{align*} \text{3}{k}^3({k}^2 + \text{3}) + \text{2}{k}^2(\text{6}{k}^3 + \text{7}) & = \text{3}{k}^5 + \text{9}{k}^3 + \text{12}{k}^5 + \text{14}{k}^2\\ &= \text{15}{k}^5 + \text{9}{k}^3 + \text{14}{k}^2 \end{align*}
\((3x + 2)(3x - 2)(9x^2 - 4)\)
\((-6y^{4} + 11y^{2} + 3y)(y + 4)(y - 4)\)
\((x + 2)(x - 3)(x^2 + 2x - 3)\)
Expand the following products:
What is the value of \(b\), in \((x+b)(x-1)=x^2 + 3x - 4\)
From the constant term we see that \(b = 4\). We can check the \(x\) term: \(-x + 4x = 3x\).
What is the value of \(g\), in \((x-2)(x+g)=x^2 - 6x + 8\)
From the constant term we see that \(-2g = 8\), therefore \(g = -4\). We can check the \(x\) term: \(-4x - 2x = -6x\).
In \((x-4)(x+k) = x^2 + bx + c\):
For which of these values of \(k\) will \(b\) be positive?
\({-3 ; -1 ; 0 ; 3; 5}\)The \(x\) term is \(kx - 4x\) so for \(b\) to be positive \(k > 4\). Therefore \(k = 5\).
For which of these values of \(k\) will \(c\) be positive?
\({-3 ; -1 ; 0 ; 3; 5}\)The constant term is \(-4k\) so for \(c\) to be positive \(k < 0\). Therefore \(k = -3\) or \(k = -1\).
For what real values of \(k\) will \(c\) be positive?
From the previous question we see that \(k < 0\) will make \(c\) positive.
For what real values of \(k\) will \(b\) be positive?
From earlier we see that \(k > 4\) will make \(b\) positive.
Answer the following:
Expand \(\left(x + \dfrac{4}{x}\right)^2\).
Given that \(\left(x+ \dfrac{4}{x}\right)^2 = 14\), determine the value of \(x^2 + \dfrac{16}{x^2}\) without solving for \(x\).
Now we note that the above expression can also be written as \(x^2 + \dfrac{16}{x^2} + 8\). Since \(\left(x+ \dfrac{4}{x}\right)^2 = 14\) we get:
\begin{align*} 14 &= x^2 + 8 + \frac{16}{x^2} \\ 14 - 8 & = x^2 + \frac{16}{x^2} \\ 6 &= x^2 + \frac{16}{x^2} \end{align*}Answer the following:
Expand: \(\left(a+ \dfrac{1}{a}\right)^2\)
Given that \(\left(a+ \dfrac{1}{a}\right) = 3\), determine the value of \(\left(a+ \dfrac{1}{a}\right)^2\) without solving for \(a\).
Given that \(\left(a - \dfrac{1}{a}\right) = 3\), determine the value of \(\left(a+ \dfrac{1}{a}\right)^2\) without solving for \(a\).
We note that:
\[\left(a + \frac{1}{a}\right)^2 = a^2 + 2 + \frac{1}{a^2}\] \[\left(a - \frac{1}{a}\right)^2 = a^2 - 2 + \frac{1}{a^2}\]Next we note that if we add 4 to \(\left(a - \dfrac{1}{a}\right)^2\) we get \(\left(a + \dfrac{1}{a}\right)^2\). Therefore:
\begin{align*} \left(a + \frac{1}{a}\right)^2 &= a^2 - 2 + \frac{1}{a^2} + 4 \\ & = 3^{2} + 4 \\ &= 9 + 4 \\ &= 13 \end{align*}Answer the following:
Expand: \(\left(3y+ \dfrac{1}{2y}\right)^2\)
Given that \(3y+ \dfrac{1}{2y} =4\), determine the value of \(\left(3y+ \dfrac{1}{2y}\right)^2\) without solving for \(y\).
Answer the following:
Expand: \(\left(a + \dfrac{1}{3a}\right)^2\)
Expand: \(\left(a + \dfrac{1}{3a}\right)\left(a^2 - \dfrac{1}{3} + \dfrac{1}{9a^2}\right)\)
Given that \(a + \dfrac{1}{3a} = 2\), determine the value of \(a^3 + \dfrac{1}{27a^3}\) without solving for \(a\).
|
Previous
1.5 Estimating surds
|
Table of Contents |
Next
1.7 Factorisation
|
