How many pieces of wood should Robert expect to find in the box that the cabinet came in?
\(\text{5}\) pieces
|
Previous
10.4 Packaging and models
|
Next
11.1 Introduction and key concepts
|
Robert buys a new TV cabinet that comes with the following pictoral assembly instructions:
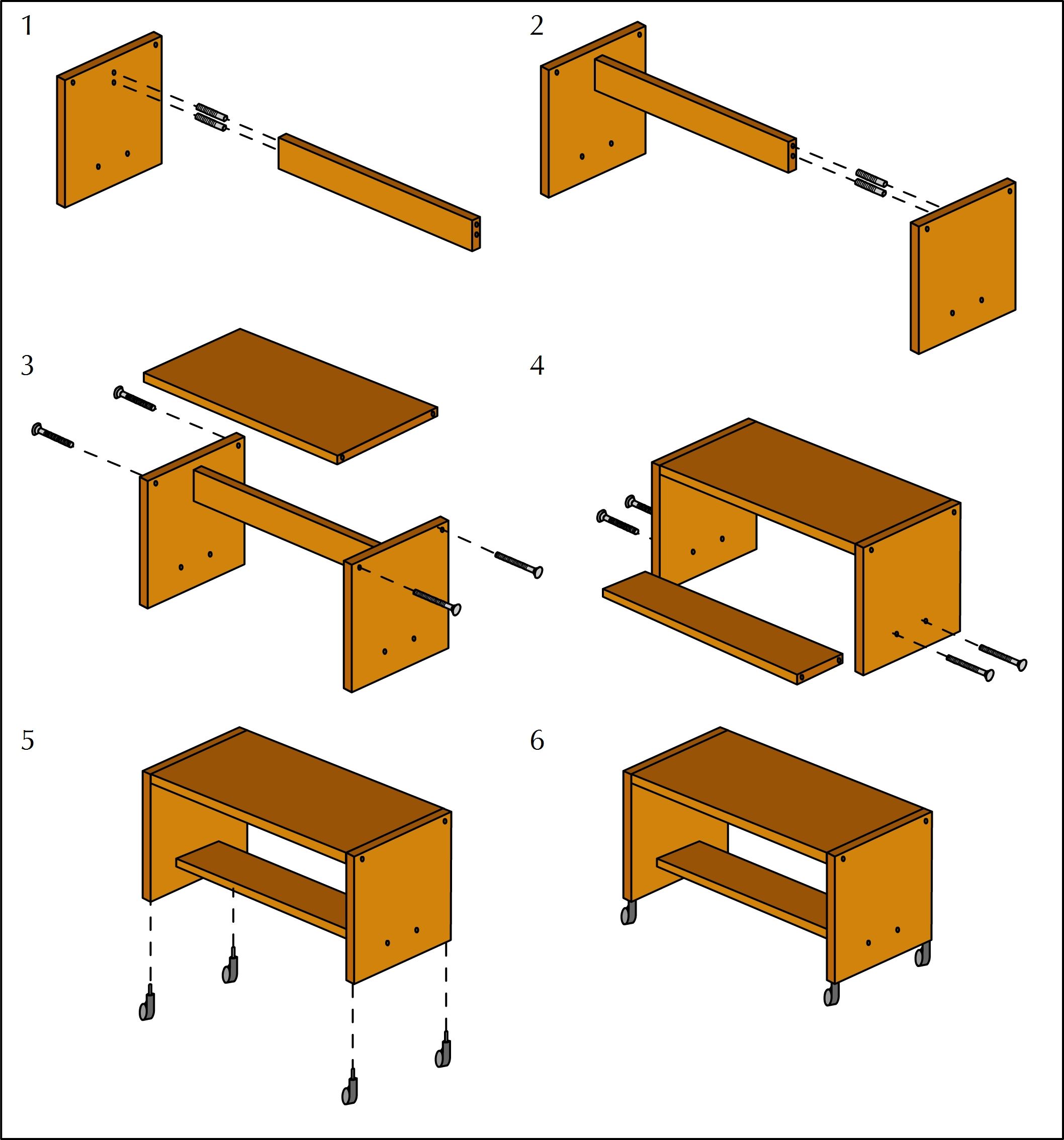
How many pieces of wood should Robert expect to find in the box that the cabinet came in?
\(\text{5}\) pieces
How many wheels should be in the box?
\(\text{4}\) wheels
If the cabinet did not come with screws, how may screws will Robert need to put the cabinet together?
\(\text{12}\) screws
The assembly diagram does not indicate what tools Robert may need. List two tools you think he may need to assemble the cabinet.
He will need a screwdriver and possibly a hammer
For each step (1 - 6) give a written description explaining what to do.
1. Screw the cabinet top support piece into the left side panel of the cabinet. 2. screw the top support piece into the right side panel of the cabinet. 3. Attach the top of the cabinet to the sides, screwing it in. 4. Slide the bottom piece into the cabinet. Screw it in place. 5. Attach the wheels to the base of the cabinet. 6. The cabinet assembly is complete!
Could the cabinet be assembled if Robert completes the steps in a different order? Explain your answer.
Yes. Robert could assemble it in a different order (e.g. he could put the bottom piece in before the top piece) but it will probably be more difficult.
You are given the plan below for William's flat.
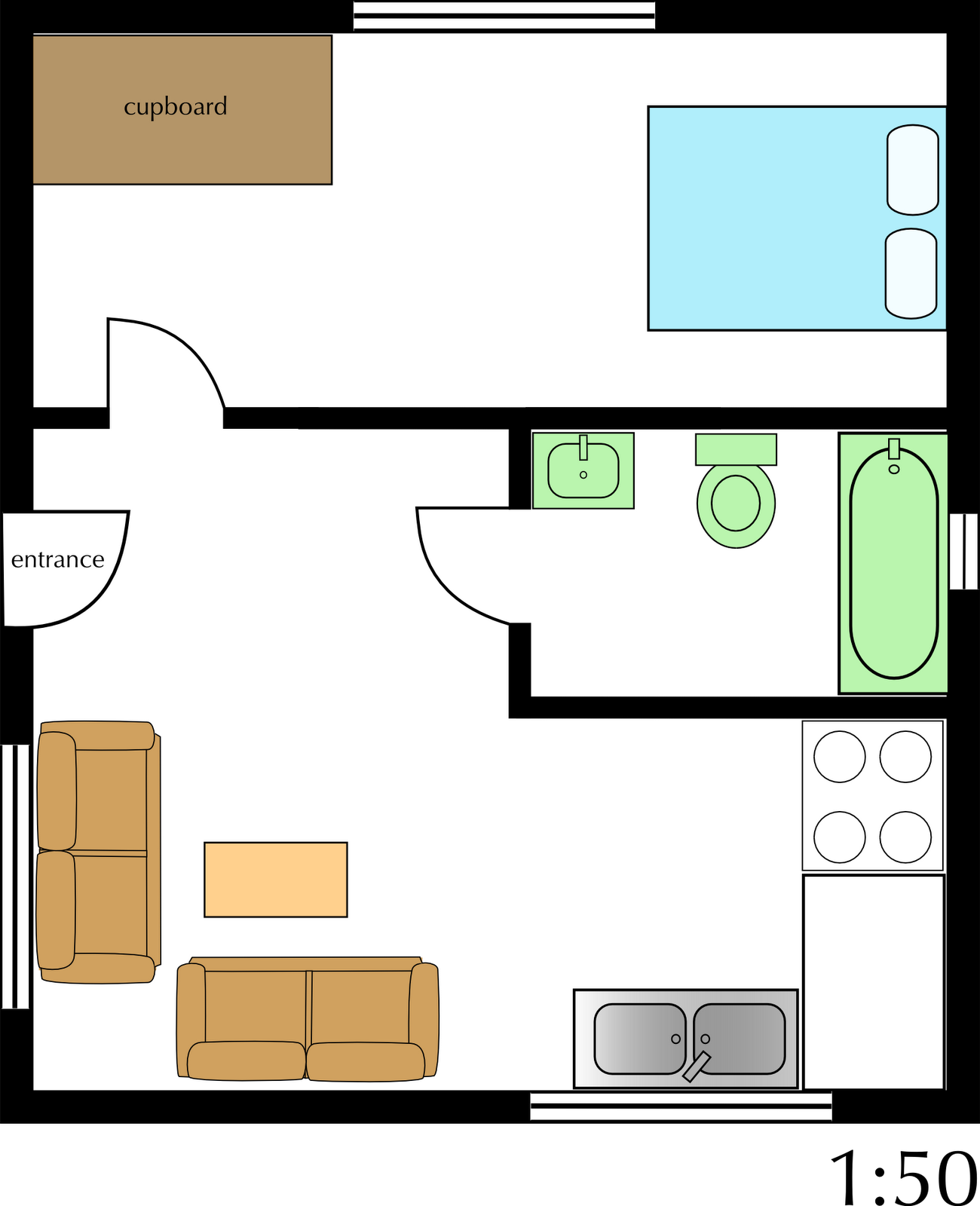
Identify five symbols used on this plan.
Stove, kitchen sink, couches, doors, windows, toilet, bath, basin, bed etc.
If the diagram above has been drawn on a scale of \(\text{1}\) : \(\text{50}\), complete the following table showing all calculations:
Measurement on plan | Calculation | Measurement in real life | |
Bath (width) | |||
Bath (length) | |||
Main bedroom window (length) | |||
Kitchen sink (width) | |||
Bedroom (length) | |||
Bedroom (width) |
Measurement on plan | Calculation | Measurement in real life | |
Bath (width) | \(\text{1,5}\) \(\text{cm}\) | \(\text{1,5}\) \(\text{cm}\) \(\times\) \(\text{50}\) | \(\text{75}\) \(\text{cm}\) |
Bath (length) | \(\text{3,5}\) \(\text{cm}\) | \(\text{3,5}\) \(\text{cm}\) \(\times\) \(\text{50}\) | \(\text{175}\) \(\text{cm}\) |
Main bedroom window (length) | \(\text{4}\) \(\text{cm}\) | \(\text{4}\) \(\text{cm}\) \(\times\) \(\text{50}\) | \(\text{200}\) \(\text{cm}\) |
Kitchen sink (width) | \(\text{3}\) \(\text{cm}\) | \(\text{3}\) \(\text{cm}\) \(\times\) \(\text{50}\) | \(\text{150}\) \(\text{cm}\) |
Bedroom (length) | \(\text{12}\) \(\text{cm}\) | \(\text{12}\) \(\text{cm}\) \(\times\) \(\text{50}\) | \(\text{600}\) \(\text{cm}\) |
Bedroom (width) | \(\text{5}\) \(\text{cm}\) | \(\text{5}\) \(\text{cm}\) \(\times\) \(\text{50}\) | \(\text{250}\) \(\text{cm}\) |
William wants to put tiles on the floor in the bedroom. Calculate how many m\(^{\text{2}}\) of tiles he will need.
Dimensions = \(\text{600}\) \(\text{cm}\) \(\times\) \(\text{250}\) \(\text{cm}\) = \(\text{6}\) \(\text{m}\) \(\times\) \(\text{2,5}\) \(\text{m}\) = \(\text{15}\) \(\text{m}\)\(^{\text{2}}\)
Calculate the cost of the tiles if one box contains \(\text{3}\) \(\text{m}\)\(^{\text{2}}\) worth of tiles and costs \(\text{R}\,\text{120}\).
\(\text{15}\) \(\text{m}\)\(^{\text{2}}\) \(\div\) \(\text{3}\) = \(\text{5}\) boxes. \(\text{5}\) \(\times\) \(\text{R}\,\text{120}\) = \(\text{R}\,\text{600}\)
William's landlord is charging him \(\text{R}\,\text{90}\) per m\(^{\text{2}}\) for the flat. How much is his rent in total?
Dimensions of flat = \(\text{12}\) \(\times\) \(\text{15}\) \(\text{cm}\) = \(\text{50}\)(\(\text{12}\) \(\times\) \(\text{50}\)) = \(\text{600}\) \(\text{cm}\) \(\times\) \(\text{750}\) \(\text{cm}\) = \(\text{6}\) \(\text{m}\) \(\times\) \(\text{7,5}\) \(\text{m}\). So area = \(\text{45}\) \(\text{m}\)\(^{\text{2}}\). \(\text{R}\,\text{90}\) \(\times\) \(\text{45}\) \(\text{m}\)\(^{\text{2}}\) = \(\text{R}\,\text{4 050}\)
For a birthday present William is given a new couch. The couch is \(\text{1,2}\) \(\text{m}\) wide and \(\text{2,5}\) \(\text{m}\) long. Will he be able to fit it through the front door of the flat?
Door is \(\text{1,5}\) \(\text{cm}\) wide. \(\text{1,5}\) \(\times\) \(\text{50}\) = \(\text{75}\) \(\text{cm}\). No - the new couch will not be able to fit through the front door.
The following plan is your friend's current layout for their kitchen.
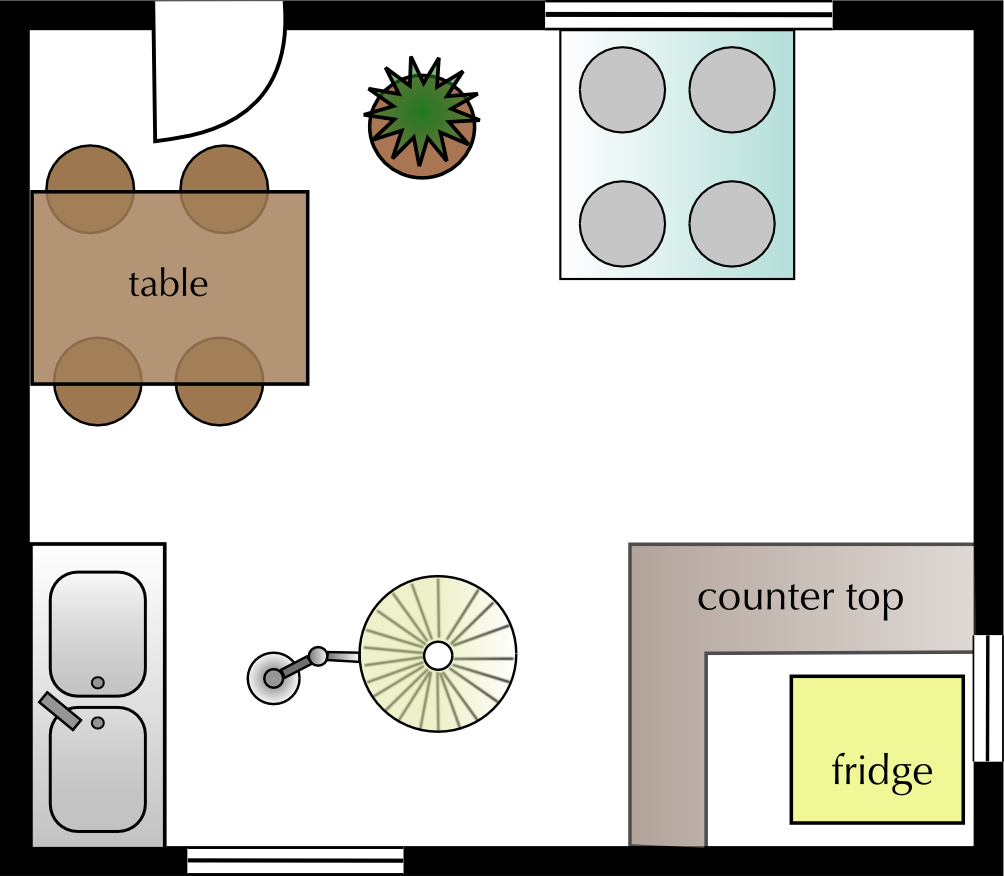
Identify five problems with this layout in terms of the placement of the items. Motivate your answer.
The stove is under the window (fire hazard if there are curtains), the door opens into the table and chairs, The fridge is inaccessible, there is a lamp in the middle of the floor and a pot plant in the middle of the floor.
Redraw the plan with an improved layout. All the elements present in the original diagram must be included in the improved plan.
Learner-dependent answer, but all the objects in the original diagram must be included and the layout problems must be resolved.
You want to post a package to your friend who lives in Botswana. The contents are a brand of chocolate that your friend is struggling to find in the shops where they live. The following diagram shows what the chocolate looks like.

You have to fit as many of the chocolates as possible into a rectangular cardboard box which is twice as long as it is wide.
Suggest at least four different ways that these chocolates can be packed. Make a sketch to illustrate each method.
There are a number of combinations that can be used (e.g. vertically, horizontally, long side parallel or perpendicular to width of box).
The chocolates weigh \(\text{100}\) \(\text{g}\) each. If the maximum capacity of the cardboard box is \(\text{2,5}\) \(\text{kg}\), how many of the chocolates can you pack?
\(\text{2,5}\) \(\text{kg}\) = \(\text{2 500}\) \(\text{g}\). \(\text{2 500}\) \(\div\) \(\text{100}\) \(\text{g}\)= \(\text{25}\) chocolates.
If each chocolate costs \(\text{R}\,\text{11,99}\), and you buy enough chocolates to fill the box to it's maximum weight, how much will you spend on chocolates?
\(\text{25}\) \(\times\) \(\text{R}\,\text{11,99}\) = \(\text{R}\,\text{299,75}\)
If the cardboard box cost you \(\text{R}\,\text{10,00}\), and shipping to Botswana costs \(\text{R}\,\text{40}\) per kg, how much will the parcel cost you in total, including the cost of the chocolates? Assume that the box weighs \(\text{2,5}\) \(\text{kg}\).
Total cost = cost of chocolates + cost of box + cost of shipping = \(\text{R}\,\text{299,75}\) + \(\text{R}\,\text{10,00}\) + (\(\text{R}\,\text{40}\) \(\times\) \(\text{2,5}\) \(\text{kg}\)) = \(\text{R}\,\text{409,75}\)
What will be easier to pack: cylinders or triangular prisms? Give a reason for your answer.
Triangular prisms are easier to pack because they have flat sides, so there will not be gaps between the chocolates.
|
Previous
10.4 Packaging and models
|
Table of Contents |
Next
11.1 Introduction and key concepts
|