If Jason's household uses \(\text{140}\) kWh of electricity in a month, calculate what his electricity bill will be, in Rands.
\(\text{140}\) \(\times\) \(\text{129,05}\) \(\text{c}\) = \(\text{18 067}\) \(\text{c}\) = \(\text{R}\,\text{180,67}\)
|
Previous
4.2 Financial documents
|
Next
End of chapter activity
|
Tariffs are pre-determined rates that are used to determine how much money you owe for a given service. For example, the total amount of money you owe on your municipal bill is calculated using predetermined tariffs. A tariff usually includes a unit of payment with a unit of measurement - for example cell phone bills are charged in cents or rands per minute (R/minute) and electricity is charged in cents per kilowatt hour or c/kWh. Telkom charges monthly landline rental in Rands per month.
In this section you will work with different tariff systems, learn how to calculate costs using given tariffs and how to draw and interpret graphs of various tariff systems.
Municipal tariffs include tariffs for electricity, water and refuse removal. They differ from one city to the next, but generally speaking, the more electricity or water you use in a month, the more expensive it is per unit. Sometimes municipal tariffs are also called “rates”. Your municipal bill also usually includes a monthly property rate based on the municipal value of your house - again, the more your house is worth, the more you will pay in rates.
The City of Durban's Ethekwini Municipality charges the following tariffs for domestic water usage in 2013, for properties valued at more than \(\text{R}\,\text{250 000}\):
Price per kilolitre, excluding VAT | |
\(\text{0}\) \(\text{kl}\) to \(\text{9}\) \(\text{kl}\) | \(\text{R}\,\text{9,50}\) |
from \(\text{9}\) \(\text{kl}\) to \(\text{25}\) \(\text{kl}\) | \(\text{R}\,\text{11,22}\) |
From \(\text{25}\) \(\text{kl}\) to \(\text{30}\) \(\text{kl}\) | \(\text{R}\,\text{14,95}\) |
from \(\text{30}\) \(\text{kl}\) to \(\text{45}\) \(\text{kl}\) | \(\text{R}\,\text{23,05}\) |
more than \(\text{45}\) \(\text{kl}\) | \(\text{R}\,\text{25,36}\) |

Megan's monthly water consumption is \(\text{12}\) \(\text{kl}\). Calculate her monthly water costs, excluding VAT.
Gilbert's monthly water consumption is \(\text{32}\) \(\text{kl}\).
Study the following graph, showing the relationship between the quantity of water used and the price per unit, as given in the above table: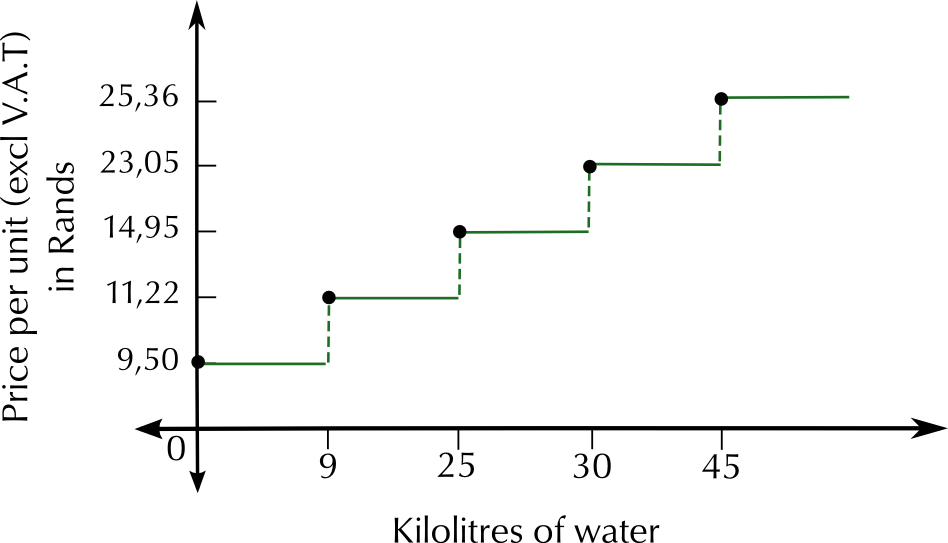 Why do you think the graph is a series of horizontal lines and sudden vertical rises?
Why do you think the graph is a series of horizontal lines and sudden vertical rises?
Domestic electricity in the City of Cape Town is charged for using the tariffs below, for households who use more than \(\text{450}\) kWh of electricity per month. They refer to each category of electricity usage as a block, and the tariffs are charged in cents per kilowatt hour (kWh). VAT is included in the tariff costs listed below.
Block number (kWh) | cents per kWh (incl VAT) |
Block 1 (\(\text{0}\) - \(\text{150}\) kWh) | \(\text{129,05}\) |
Block 2 (\(\text{150,1}\) - \(\text{350}\) kWh) | \(\text{134,65}\) |
Block 3 (\(\text{350,1}\) - \(\text{600}\) kWh) | \(\text{134,65}\) |
Block 4 (\(>\) \(\text{600}\) kWh) | \(\text{159,81}\) |
If Jason's household uses \(\text{140}\) kWh of electricity in a month, calculate what his electricity bill will be, in Rands.
\(\text{140}\) \(\times\) \(\text{129,05}\) \(\text{c}\) = \(\text{18 067}\) \(\text{c}\) = \(\text{R}\,\text{180,67}\)
Thomas uses \(\text{200,5}\) kWh of electricity in a month. What will his electricity costs be in Rands?
Block \(\text{1}\):\(\text{140}\) \(\times\) \(\text{129,05}\) \(\text{c}\) = \(\text{18 067}\) \(\text{c}\) = \(\text{R}\,\text{180,67}\). Block \(\text{2}\): \(\text{200,5}\) - \(\text{140}\) = \(\text{60,5}\) kWh. \(\text{60,5}\) \(\times\) \(\text{134,65}\) \(\text{c}\) = \(\text{8 146,325}\) \(\text{c}\) = \(\text{R}\,\text{81,46325}\). \(\text{R}\,\text{180,67}\) + \(\text{R}\,\text{81,4572}\) = \(\text{R}\,\text{262,13325}\) \(\approx\) \(\text{R}\,\text{262,13}\)
The City of Cape Town decides to introduce a fixed additional tariff for anyone who uses more than \(\text{350}\) kWh of electricity. This fixed cost is \(\text{R}\,\text{24,45}\) per month. (I.e. the cost is \(\text{R}\,\text{24,45}\) plus the price per units used). If Neil uses \(\text{423}\) kWh of electricity in a month, calculate what his total electricity cost will be.

Basic cost: \(\text{R}\,\text{24,45}\). Block \(\text{1}\):\(\text{140}\) \(\times\) \(\text{129,05}\) \(\text{c}\) = \(\text{18 067}\) \(\text{c}\) = \(\text{R}\,\text{180,67}\). Block \(\text{2}\): \(\text{350}\) - \(\text{150,1}\) = \(\text{199,99}\) kWh. \(\text{199,99}\) \(\times\) \(\text{134,65}\) \(\text{c}\) = \(\text{26 928,6535}\) \(\text{c}\) = \(\text{R}\,\text{269,286535}\). Block \(\text{3}\): \(\text{423}\) kWh - \(\text{350,1}\) kWh = \(\text{72,9}\) kWh. \(\text{72,9}\) \(\times\) \(\text{134,65}\) \(\text{c}\) = \(\text{9 815,985}\) \(\text{c}\) = \(\text{R}\,\text{98,15985}\). \(\text{R}\,\text{24,45}\) + \(\text{R}\,\text{180,67}\) + \(\text{R}\,\text{269,286535}\) + \(\text{R}\,\text{98,15985}\) = \(\text{R}\,\text{572,566385}\) \(\approx\) \(\text{R}\,\text{572,57}\).
Fixed phone line and cell phone service providers also commonly charge you for calls using tariffs. The tariff cost can be influenced by factors like the distance of the call (e.g. calls overseas are always more expensive than local calls) and the time of day (most service providers offer cheaper rates in the evenings, depending on which phone package you use).
Telkom charges for normal, national landline calls according to the following tariffs:
Distance | Basic, fixed charge in Rands (incl. VAT) (regardless of length of call or distance) | Rands per second (incl. VAT) | Rands per second (incl. VAT) |
All times | Standard Time: Mon - Fri 07:00 to 19:00 | Callmore time: Mon to Fri 19:00 - 7:00 and Fri 19:00 - Mon 7:00 | |
Local (\(\text{0}\) - \(\text{50}\) \(\text{km}\)) | \(\text{0,570}\) | \(\text{0,00700}\) | \(\text{0,00344}\) |
Long distance (\(>\)\(\text{50}\) \(\text{km}\)) | \(\text{0,570}\) | \(\text{0,00950}\) | \(\text{0,00475}\) |
Davina calls her mother, who lives \(\text{25}\) \(\text{km}\) away, during standard time.
Karabo calls his friend at 5 p.m. on a Saturday. They chat for \(\text{10}\) minutes. If his friend lives \(\text{5}\) \(\text{km}\) away, calculate how much the call with cost Karabo.
A local cellular provider charges the following for a standard contract:
Monthly subscription: \(\text{R}\,\text{100}\)
Mandatory itemised billing: \(\text{R}\,\text{22}\)
Calls and SMS's are charged for using the tariffs given below. This service provider uses per second billing, so the tariff is Rands per \(\text{60}\) seconds of call time, even if those \(\text{60}\) seconds are split over two or more calls. Assume that these tariffs, or rates, and the monthly subscription are VAT inclusive. (An SMS is a text message, and an MMS is a text and data message, that may include a photo, for example).
Rate per minute for the first \(\text{5}\) minutes of the day | \(\text{R}\,\text{1,95}\) |
Rate per minute (\(\text{60}\) seconds) thereafter | \(\text{R}\,\text{1,55}\) |
Calls to same network | \(\text{R}\,\text{0,99}\) per \(\text{60}\) seconds |
International SMS | \(\text{R}\,\text{1,20}\) per SMS |
SMS | \(\text{R}\,\text{0,60}\) per SMS |
MMS | \(\text{R}\,\text{0,75}\) per MMS |
Alfred has a contract like the one above. Assuming he does not use more than \(\text{R}\,\text{140}\) airtime in a month and \(\text{R}\,\text{40}\) worth of SMS's, what will his monthly cell phone bill cost?
Monthly subscription + itemised billing = \(\text{R}\,\text{122}\)
On the first day of the month, the first call Alfred makes is to his father (on a different network) and they talk for \(\text{2}\) minutes. How much will this call cost Alfred?
\(\text{R}\,\text{1,95}\) \(\times\) \(\text{2}\) = \(\text{R}\,\text{3,90}\)
On the same day, Alfred then calls his friend, Ivan. They talk for \(\text{4}\) minutes. How much will this second call cost him?
After the first call, Alfred has used \(\text{2}\) of the first \(\text{5}\) minutes of calls. The next call will cost (\(\text{3}\) \(\times\) \(\text{R}\,\text{1,95}\)) + (\(\text{1}\) \(\times\) \(\text{R}\,\text{1,55}\)) = \(\text{R}\,\text{7,40}\)
Later that afternoon, Alfred checks his phone and sees he has made \(\text{9}\) minutes, \(\text{25}\) seconds worth of calls.
How many seconds is this?
\(\text{9}\) minutes \(\text{25}\) seconds = (\(\text{9}\) \(\times\) \(\text{60}\) seconds) + \(\text{25}\) seconds = \(\text{565}\) seconds
If he now calls his friend Azra, who is on the same network, and they talk for \(\text{360}\) seconds, how much will the call cost him?
\(\text{360}\) seconds = \(\text{6}\) \(\times\) \(\text{60}\) seconds. Calls to the same network are \(\text{R}\,\text{0,99}\) per \(\text{60}\) seconds so it will cost \(\text{R}\,\text{0,99}\) \(\times\) \(\text{6}\) = \(\text{R}\,\text{5,94}\)
Two weeks later, Alfred has made \(\text{R}\,\text{70,45}\) worth of calls, sent \(\text{25}\) local SMS's, \(\text{5}\) international SMS's and \(\text{2}\) MMS's. Calculate how much airtime he has left.
Alfred starts with \(\text{R}\,\text{140}\) worth of airtime. We know he has spent \(\text{R}\,\text{70,45}\) on calls. The local sms's are covered by his monthly contract so we do not deduct them from his airtime (he will have \(\text{15}\) free local sms's left.) The \(\text{5}\) international sms's cost \(\text{5}\) \(\times\) \(\text{R}\,\text{1,20}\) = \(\text{R}\,\text{6,00}\) and the \(\text{2}\) MMS's cost \(\text{2}\) \(\times\) \(\text{R}\,\text{0,75}\) =\(\text{R}\,\text{1,50}\). Now we deduct all these costs from the initial amount or \(\text{R}\,\text{140}\): \(\text{R}\,\text{140}\) - \(\text{R}\,\text{70,45}\) - \(\text{R}\,\text{6,00}\) - \(\text{R}\,\text{1,50}\) = \(\text{R}\,\text{62,05}\). He has \(\text{R}\,\text{62,05}\) airtime left.
Alfred wants to buy an SMS bundle that he thinks is a good deal. With this bundle, he will get \(\text{125}\) SMS's for an extra \(\text{R}\,\text{78,75}\) per month (over and above the \(\text{40}\) free SMS's he already gets).
How much will each of the \(\text{125}\) SMS's in the new bundle cost him?
\(\text{R}\,\text{0,63}\)
Is this a better deal than what he currently pays for his non-free SMS's?
No. SMS's currently cost him only \(\text{R}\,\text{0,60}\), so the bundled SMS's are more expensive.
Alfred calls his sister for a big chat, and accidentally uses all of his \(\text{R}\,\text{140}\) airtime in one day (assume this happened at the beginning of the month and he did not send any SMS's). If she is on a different network, how long did they talk for? Round your answer to the nearest minute, and write it in hours and minutes.

The first \(\text{5}\) minutes cost: \(\text{R}\,\text{1,95}\) \(\times\) \(\text{5}\) = \(\text{R}\,\text{9,75}\). This leaves him with \(\text{R}\,\text{140}\) - \(\text{R}\,\text{9,75}\) = \(\text{R}\,\text{130,25}\) airtime. The remaining minutes will cost \(\text{R}\,\text{1,55}\) each. \(\text{R}\,\text{130,25}\) \(\div\) \(\text{R}\,\text{1,55}\) = \(\text{84}\) minutes = \(\text{1}\) hour and \(\text{24}\) minutes.
Transport tariffs work much the same as municipal and phone tariffs. They may apply to train travel, busses and taxis. Generally, transport tariffs are charged per unit of distance, and the further you need to travel, the higher the tariff and therefore the more expensive your ticket. Like some basic foods, transport fares for taxis, buses and trains in South Africa are exempt from VAT.
The municipal MyCiTi bus system in Cape Town charges the fares below. For all routes except the Airport route, you need to have a myconnect card. For the airport route, you can still use paper tickets, which you can buy at the bus stops at either end of the route.

Cost | Route name | |
\(\text{R}\,\text{23}\) | myconnect card | |
\(\text{R}\,\text{5,30}\) | Gardens - Civic Centre - Waterfront Big Bay - Table View - Parklands East Parklands East - Table View - Blouberg Sands Marine Circle - Table View - Blouberg Sands | F1 F14 F15 F16 |
\(\text{R}\,\text{10,60}\) | Table View - Civic Centre | T1 |
Free | Children under \(\text{1}\) \(\text{m}\) tall and under \(\text{4}\) years old | (all routes) |
Airport Service
Cost | Route name | |
\(\text{R}\,\text{57}\) | Civic Centre - Airport route | A1 |
\(\text{R}\,\text{28,10}\) | Civic Centre - Airport route for children 4 - 11 years old | A1 |
Free | Children under 1 metre tall and under \(\text{4}\) years old | A1 |
\(\text{R}\,\text{499,50}\) | Monthly ticket offering unlimited travel on the Airport - Civic Centre route (A1). This ticket cannot be used by anyone else and must have the name of the ticket holder on it. Write your name on the ticket as soon as buy it. | A1 |
Marissa's mother currently drives her to and from school and estimates that she spends \(\text{R}\,\text{13,62}\) on petrol per day, just for school lifts.
On average, Karen makes \(\text{5}\) round trips (from the airport to the Civic Centre and back again) in a month.
Metrorail in Gauteng charges the following tariffs for Metro (Standard) Class tickets for different zones:
Zone | Single | Return | Weekly | Monthly |
\(\text{1}\) - \(\text{19}\) \(\text{km}\) | \(\text{4,00}\) | \(\text{7,50}\) | \(\text{22,00}\) | \(\text{81,50}\) |
\(\text{20}\) - \(\text{29}\) \(\text{km}\) | \(\text{5,00}\) | \(\text{9,50}\) | \(\text{27,50}\) | \(\text{97,00}\) |
\(\text{30}\) - \(\text{39}\) \(\text{km}\) | \(\text{6,00}\) | \(\text{11,50}\) | \(\text{32,50}\) | \(\text{112,00}\) |
\(\text{40}\) - \(\text{49}\) \(\text{km}\) | \(\text{7,50}\) | \(\text{14,50}\) | \(\text{34,00}\) | \(\text{123,00}\) |
\(>\) \(\text{50}\) \(\text{km}\) | \(\text{9,50}\) | \(\text{18,50}\) | \(\text{38,50}\) | \(\text{140,00}\) |
Chuma travels \(\text{15}\) \(\text{km}\) on the train every day to school and back again. She buys a single ticket for every trip that she makes.
how many trips will Chuma make (to school and back) in one month (\(\text{4}\) weeks)?
\(\text{2}\) trips per day \(\times\) \(\text{5}\) school days per week \(\times\) \(\text{4}\) weeks = \(\text{40}\) trips per month
How much will this cost her, if she buys single tickets?
\(\text{40}\) \(\times\) \(\text{R}\,\text{4,00}\) = \(\text{R}\,\text{160,00}\)
How much cheaper will a monthly ticket be?
\(\text{R}\,\text{160,00}\) - \(\text{R}\,\text{81,50}\) = \(\text{R}\,\text{78,50}\) cheaper.
If she buys a monthly ticket for \(\text{R}\,\text{81,50}\), how much will each trip cost her?
\(\text{R}\,\text{81,50}\) \(\div\) \(\text{40}\) trips = \(\text{R}\,\text{2,04}\).
How much cheaper than a single ticket is this?
\(\text{R}\,\text{4,00}\) - \(\text{R}\,\text{2,04}\) = \(\text{R}\,\text{1,96}\) cheaper.
Lindiwe has a monthly ticket and travels a distance of \(\text{35}\) \(\text{km}\), return, every day.
How much does her monthly ticket cost her?
\(\text{R}\,\text{112,00}\)
Lindiwe's friend tells her that it's possible to get a \(\text{20}\%\) discount if you're a scholar, wearing your school uniform. What would her monthly ticket cost with a \(\text{20}\%\) discount?

\(\text{R}\,\text{112,00}\) \(\times\) \(\text{0,20}\) = \(\text{R}\,\text{22,40}\). \(\text{R}\,\text{112,00}\) - \(\text{R}\,\text{22,40}\) = \(\text{R}\,\text{89,60}\)
|
Previous
4.2 Financial documents
|
Table of Contents |
Next
End of chapter activity
|