Name three kinds of services included in this invoice.
Electricity, water, refuse sewerage, municipal rates
|
Previous
4.1 Introduction and key concepts
|
Next
4.3 Tariff systems
|
Household bills include municipal bills for electricity and water, telephone bills and shopping documents like till slips and account statements. You will receive a bill when you have used a service or utility (like electricity or a phone line) or made purchases using a store or credit card, which will require monthly payments on the outstanding balance. You will learn more about buying items on credit later in this chapter.

Some stores allow you to have a store account. You can then buy items “on your account”, without having to pay cash for them at the time. You will receive an account statement once a month, detailing what you bought, what you paid into the account (called credit) and what you still owe. Municipal bills work in much the same way - you use the services before you pay for them, and receive a monthly account detailing all your usage and the associated costs.
Many houses in South Africa have access to electricity, water and waste disposal (rubbish removal). These utilities and services are provided by the local government (municipality) and each household has to pay a monthly amount, depending on how much electricity and water was used. In this section we will look at municipal electricity and water bills.
The City of Johannesburg provided its residents with the following example of a municipal invoice, to explain to people how to read their municipal bills. Whilst no two municipalities send out identical bills, the kind of information provided in the document is usually very similar.

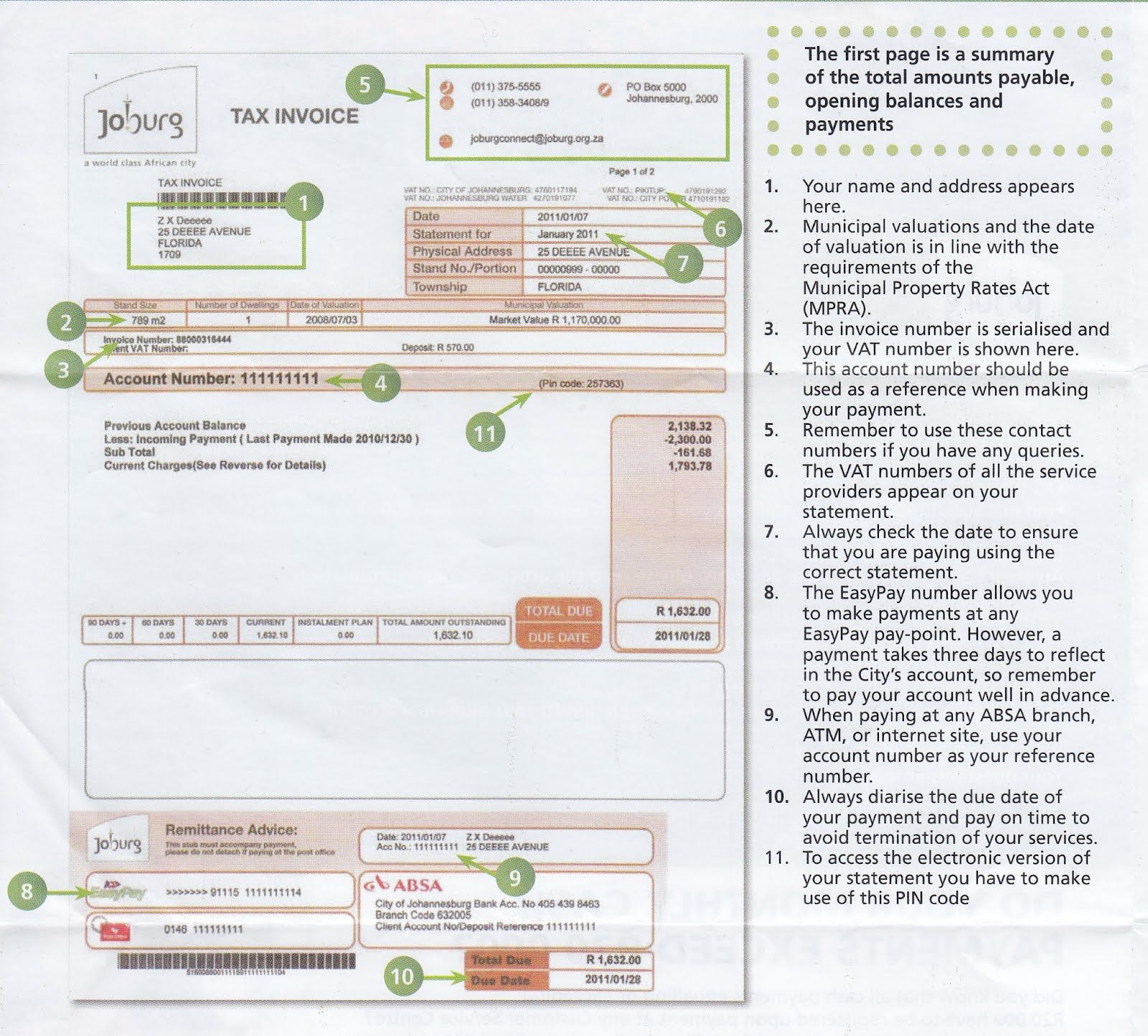
Joburg municipal bill, Page 1
As you can see from the above document (the first page of the bill), there are several important pieces of information included in this bill.
The second page of the bill looks as follows:

Joburg municipal bill, Page 2
Not all municipalities bundle together electricity, water and refuse charges in one account. It differs from one city to the next, but in some places you may get two separate bills - one for electricity and another for water and refuse, for example.

Also, invoices from different municipalities or companies will look different, and may use different terms to describe the same thing. You need to know a few more definitions before we move on to worked examples about municipal bills:
Look at the municipal bill below and answer the questions that follow:

In South Africa we get metered electricity and pre-paid electricity.
With metered electricity, you use first and pay later. The amount of electricity you use in a month is counted by an electricity meter - a special box that may be inside your house or outside on the property, that adds up all the units of electricity you use. Once a month a meter reader from the municipality will come to the house and read your meter and make a note of how much electricity you have used. This reading then gets uploaded to the system and you receive a bill for the electricity you used in that month.

Electricity meters outside a building
With pre-paid electricity, you pay first and use later. Much like cellphone airtime, you buy electricity vouchers (usually from your local shop) which you can then load into a special pre-paid meter at home. The pre-paid meter counts downwards, and shows you how many units worth of electricity you have left to use. No one from the municipality needs to read the meter, and you will not receive accounts because you have already paid for the electricity you have used. Pre-paid electricity is usually cheaper, per unit, than normal electricity. Buying it in advance can also make it easier to plan how much electricity you're going to use in a month, and how much you can afford to spend. However, it can be frustrating if you forget to buy a new voucher and you run out of electricity in the middle of cooking dinner!
Before you do the next worked example you need to know that electricity is measured in units called kilowatt hours (kWh), and it is charged for using set rates, or tariffs, in Rands per kWh. we shall study tariffs later in this chapter. In the meantime, you just need to understand that generally, the more electricity you use, the more expensive it becomes, per unit.
Mr du Plessis gets the account below for his electricity consumption over \(\text{2}\) months. He has three electricity meters on his property (let's assume there are two small houses and a flat on the premises) and they are billed for together. Study his invoice and answer the questions that follow.

The consumption levels for the first two meters listed (meter numbers 356413 and 382471) are fairly similar - they are both close to \(\text{3 000}\) kWh. The consumption level for the third meter (number 382709) is much lower, however.
The graph in the bottom left corner of the invoice shows the meter readings for Mr du Plessis' electricity consumption over the previous \(\text{12}\) months.
Mr Mukondwa receives the following municipal bill. Study the document and answer the questions that follow.
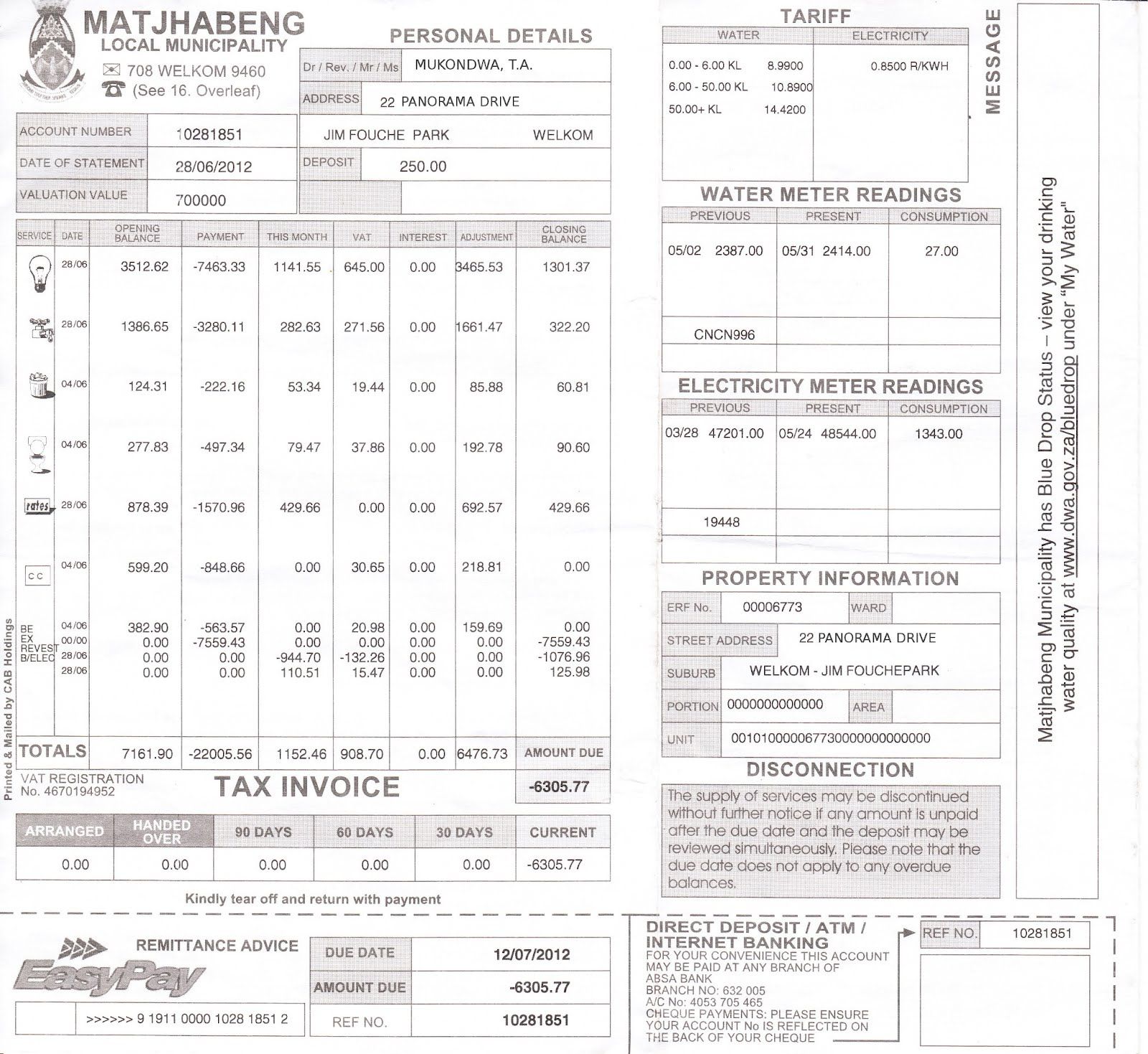
Name three kinds of services included in this invoice.
Electricity, water, refuse sewerage, municipal rates
Which service used costs the most on this invoice?
electricity
Name two different ways in which this invoice can be paid.
EasyPay, direct deposit, ATM, Internet banking
When is payment for this invoice due?
12/07/2012
What may happen if the invoice is not paid on time?
The services may be disconnected.
What is the total amount due?
\(-\)\(\text{R}\,\text{6 305,77}\)
Why is this a negative number?
Because Mr Mukondwa has already paid more money into the account (credit) than he owed, so he is \(\text{R}\,\text{6 305,77}\) in credit.
Is there any amount brought forward from the last invoice?
No. There are no outstanding amounts listed for the previous \(\text{30}\), \(\text{60}\) or\(\text{90}\) days.
Water consumption is typically measured in kilolitres (kl).
What is the consumption level of water on this invoice?
\(\text{27}\) \(\text{kl}\).
How much is this in litres?
\(\text{27 000}\) \(\ell\).
Mr Mukondwa thinks that the closing balance for his electricity consumption is much higher than normal.
What does this suggest?
Either he used much more electricity than usual, or there was a mistake with his electricity meter reading.
How many units of electricity were consumed in the previous month?
\(\text{1 343,00}\) kWh
Can Mr Mukondwa verify this in any way? Explain your answer.
Yes. He can check the meter himself and see if the reading corresponds to the reading the municipality took.
What should Mr Mukondwa do if he thinks the latest meter reading for his electricity is incorrect?
He should call the municipality and query the bill.
If your household has a fixed phone line or 'landline' (like those provided by Telkom and Neotel) or you have a cellphone on a contract (not “Pay-as-you-go”) you will receive monthly bills for these services that are much like the electricity and water bills we have just looked at.
It is also possible to have a prepaid landline. To use a prepaid landline, you simply buy a voucher and load the airtime onto your account, much like a prepaid cellphone account. Prepaid landlines are advantageous for people who don't have a credit record, or have a bad credit record, because you don't need a credit history or proof of employment and bank statements to have a prepaid fixed line. (A credit record shows how good you are about paying back money that you owe. If you are in debt and don't pay your bills, you will have a bad credit record.)
With phone bills for fixed lines, you are usually charged one fixed amount for rental of the phone line, and then for any calls you made. Call costs also vary depending on where you phone, as we shall see later in this chapter.
Look at the Telkom bill provided below and answer the questions that follow:

Different cellular providers in South Africa (like MTN, Vodacom, Cell C, 8ta and Virgin Mobile) offer different packages. You can have a contract with them, where you pay a monthly subscription and then pay for your calls and messages at the end of the month; or you can buy prepaid airtime upfront and then have the cost of your calls and messages deducted from that airtime.

Study the following MTN invoice and answer the questions that follow:

Oliver receives the following cell phone bill:

What is the balance brought forward from the previous invoice?
\(\text{R}\,\text{99,00}\)
On what date was the payment of this balance made?
02/07/2012
When is the payment for the current outstanding amount due?
31/07/2012
What subscription service does Oliver get for free?
HSDPA Voice Tariff
What subscription does Oliver get a full refund for?
VAS Balance Notification
What is the billing period for this invoice?
The month of July 2012
Oliver wants to query the last payment he made. List four things he could use as a reference number.
His cellphone number, his account number, the invoice number and the payment reference number.
Oliver wants to check that the VAT calculated on the total amount due is correct. Show how he can do this. Show all your calculations.
Total without VAT = \(\text{R}\,\text{86,84}\). \(\text{14}\%\) of this = \(\text{86,84} \times \frac{\text{14}}{\text{100}} = \text{12,1576} \approx\) \(\text{R}\,\text{12,16}\).
Every time you buy an item from a shop, you should receive a till slip indicating the value of the item you bought, how much money you offered the cashier for it, how much change you received and so on. Till slips come in many different forms depending on which shop you're buying things from. By law however, South African till slips must include:
It is important to know that VAT is not charged on some essential groceries in South Africa. These include: paraffin; brown bread; maize meal; samp; mealie rice; dried mealies; dried beans; lentils; tinned sardines; milk powder; milk, rice; vegetables; fruit; vegetable oil and eggs.
Boiketlo goes to buy her groceries at the Sunshine Superette. Study the till slip below and answer the questions that follow:
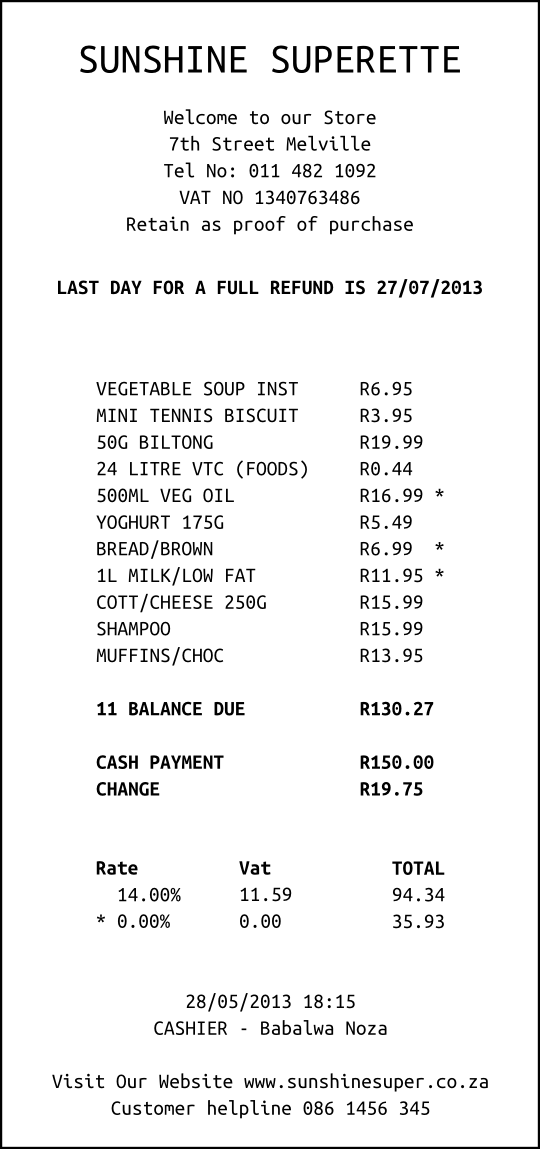
Boiketlo gave the cashier \(\text{R}\,\text{150,00}\) and received \(\text{R}\,\text{19,75}\) change.
Add together the total (including VAT) of the items that include VAT and the total of the VAT exempt items. Which letter (A, B, C or D) on the till slip does this correspond to?
Sakhile goes to his local department store and buys some clothes and groceries.
He receives the following till slip. Study the slip and answer the questions that follow:
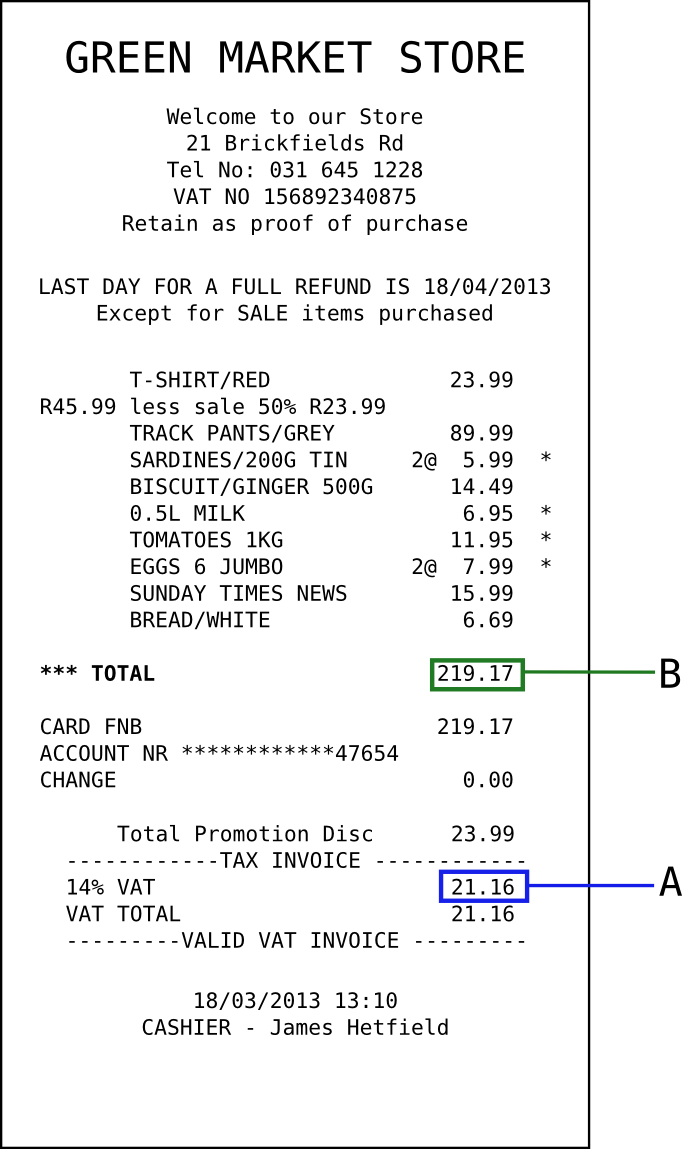
What item did Sakhile buy on sale, and how much was the discount?
A red T-shirt, \(\text{50}\%\) discount
Can Sakhile return the sale item for refund? Explain your answer.
No, full refunds are only available for non-sale items.
Sakhile finds a hole in the tracksuit pants that he bought.
Can he return them for a refund?
Yes - they were not sale items
If so, by what date must he return them?
Before or on 18 April 2013
How many eggs did Sakhile buy?
\(\text{2}\) packs of \(\text{6}\), so \(\text{12}\) eggs.
Calculate the total value of the VAT exempt items Sakhile bought.
\(\text{2}\)(\(\text{R}\,\text{5,99}\)) + \(\text{R}\,\text{6,95}\) + \(\text{11,95}\) + \(\text{2}\)(\(\text{R}\,\text{7,99}\)) = \(\text{R}\,\text{46,86}\)
Demonstrate how the amount indicated by Letter A was calculated. Show all your calculations.
VAT incl items total \(\text{R}\,\text{151,15}\). \(\text{14}\%\) VAT of this = \(\text{R}\,\text{21,16}\)
Demonstrate how the amount indicated by Letter B was calculated. Show all your calculations.

VAT incl items total \(\text{R}\,\text{151,15}\). \(\text{14}\%\) VAT on this = \(\text{R}\,\text{21,16}\). Non-VAT items total \(\text{R}\,\text{46,86}\). VAT incl + \(\text{14}\%\) + VAT excl = \(\text{R}\,\text{219,17}\).
At some clothing and food stores, it is possible to open an account, buy goods on credit and pay off what you owe the store on a monthly basis. Buying on credit basically means that you can take the items now and pay for them later. While this may seem like a good idea, it is all too easy to end up owing the shop more money you can pay them, which is a very bad position to be in. Many South Africans do have store accounts and manage them sensibly by paying back the shop each month, when they receive their monthly account statement.
In order to open a store account, you usually have to be 18 years or older, and be able to provide proof of employment and proof of residence. You are then issued with a store card (like a credit card but only for certain shops), and you receive monthly account statements detailing how much you've spent, how much you've paid back and how much you still owe the store.
Bulelwa has an Edgars store account. She receives the account statement below. Study the statement and answer the questions that follow:

Jane receives the following account statement from Woolworths. Answer the questions that follow.

Is there anything unusual about Jane's contact details, when compared to the bills we've worked with thus far?
Her contact details only list her e-mail address, no physical or postal address.
What is the opening balance on Jane's account?
\(\text{R}\,\text{4 318,33}\)
When last did she make a payment into her account and how much was it for?
Jane's last payment was for \(\text{R}\,\text{400}\), on 25 August 2013.
How many times did Jane shop at Woolworths in the month of August 2013?
\(\text{5}\) times
How much did she spend in total on goods from Woolworths in August 2013?
\(\text{R}\,\text{302,03}\) + \(\text{R}\,\text{171,74}\) + \(\text{R}\,\text{152,15}\) + \(\text{R}\,\text{279,67}\) + \(\text{R}\,\text{55,19}\) = \(\text{R}\,\text{960,78}\)
Which Woolworths store did she shop at the most often?
At Nichol Way, JHB
Jane lives in Johannesburg. Did she travel at all in the month of August 2013? Explain your answer.
Yes - on the 19th August she used her card at Cape Town Airport.
What is the minimum amount that Jane must pay into her account this month, and when must she pay it by?
\(\text{R}\,\text{371,21}\) must be paid by 7 October 2013.
How much credit does Jane have available?
\(\text{R}\,\text{251,00}\)
How much does she owe in total to Woolworths?
\(\text{R}\,\text{4 949,47}\)
Jane is interested in getting the credit card advertised at the bottom of the account statement. With this new credit card, if she spent \(\text{R}\,\text{400}\) at Woolworths, how much would money would she get back in WVouchers?
\(\text{3}\%\) of \(\text{R}\,\text{400}\) = \(\text{R}\,\text{400}\) \(\times \frac{\text{3}}{\text{100}}\) = \(\text{R}\,\text{400}\) \(\times\) \(\text{0,03}\) = \(\text{R}\,\text{12,00}\).
|
Previous
4.1 Introduction and key concepts
|
Table of Contents |
Next
4.3 Tariff systems
|