\(\text{5}\); \(\text{7}\); \(\text{19}\); \(\text{24}\); \(\text{10}\); \(\text{17}\); \(\text{21}\); \(\text{6}\); \(\text{22}\); \(\text{5}\); \(\text{9}\)
Mean = \(\text{13,18}\)
|
Previous
12.5 Classifying and organising data
|
Next
12.7 Representing data
|
After data has been collected, classified and organised it is not always possible to mention every piece of data in a report. Instead we summarise data by describing the whole data set using just a few numbers. Summarising data also makes it easier to analyse the data later.
Data can be summarised by using measures of central tendency or measures of spread.
Measure of central tendency is a single value that attempts to show what the central position is of a set of data. Measures of spread describe how the data is spread out or dispersed.
There are three types of measures of central tendency: mean, mode and median.
The mean is the most common measure of central tendency that is used. It is also known as the average. It is calculated by adding all the values together and dividing by the number of values in the data set. E.g. If you have numbers \(\text{2}\); \(\text{6}\); \(\text{8}\); \(\text{10}\); \(\text{12}\); \(\text{14}\); \(\text{18}\); the mean is calculated as:
\(\dfrac{\text{the sum of the observational values}}{\text{the number of observations}} = \dfrac{\text{2}\text{+6}\text{+8}\text{+10}\text{+12}\text{+14}\text{+18}}{ \text{7}} = \text{10}\)
Mark | \(\text{4}\) | \(\text{6}\) | \(\text{7}\) | \(\text{8}\) | \(\text{9}\) | \(\text{10}\) |
Frequency | \(\text{2}\) | \(\text{4}\) | \(\text{3}\) | \(\text{6}\) | \(\text{3}\) | \(\text{2}\) |

Find the mean of each of the following data sets:
\(\text{5}\); \(\text{7}\); \(\text{19}\); \(\text{24}\); \(\text{10}\); \(\text{17}\); \(\text{21}\); \(\text{6}\); \(\text{22}\); \(\text{5}\); \(\text{9}\)
Mean = \(\text{13,18}\)
\(\text{4}\); \(\text{3}\); \(\text{1}\); \(\text{6}\); \(\text{1}\); \(\text{3}\); \(\text{8}\); \(\text{2}\); \(\text{4}\); \(\text{3}\)
Mean =\(\text{3,5}\)
\(\text{24}\); \(\text{14}\); \(\text{41}\); \(\text{34}\); \(\text{26}\); \(\text{30}\); \(\text{25}\); \(\text{19}\); \(\text{27}\)
Mean =\(\text{26,67}\)
\(\text{190}\); \(\text{215}\); \(\text{187}\); \(\text{208}\); \(\text{212}\); \(\text{202}\)
Mean =\(\text{185,67}\)
The heights, in centimetres, of boys in the first soccer team are: \(\text{175}\); \(\text{168}\); \(\text{175}\); \(\text{176}\); \(\text{173}\); \(\text{168}\); \(\text{169}\); \(\text{176}\); \(\text{169}\); \(\text{191}\); \(\text{176}\). Find the mean height of these boys.

Mean = \(\text{174,18}\)
A short test was marked out of \(\text{10}\). The marks of \(\text{14}\) learners are: \(\text{4}\); \(\text{5}\); \(\text{6}\); \(\text{7}\); \(\text{8}\); \(\text{8}\); \(\text{6}\); \(\text{9}\); \(\text{9}\); \(\text{2}\); \(\text{10}\); \(\text{3}\); \(\text{5}\); \(\text{6}\). Find the mean mark for this test.
Mean = \(\text{6,29}\)
The frequency table below shows the amount of pocket money, to the nearest Rand that Grade 10 learners are given each week. Calculate the mean amount of pocket money per week.

Pocket money (nearest Rand) | \(\text{30}\) | \(\text{35}\) | \(\text{40}\) | \(\text{45}\) | \(\text{50}\) |
Frequency | \(\text{5}\) | \(\text{5}\) | \(\text{10}\) | \(\text{8}\) | \(\text{2}\) |
Mean =\(\text{R}\,\text{39,50}\)
For each set of data given in the frequency tables below, find the mean.
Time taken to complete class work (minutes) | \(\text{6}\) | \(\text{9}\) | \(\text{10}\) | \(\text{13}\) | \(\text{15}\) |
Frequency | \(\text{4}\) | \(\text{4}\) | \(\text{5}\) | \(\text{4}\) | \(\text{3}\) |
Mean = \(\text{10,35}\) minutes
Age of learners (in years) | \(\text{14}\) | \(\text{15}\) | \(\text{16}\) | \(\text{17}\) | \(\text{18}\) |
Frequency | \(\text{2}\) | \(\text{3}\) | \(\text{10}\) | \(\text{15}\) | \(\text{10}\) |
Mean = \(\text{16,7}\) years
When data is arranged in ascending order, it is arranged from the smallest value to the biggest value (e.g. \(\text{2}\); \(\text{3}\); \(\text{4}\); \(\text{5}\); \(\text{6}\)). When data is arranged in descending order, it is arranged from the biggest value to the smallest value (e.g. \(\text{6}\); \(\text{5}\); \(\text{4}\); \(\text{3}\); \(\text{2}\)). The middle value in the set of data values is called the median. E.g. If you have numbers \(\text{2}\); \(\text{3}\); \(\text{4}\); \(\text{5}\); \(\text{6}\); \(\text{7}\), and \(\text{8}\), the median is \(\text{5}\).
We need to consider two cases when we find the median of data:
Find the median of the numbers: \(\text{4}\); \(\text{6}\); \(\text{7}\); \(\text{4}\); \(\text{3}\); \(\text{4}\); \(\text{8}\); \(\text{2}\); \(\text{9}\); \(\text{7}\); \(\text{2}\).
First we must arrange the numbers in ascending order i.e.:
\(\text{2}\); \(\text{2}\); \(\text{3}\); \(\text{4}\); \(\text{4}\); \(\text{4}\); \(\text{6}\); \(\text{7}\); \(\text{7}\); \(\text{8}\); \(\text{9}\).
\(\text{2}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{4}\) | \(\text{4}\) | \(\text{6}\) | \(\text{7}\) | \(\text{7}\) | \(\text{8}\) | \(\text{9}\) |
\(\uparrow\) |
The arrow indicates the middle position. There are \(\text{5}\) numbers on each side of this number (\(\text{4}\)).
Therefore \(\text{4}\) is the median of the set of the numbers.
Find the median of the numbers: \(\text{4}\); \(\text{6}\); \(\text{4}\); \(\text{7}\); \(\text{2}\); \(\text{3}\); \(\text{8}\); \(\text{9}\); \(\text{7}\); \(\text{4}\)
First we must arrange the numbers in ascending order. i.e.:
\(\text{2}\); \(\text{3}\); \(\text{4}\); \(\text{4}\); \(\text{4}\); \(\text{6}\); \(\text{7}\); \(\text{7}\); \(\text{8}\); \(\text{9}\).
\(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{4}\) | \(\text{4}\) | \(\text{6}\) | \(\text{7}\) | \(\text{7}\) | \(\text{8}\) | \(\text{9}\) | |
\(\uparrow\) |
The arrow indicates the middle position. There is no number in this exact position. So we take the number that is halfway between \(\text{4}\) and \(\text{6}\).
Therefore the median \(=\frac{\text{4} + \text{6}}{\text{2}} = \text{5}\)
The mode is the data value that appears most often in a set of data. No calculation is needed to find or determine the mode. You just find the value that appears most frequently. E.g. If you have numbers \(\text{2}\); \(\text{5}\); \(\text{7}\); \(\text{7}\); \(\text{10}\); \(\text{12}\); \(\text{15}\), the mode is \(\text{7}\). If no number is repeated, then there is no mode for the list. You must also be aware that there can be more than one mode.
For grouped data, we use the modal class. This is the group or class that has the highest frequency.
The range is a measure of spread because it tells you how spread out the data values are. The range is found by finding the difference between the largest value and the smallest value.
Range =highest data value - lowest data value.
Find the range of the numbers \(\text{3}\); \(\text{7}\); \(\text{8}\); \(\text{5}\); \(\text{4}\); \(\text{10}\).
The lowest value is \(\text{3}\), and the highest is \(\text{10}\), so the range is \(\text{10}\) - \(\text{3}\) = \(\text{7}\).
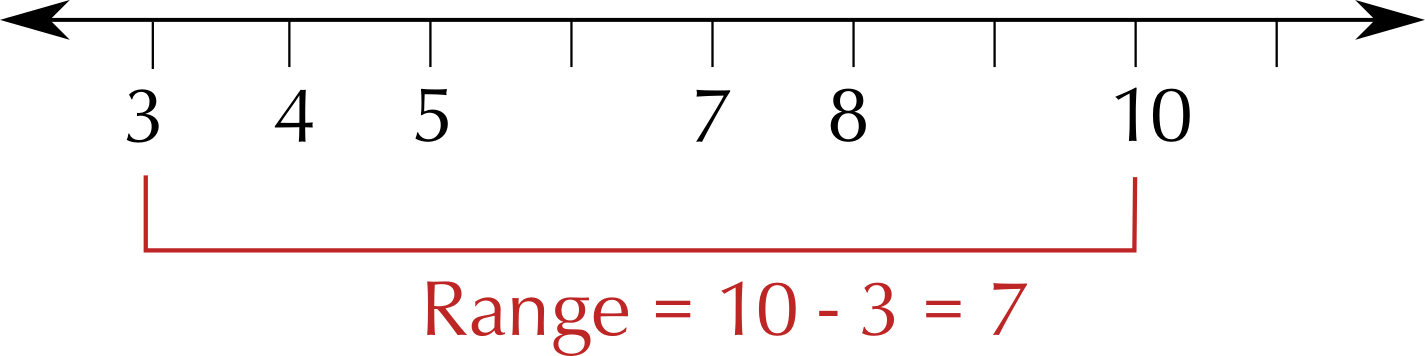
Note: It is important to remember to subtract the numbers and not leave the answer as \(\text{3}\) - \(\text{10}\) or \(\text{10}\) - \(\text{3}\).
Find the mean, mode, median and range for each of the following data sets:
\(\text{5}\); \(\text{7}\); \(\text{19}\); \(\text{24}\); \(\text{10}\); \(\text{17}\); \(\text{21}\); \(\text{6}\); \(\text{22}\); \(\text{5}\); \(\text{9}\)
Mean: \(\text{13,18}\). Mode: \(\text{5}\). Median: \(\text{10}\). Range: \(\text{24}\) - \(\text{5}\) = \(\text{19}\).
\(\text{190}\); \(\text{215}\); \(\text{187}\); \(\text{208}\); \(\text{212}\); \(\text{202}\)
Mean: \(\text{202,33}\). Mode: none. Median: \(\frac{\text{202} + \text{208}}{\text{2}}\) = \(\text{205}\). Range: \(\text{215}\) - \(\text{187}\) = \(\text{28}\).
The heights, in centimetres, of the girls in the cross-country running team are \(\text{175}\); \(\text{168}\); \(\text{175}\); \(\text{176}\); \(\text{173}\); \(\text{168}\); \(\text{169}\); \(\text{176}\); \(\text{169}\); \(\text{191}\); \(\text{176}\) \(\text{cm}\). Find the mean, mode, median and range of the height of these girls.

Mean: \(\text{174,18}\) \(\text{cm}\). Mode: \(\text{176}\) \(\text{cm}\). Median: \(\text{175}\) \(\text{cm}\). Range: \(\text{215}\) - \(\text{187}\) = \(\text{23}\) \(\text{cm}\).
Find the mean, median, mode and range of each of the following data sets:
\(\text{46}\); \(\text{32}\); \(\text{18}\); \(\text{6}\); \(\text{19}\); \(\text{32}\); \(\text{81}\); \(\text{24}\); \(\text{49}\); \(\text{33}\)
Mean: \(\text{34,1}\). Mode: \(\text{32}\). Median: \(\text{32}\). Range: \(\text{81}\) - \(\text{6}\) = \(\text{75}\).
\(\text{124}\); \(\text{214}\); \(\text{341}\); \(\text{134}\); \(\text{126}\); \(\text{130}\); \(\text{325}\); \(\text{319}\); \(\text{227}\)
Mean: \(\text{212,56}\). Mode: none. Median: \(\text{214}\). Range: \(\text{325}\) - \(\text{124}\) = \(\text{201}\).
Here is a list of the maximum temperatures for a week, in degrees Celsius:
\(\text{16}\); \(\text{3}\); \(\text{15}\); \(\text{25}\); \(\text{20}\); \(\text{19}\); \(\text{19}\)
Give the mean, median, mode and range of the temperatures.
Mean: \(\text{16,7}\). Mode: \(\text{19}\). Median: \(\text{19}\). Range: \(\text{25}\) - \(\text{3}\) = \(\text{22}\).
If the person who read the temperatures discovered that they had made a mistake and the \(\text{3}\) degrees was meant to be \(\text{23}\) degrees, how would this affect your summary of the data?
It would affect the mean and the range. The mode and median would still be \(\text{19}\), however.
|
Previous
12.5 Classifying and organising data
|
Table of Contents |
Next
12.7 Representing data
|