Does the advertisement indicate the percentage of interest that will be charged if the TV is not paid for in cash?
No.
|
Previous
11.2 Banking accounts and documents
|
Next
11.4 Value Added Tax
|
People need to pay interest when they borrow money, either from a bank, or if they purchase an item from a shop and pay it off in monthly installments using a hire purchase option. Buying an item on hire purchase is also borrowing money. The interest amount is calculated as a percentage of the amount owing.
If you save money in a bank account, you also earn interest on the balance in your account.

Interest rates can vary considerably. The interest rate that a person is charged depends on how much money they leave invested in the bank, and on other factors, including:
If we know what the interest rate is, we can calculate the interest value quite simply:
\(\text{10}\%\) interest on \(\text{R}\,\text{3 500}\) = \(\text{R}\,\text{3 500}\) \(\times\) \(\text{10}\%\) = \(\text{R}\,\text{350}\). So the interest amount is \(\text{R}\,\text{350}\) and the total amount is \(\text{R}\,\text{3 500}\) + \(\text{R}\,\text{350}\) = \(\text{R}\,\text{3 850}\).
If you are given the final amount, then you follow these steps to find the interest rate:
Let's look at a worked example to see how to do this.
Look at the advert below. You can buy a 3-piece wall unit cash for \(\text{R}\,\text{6 499,99}\). Alternatively, you could choose to buy it on hire purchase and pay for it in installments over \(\text{3}\) years. If you choose to pay it off in installments, you will pay interest every month on the wall unit.
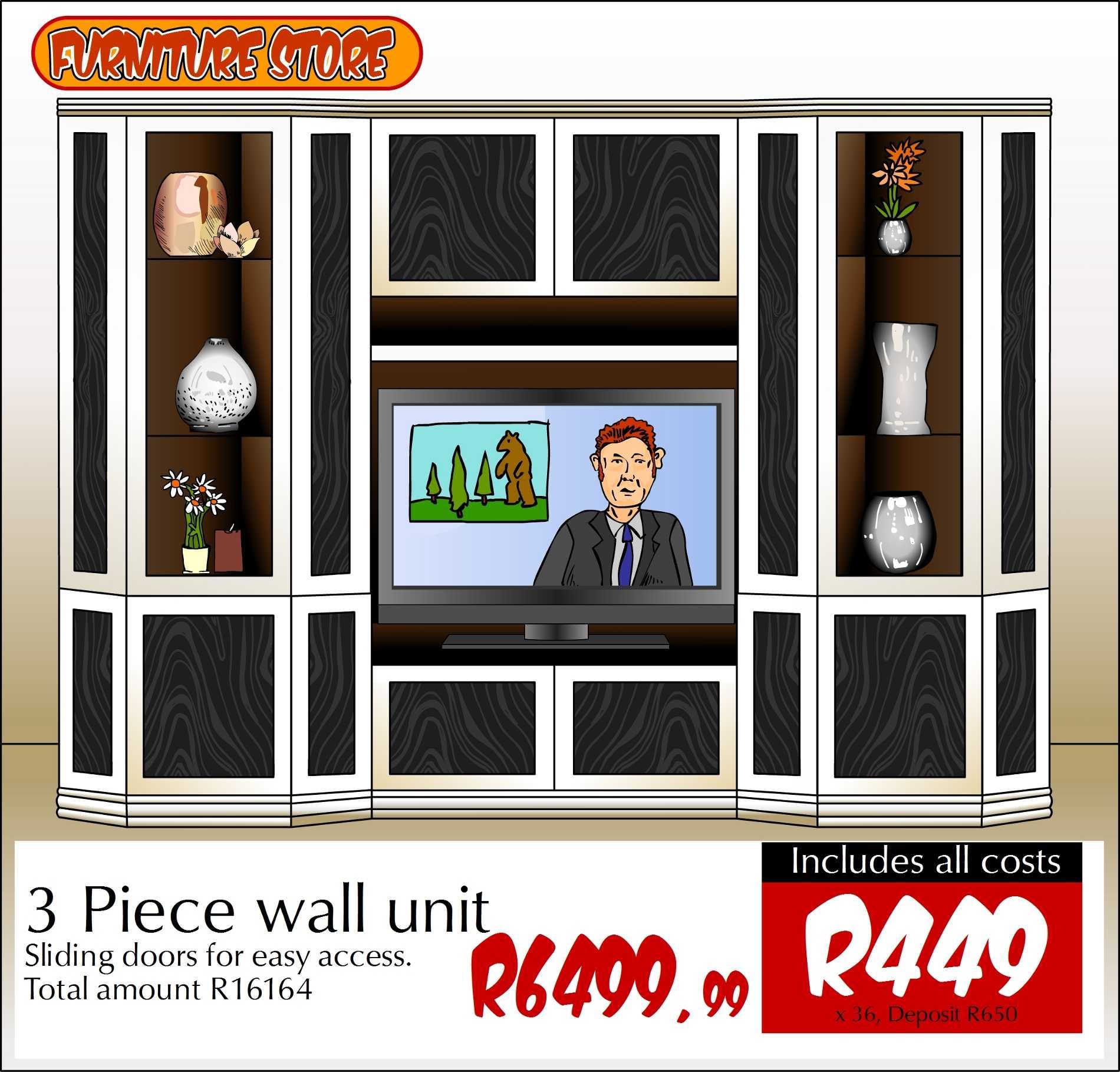
You found the following advertisement in a local newspaper. Answer the following questions.

Does the advertisement indicate the percentage of interest that will be charged if the TV is not paid for in cash?
No.
What will the balance be once the deposit has been paid?
Balance = Cash Price - Deposit = \(\text{R}\,\text{15 600}\) - \(\text{R}\,\text{1 560}\) = \(\text{R}\,\text{14 040}\)
Will the interest be charged on the full purchase price or on the balance?
It will be charged on the account balance.
How much will the installments be per month?
\(\text{R}\,\text{356,24}\)
How much will you have to pay for the TV in total? Use the formula: Total to be paid = Deposit + (Installment amount \(\times\) number of installments)
Total Payable = Deposit + (Installment amount \(\times\) number of installments) =\(\text{1 560}\) + (\(\text{356,24}\) \(\times\) [(\(\text{12}\) \(\times\) \(\text{5}\))]=\(\text{R}\,\text{1 560}\) + \(\text{R}\,\text{21 374,40}\) = \(\text{R}\,\text{22 934,40}\)
How much interest (in Rands) will you have paid once you have completed paying off the TV ? Use the formula: \(\frac{\text{Total interest payable}}{\text{Value}}\) = (Installment amount \(\times\) number of installments) \(-\) Balance
\(\frac{\text{Total interest payable}}{\text{Value}}\) = (Installment amount \(\times\) number of installments) \(-\) Balance = \(\text{R}\,\text{356,24}\) \(\times\) [ \(\text{12}\) \(\times\) \(\text{5}\) ] \(-\) \(\text{14 040}\) = \(\text{R}\,\text{21 374,40}\) \(-\) \(\text{R}\,\text{14 040}\) = \(\text{R}\,\text{7 334,40}\)
Grant borrows \(\text{R}\,\text{15 000}\) from his friend, Molefe, to finish an order for his customers. Molefe offers the following:
How much in total will Grant have to pay?

|
Previous
11.2 Banking accounts and documents
|
Table of Contents |
Next
11.4 Value Added Tax
|