• Construct and label the following triangles and quadrilaterals:
    1. Triangle FGH where GH = 6,2 cm; \(\hat{G}\) = 36\(^\circ\) and \(\hat{H}\) = 63\(^\circ\)
    2. Parallelogram PQRS where PQ = 5,7 cm, PS = 7,8 cm and \(\hat{R}\) = 112\(^\circ\)
    1. Construct \(\triangle\)KLM where KL = 9,4 cm; LM = 7 cm and MK = 7,8 cm.
    2. Construct the perpendicular bisectors of all three sides of the triangle drawn in part (a). You should find that they all go through the same point.
    3. Use the point of intersection as the midpoint of a circle that passes through all three vertices of the triangle. Use your compass to draw this circle.
  • Construct the following angles without using a protractor:
    1. 45\(^\circ\)
    2. 210\(^\circ\)
  • Construct a regular hexagon in your exercise books by following these instructions:
    • Construct a horizontal line, AB, which is 2 cm long.
    • Set your compass to 2 cm, and from each of A and B, draw an arc above line AB. Call the point that the arcs intersect O.
    • Draw a circle of radius 2 cm, centred on O. It should go through A and B.
    • Place the compass on point B, and draw an arc crossing the circle on the side opposite to A. Call this point C.
    • Repeat the above step to create points D to F.
    • Join B to C with a straight line. Repeat with C to D, and so on, until you get back to point A. You have now constructed a regular hexagon!
  • The following table summarises the properties of diagonals of quadrilaterals. Complete the table by placing ticks in the appropriate blocks.

    Parallelogram

    Rectangle

    Square

    Rhombus

    Trapezium

    Kite

    Diagonals bisect each other

    Diagonals cut at right angles

  • Study the following figure. Note that \(d\), \(e\) and \(f\) are the exterior angles of the triangle.

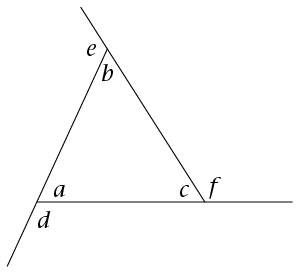
    86089.png

    1. Write down an equation that shows the relationship between angle d and the sum of two other angles in the image.
    2. Determine the size of d + e + f. Give reasons for your answer.
  • Determine the size of \(\hat{V}\). Show all steps of your working and give reasons when using any geometrical theorem:
    86072.png
  • DEFG is a square with DF = 12 cm. Determine the length of the side of the square, correct to two decimal places. Show all steps of your working. Give reasons when using any geometrical theorem:
    86053.png
  • Are the following pairs of triangles congruent? If they are, write down the relationship in the form \(\triangle\)XYZ \(\equiv\) \(\triangle\)ORQ, where X corresponds with O, Y with R, and so on. Also state the congruency condition (case) that proves the two triangles are congruent (for example, sss). If they are not congruent, explain why they are not congruent.

    Note: the triangles are not drawn to scale.

    1. 86043.png
    2. 86034.png
  • Provide a formal proof that the two triangles in the diagram below are congruent:
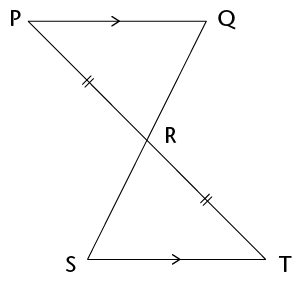
    86024.png
  • Study the diagram alongside:
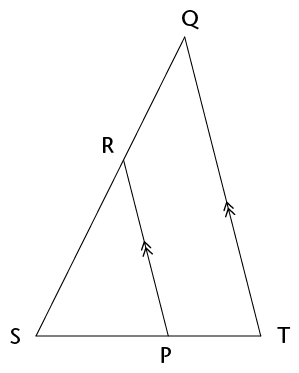
    85996.png

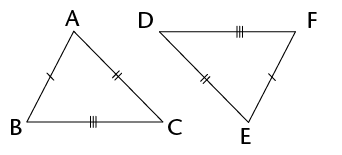
    Prove that \(\triangle\)SRP \(|||\) \(\triangle\)SQT.

  • Determine the size of \(P\hat{M}Q\).
    85939.png
  • Determine the size of \(x\) in each case. Show all steps of your working and give reasons when using any geometrical theorem:
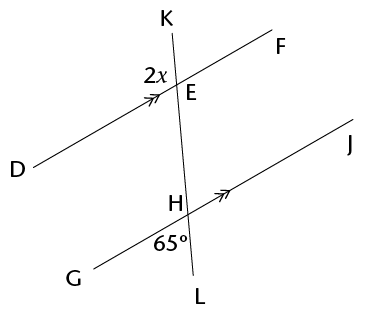
    1. 85915.png
    2. Given: EH = EJ
      85904.png
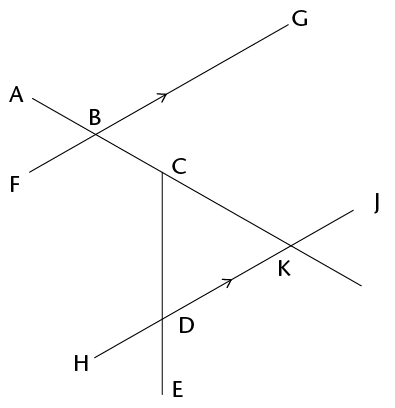
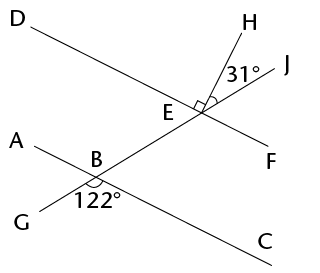
    3. \(A\hat{B}G = x\); \(B\hat{C}D = 130^\circ\) and \(C\hat{D}J = 72^\circ\)
      85870.png
    4. 85862.png
  • For which value of \(x\) are AB and CD parallel? Show all steps of your working and give reasons when using any geometrical theorem.
    85853.png
  • Calculate the missing side length in each of the following triangles:
    1. 85837.png
    2. 85845.png
  • A river is 50 m wide. Assume that the river flows completely straight. If Camelia swims across the river to a point on the bank 12 m downstream from the point directly opposite her, how far will she swim? Give your answer correct to one decimal place.
  • Triangle LMN is isosceles, with LM = LN. MN = 36 cm and LP = 24 cm. Determine the perimeter of the triangle.

    85623.png

  • DEFG is a rectangle, with DE = 20 cm and diagonal EG = 101 cm. Determine the area of the rectangle.
  • Is it possible to have a right-angled triangle with the following side lengths: 36; 76 and 84? Show all working necessary to support your answer.
  • Determine (i) the perimeter, and (ii) the area, of each of the following shapes. If necessary, give your answers in centimetres or square centimetres, correct to one decimal place:
    1. BF = 8 cm; BC = 10 cm; FD = 6 cm
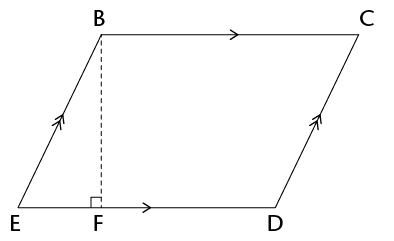
      85597.png
    2. GI = 12 cm; JK = 6 cm and JK : KH = 1 : 2
      85586.png
    3. The shape alongside is that of a window, consisting of a rectangular section HJKL, and a semi-circular top section. HJ = 0,5 m and JK = 0,2 m.
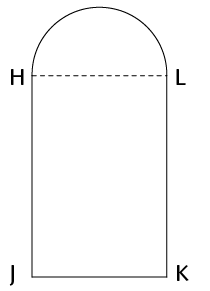
      85578.png
  • A button is made in the shape of a circle, with two congruent rectangles cut out, as shown in the diagram. The diameter of the button is 25 mm and the dimensions of each rectangle are 12 mm by 3 mm. Calculate the area of the top surface of the button in square centimetres.
    85570.png
  • A rectangle has length \(3d\) and width \(7e\). Write simplified expressions for the:
    1. Area of the rectangle
    2. Perimeter of the rectangle
  • Complete the unshaded blocks in following table to show the impact on the perimeter and area of doubling one dimension of the shape (for a rectangle, the length; for a triangle, the base; and for a circle, the radius). Assume that the original perimeter was \(x\), and the original area was \(y\). One answer has already been added for you.

    Rectangle

    Triangle

    Circle

    New perimeter/circumference

    New area

    		 \(2y\)
    1. Construct a triangle RST with RS = 7,3 cm, \(\hat{R}\) = 42\(^\circ\); and \(\hat{S}\) = 67\(^\circ\). (

      Use a protractor and ruler to check that the learners' constructions are accurate. Allow an error of up to 1 mm and 1\(^\circ\).

    2. Construct the bisectors of each of the angles of the triangle that you constructed in part (a). You should find that they have a common point of intersection.
    3. Use the common point of intersection of the bisectors of the angles that you constructed in part (b) as the midpoint of a circle touching all three sides of the triangle. Use your compass to draw this circle.
    4. Is it always possible to draw a triangle given the length of one of the lines and the sizes of the angles adjacent to that line (as was given in part (a), for example)? Explain your answer.
    5. Construct the following angle without using a protractor: 150\(^\circ\).
    6. Mthunzi is thinking of a quadrilateral and provides the following clue to Sam: "Its diagonals cut perpendicularly, but not all the sides of the shape are equal in length." Help Sam by writing down the special name of the shape.
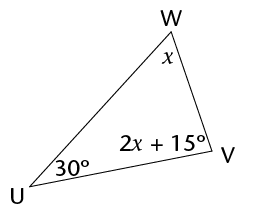
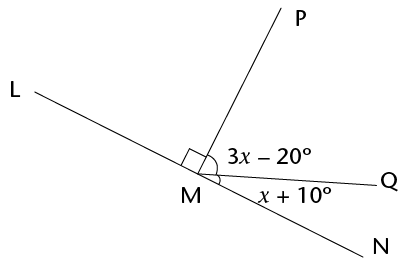
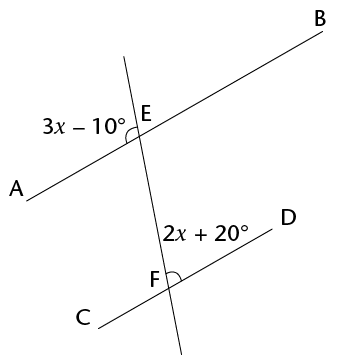
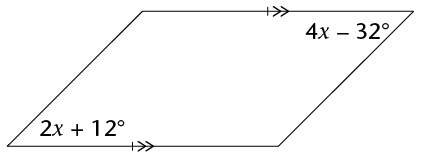
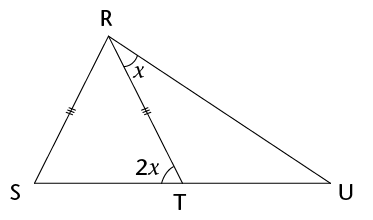
    7. Look at the figure below. Write down an equation, and use it to determine the size of x. (3)

      85534.png

  • Study the diagram alongside:
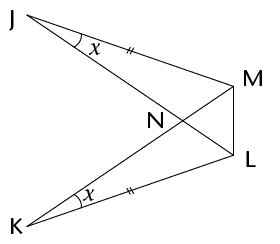
    85522.png
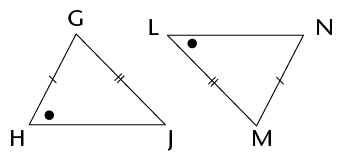
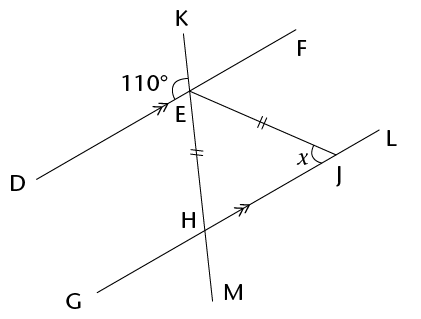
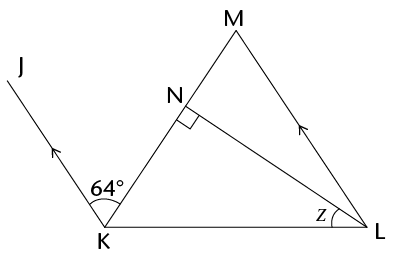
    1. Prove that \(\triangle\)JNM \(\equiv\) \(\triangle\)KNL.
    2. Do you have enough information to prove that \(\triangle\)JLM \(\equiv\) \(\triangle\)KML? Explain your answer.
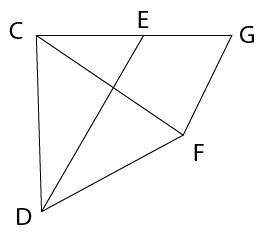
    3. Study the diagram alongside:

      Given that \(\triangle\)CDE \(\equiv\) \(\triangle\)FCG, prove that ED \(||\) GF. Give reasons for all statements.

      85480.png
  • Study the diagram below. All numerical values represent lengths of sides:

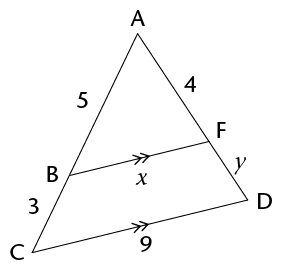
    85457.png

    1. Briefly explain why \(\triangle\)ABF \(|||\) \(\triangle\)ACD (a full proof is NOT required).
    2. Use the similarity of the triangles to determine the lengths of the line segments (correct to one decimal place).
      1. \(x\)
      2. \(y\)
  • Study the diagram alongside. Determine, with reasons, the size of \(\hat{U}\) in terms of \(x\).
    85440.png
  • Study the diagram alongside. Given that MK = ML, determine, with reasons, the value of z.
    85413.png
  • Is AC \(||\) DF? Explain your answer by means of a proof.
    85403.png
  • Study the diagram alongside. QRST is a rectangle. All numerical values represent lengths:
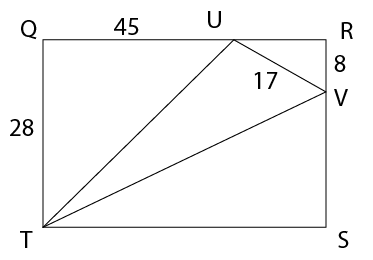
    85390.png
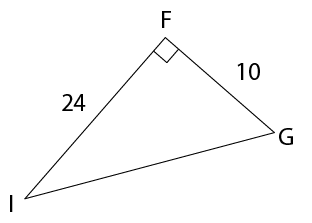
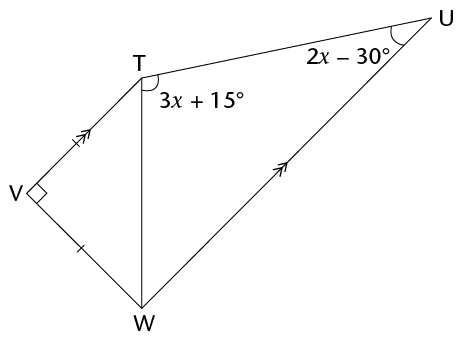
    1. Calculate the length of UT.
    2. Calculate the perimeter of triangle TUV, correct to one decimal place.
  • A rectangle has an area of \(6a^{2}\) and a perimeter of \(10a\). Determine, in terms of \(a\), the dimensions of the rectangle.
  • On the grid below, draw a parallelogram that has the same area as the triangle.
    85359.png
  • The perimeter of a rhombus is 60 cm, and the length of one of its diagonals is 24 cm.
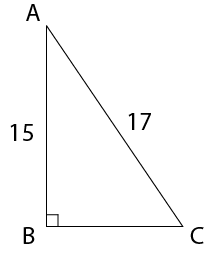
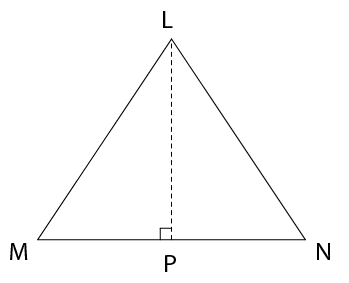
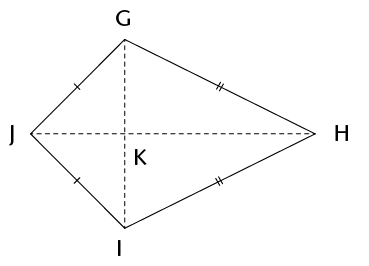
    1. Calculate the length of a side of the rhombus.
    2. Show that the area of the rhombus is 216 cm2.