Pythagoras (569-475 BC)
Pythagoras was an influential mathematician. like many Greek mathematicians of 2500 years ago, he was also a philosopher and a scientist. He formulated the best known theorem, today known as Pythagoras' Theorem. However, the theorem had already been in use 1000 years earlier, by the Chinese and Babylonians.
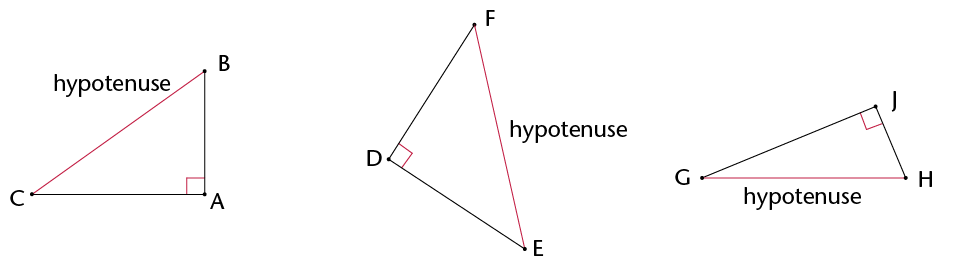
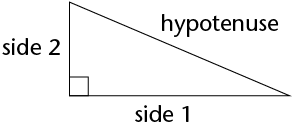
The hypotenuse is the side opposite the 90\(^\circ\) angle in a right-angled triangle. It is always the longest side.
How to say it:
'high - pot - eh - news'
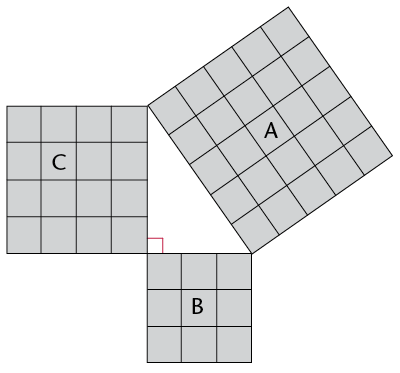
- Write down the areas of
the following:
Square A:
Square B:
Square C:
- Add Area of square B + Area of square
C:
- What do you notice about the areas?
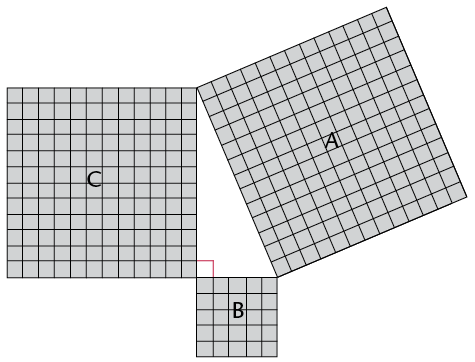
- What is the length of the hypotenuse?
Count the squares.
- Use the squares to find the
following:
Area of A:
Area of B:
Area of C:
Area of B + Area of C:
- What do you notice about the areas? Is
it similar to your answer in 1(c)?
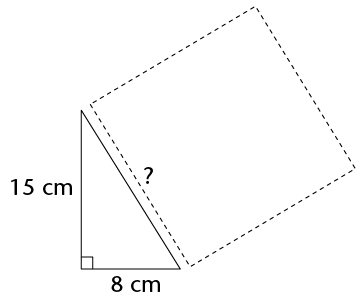
- What is the area of the square drawn
along the hypotenuse?
- What is the length of the triangle's
hypotenuse?
In the previous activity, you should have discovered Pythagoras' Theorem for right-angled triangles.
Pythagoras' Theorem says:
In a right-angled triangle, a square formed on the hypotenuse will have the same area as the sum of the area of the two squares formed on the other sides of the triangle. Therefore:
\((\text{Hypotenuse})^2 = (\text{Side 1} )^2 + (\text{Side 2})^2\)

- 7, 9 and 12
- 7, 12 and 14
- 16, 8 and 10
- 6, 8 and 10
- 8, 15 and 17
- 16, 21 and 25
 surd.
surd.Surd form
You pronounce surd so that it rhymes with word.
\(\sqrt{5}\) is an example of a number in surd form.
\(\sqrt{9}\) is not a surd because you can simplify it:
\(\sqrt{9}\) = 3
Example: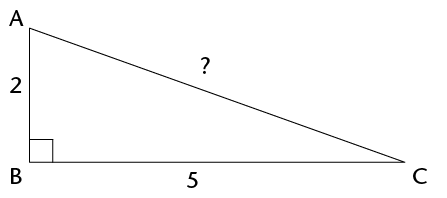
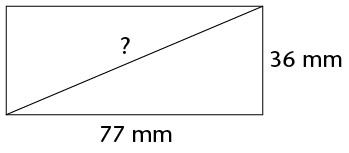
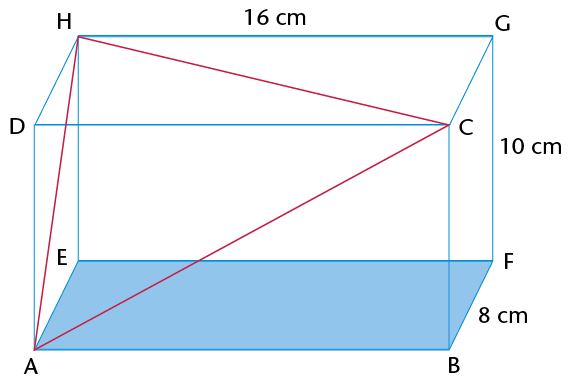
- Calculate the length of the sides of
\(\triangle\)ACH. Note that all three sides of the triangles are
diagonals of rectangles. AC is in rectangle ABCD, AH is in ADHE
and HC is in HDCG.
- Is \(\triangle\)ACH right-angled? Explain
your answer.
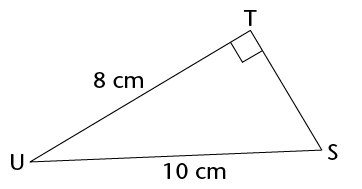
- \(\triangle\)ABC has AB = 12 cm, BC = 18 cm
and \(\hat{A}\) = 90\(^\circ\). Calculate AC.
- \(\triangle\)DEF has \(\hat{F}\)= 90\(^\circ\), DE = 58 cm and DF = 41
cm. Calculate EF.
- \(\triangle\)JKL has \(\hat{K}\) = 90\(^\circ\), JK = 119 m, KL = 167 m.
Calculate JL.
- \(\triangle\)PQR has PQ = 2 cm, QR
= 8 cm and \(\hat{Q}\) = 90\(^\circ\). Calculate PR.
- A ladder of length 5 m is placed at
an angle against a wall. The bottom of the ladder is 1 m away
from the wall. How far up the wall will the ladder reach? Round
off to two decimal places.
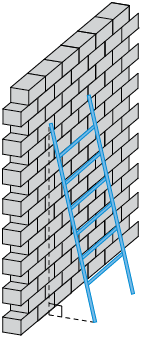
- If the ladder reaches a height of 4,5 m
against the wall, how far away from the wall was it placed?
Round off to two decimal places.
Sets of whole numbers that can be used as the sides of a right-angled triangle are known as Pythagorean triples, for example:
3-4-5 ;5-12-13 ;7-24-25 ;16-30-34 ;20-21-29
You extend these triples by finding multiples of them. For examples, triples from the 3-4-5 set include the following:
3-4-5 ;6-8-10 ;9-12-15 ;12-16-20
There are many old writings that record Pythagorean triples. For example, from 1900 to 1600 BC the Babylonians had already calculated very large Pythagorean triples, such as:
1 679-2 400-2 929.
How many Pythagorean triples can you find? What is the largest one you can find that is not a multiple of another one?
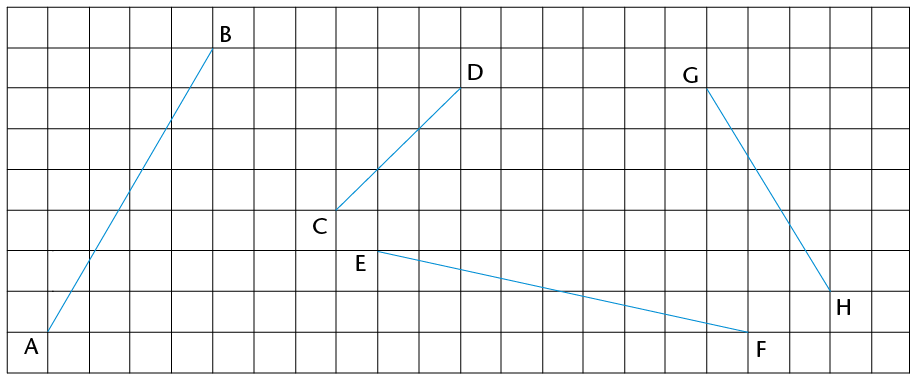
- Calculate the area of rectangle
KLMN.
- Calculate the perimeter of
\(\triangle\)KLM.
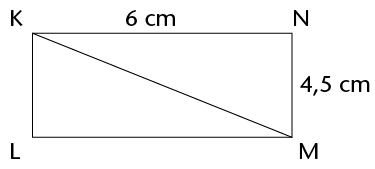
- What is the length of QD?
- If CP = 4,2 cm, calculate the length of
PQ.
- Calculate the length of AQ and the area
of \(\triangle\)AQD.
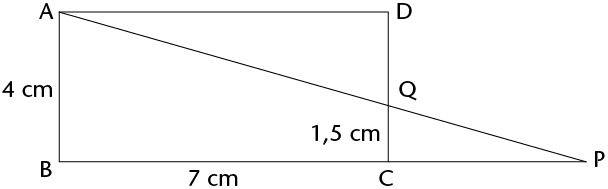
- Calculate the area of \(\triangle\)MNR.
- Calculate the perimeter of MNST.
Pythagoras' Theorem works only for right-angled triangles. But we can also use it to find out whether other triangles are acute or obtuse, as follows.
- If the square of the longest side is less than the sum of the squares of the two shorter sides, the biggest angle is acute .
For example, in a 6-8-9 triangle: \(6^{2}\) + \(8^{2}\) = 100 and \(9^{2}\) = 81.
81 is less than 100 \(\therefore\) the 6-8-9 triangle is acute.
- If the square of the longest side is more than the sum of the squares of the two shorter sides, the biggest angle is obtuse .
For example, in a 6-8-11 triangle: \(6^{2}\) + \(8^{2}\) = 100 and \(11^{2}\) = 121.
121 is more than 100 \(\therefore\) the 6-8-11 triangle is obtuse.
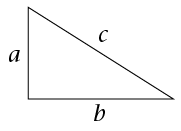
Complete the following table. It is based on the triangle on the right. Decide whether each triangle described is right-angled, acute or obtuse.
|
\(a\) |
\(b\) |
\(c\) |
\(a^{2} + b^{2}\) |
\(c^{2}\) |
Fill ini =, > or < |
Type of triangle |
|
3 |
5 |
6 |
\(3^{2} + 5^{2} = 9 + 25 = 34\) |
\(6^{2}\) = 36 |
\(a^{2} + b^{2} \gt c^{2}\) |
Acute |
|
2 |
4 |
6 |
\(a^{2} + b^{2}\) ........... \(c^{2}\) |
|||
|
5 |
7 |
9 |
\(a^{2} + b^{2}\) ........... \(c^{2}\) |
|||
|
12 |
5 |
13 |
\(a^{2} + b^{2}\) ........... \(c^{2}\) |
|||
|
12 |
16 |
20 |
\(12^{2} + 16^{2} = 144 + 256 = 400\) |
\(20^{2} = 400\) |
\(a^{2} + b^{2}\) ........... \(c^{2}\) |
Right-angled |
|
7 |
9 |
11 |
\(\text{a}^{2}\) + \(\text{b}^{2}\) ........... \(\text{c}^{2}\) |
|||
|
8 |
12 |
13 |
\(\text{a}^{2}\) + \(\text{b}^{2}\) ........... \(\text{c}^{2}\) |
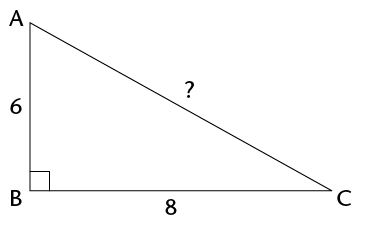
- Write down Pythagoras' Theorem in the way that
you best understand it.
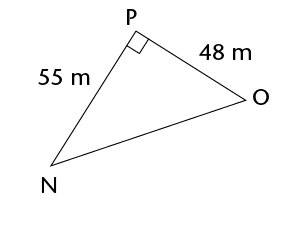
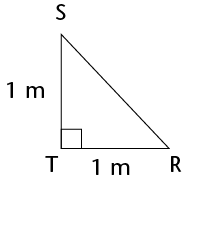
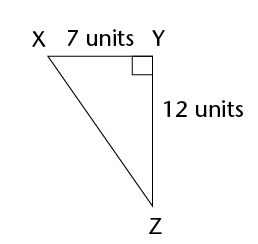
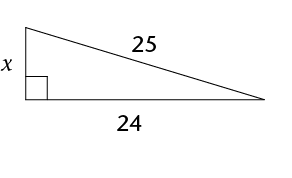
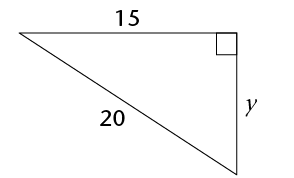
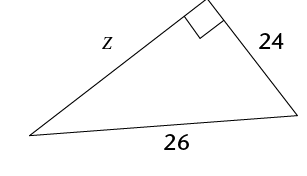
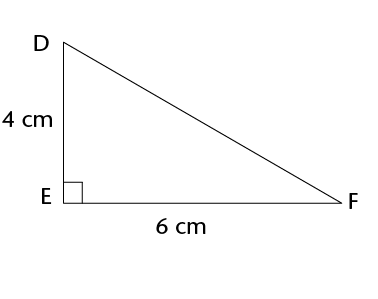
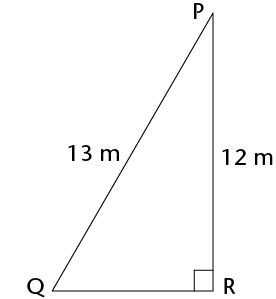
- Calculate the lengths of the
missing sides in the following triangles. Leave the answers in
surd form if necessary.
-
- ABCD is a parallelogram.
- Calculate the perimeter of
ABCD.
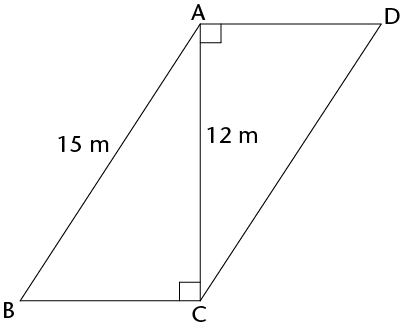
- Calculate the area of ABCD.
- Calculate the perimeter of
ABCD.