You are going to choose a number, multiply it by 5, and subtract the answer from 50.
-
Choose any number from set A and do the above calculations.
-
Choose any number from set B and do the above calculations.
-
If you choose any other number from set B, do you think the answer will also be a negative number?
-
Write down all the different output numbers that will be obtained when the calculations \(50 - 5x\) are performed on the different numbers in set A.
Output numbers are numbers that you obtain when you apply the rule to the input numbers.
-
Write down the output numbers that will be obtained when the formula \( 50 - 5x\) is applied to set B.
-
Complete the following table for set A:
Input numbers
1
2
3
4
5
6
7
8
9
Values of \( 50 - 5x\)
-
Complete the following table for set B:
Input numbers
20
30
40
50
60
70
80
90
Values of \(50 - 5x\)
In this question your set of input numbers will be the even numbers 2; 4; 6; 8; 10; ...
-
What will all the output numbers be if the rule \(2n + 1\) is applied to the set of even numbers? Write a list.
-
What will the output numbers be if the rule \(2n- 1 \)is applied?
-
What will the output numbers be if the rule \(2n + 5\) is applied?
-
What will the output numbers be if the rule \(3n + 1\) is applied?
-
What kind of output numbers will be obtained by applying the rule \(x - 1 000\) to natural numbers smaller than 1 000?
-
What kind of output numbers will be obtained by applying the rule \(\frac{x}{10} + 10\) to natural numbers smaller than 10?
-
If you use the rule \( 30x + 2\), and use input numbers that are positive fractions with denominators 2, 3 and 5, what kind of output numbers will you obtain?
A quantity that changes is called a variable quantity or just a variable.
If one variable quantity is influenced by another, we say there is a relationship between the two variables. You can sometimes work out which number is linked to a specific value of the other variable.
The output number can also be called the output value, or the value of the expression, which is \(10x + 5\) in this case.
Arelationship between two variables in which there is only one output number for each input number, is called a function.
- With a table that shows some values of the two variables. A table shows clearly which value of the output variable corresponds to each particular value of the input variable.
- A flow diagram, which shows what calculations are to be done to calculate the output number that corresponds to a given input variable.
- A formula, which also describes what calculations are to be done to calculate the output number that corresponds to a given input variable.
- A graph.
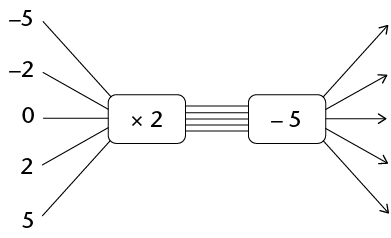
Complete the flow diagram:
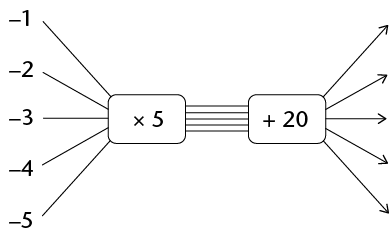
A completed flow diagram shows two kinds of information:
- It shows what calculations are done to produce the output numbers.
- It shows which output number is connected to which input number.
The output numbers of a function are also called function values. Hence the formula can also be written as
function value = \(5x + 20\)
Complete this table for the function described by \(5x + 20\):
|
Input numbers |
-1 |
-2 |
-3 |
-4 |
-5 |
|
Function values |
Draw a graph of this function below.

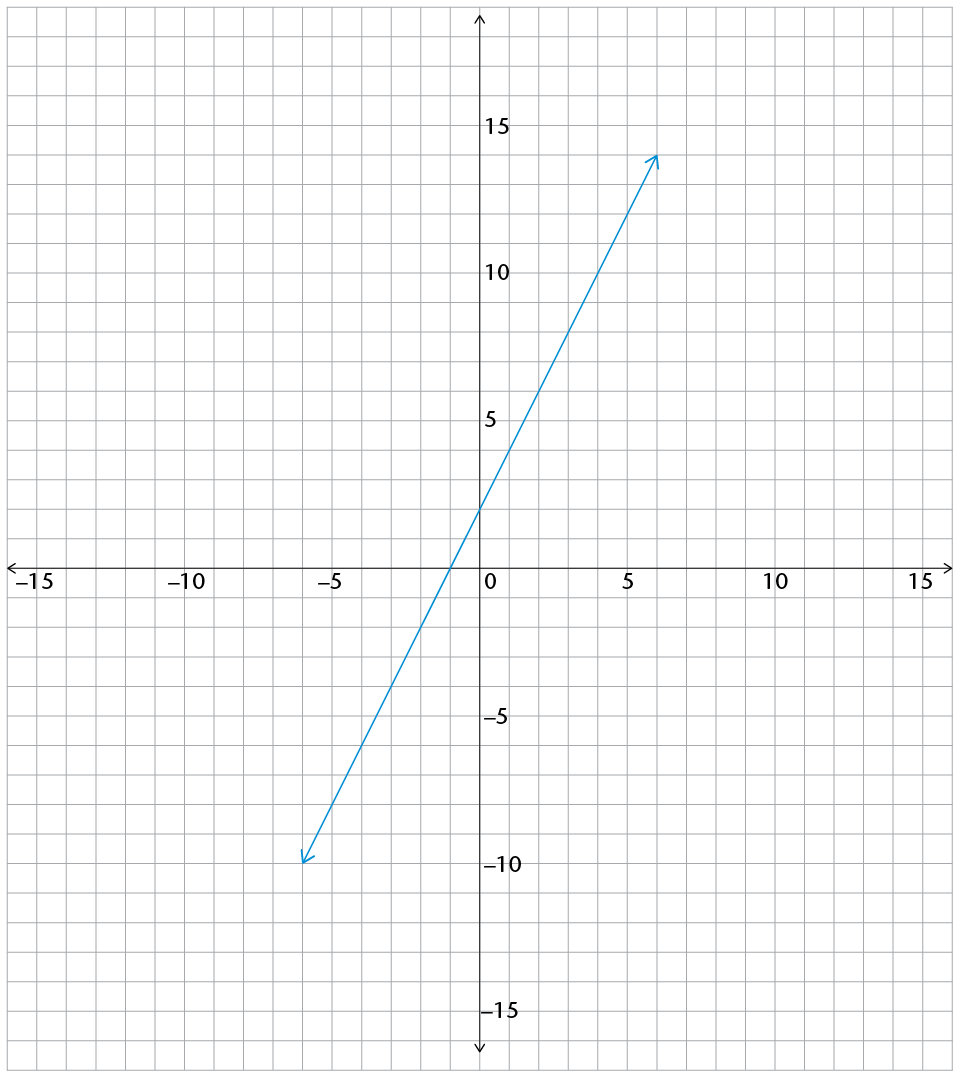
A graph of a certain function is given below. Complete the table for this function.
|
Input numbers |
|||||
|
Function values |
a flow diagram
a table of values for the set of integers from -5 to 5
a graph
The relationship described by the expression \(3x + 4\)
The relationship described by the expression \( 2x - 5\)
The relationship described by the expression \(\frac{1}{2}x +2\)
The relationship described by the expression \(-3x + 4\)
The relationship described by the expression \(2,5x + 1,5\)
The relationship described by the expression \(0,2x + 1,4\)
The relationship described by the expression \( -2x-4\)