17.2 Revision: Surface area, volume and capacity
Surface area is the total area of the exposed or outer surfaces of an object.
- surface area
- the total area of the exposed or outer surfaces of an object
Imagine an object made from cardboard that we can cut and unfold so that it lies flat on a surface. A solid that is unfolded like this is called a net. When a cuboid is unfolded into a net, we can clearly see its six rectangular faces.
- net
- a flat diagram that can be folded to form a three-dimensional shape
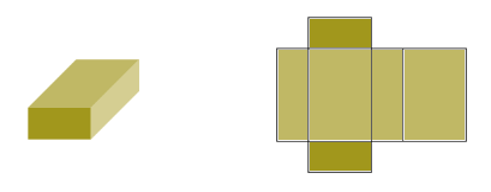
In order to calculate the surface area of the rectangular prism, we calculate the area of each rectangle, and add all the areas together. Surface area is measured in square units.
Volume is the amount of space that a three-dimensional (3D) object takes up. Volume is measured in cubic units.
- volume
- the amount of space that a three-dimensional (3D) object takes up
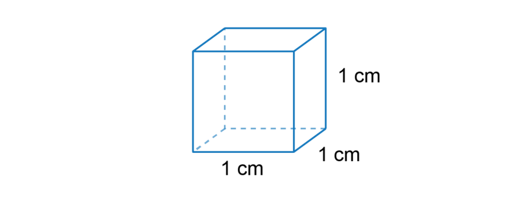
Therefore, when we measure volume, we measure three dimensions. The cube below has a length of \(1 \text{ cm}\), a breadth of \(1 \text{ cm}\) and a height of \(1 \text{ cm}\). The volume of the cube is \(1 \text{ cm}^3\). We say the volume is “\(1\) cubic centimetre”.
The capacity of an object is the amount of substance it can hold if it is filled to its maximum. We often use the term to refer to liquid measurements. Capacity can be expressed in millilitres (\(\text{ml}\)) and litres (\(\text{l}\)).
- capacity
- the maximum amount that a container can hold
The following conversions are useful to remember when working with volume and capacity:
- \(1 \text{ cm} = 10 \text{ mm}\)
- \(1 \text{ cm}^3 = 10 \text{ mm} \times 10 \text{ mm} \times 10 \text{ mm} = 1\ 000 \text{ mm}^3\)
- \(1 \text{ ml} = 1 \text{ cm}^3\)
- \(1 \text{ litre} = 1\ 000 \text{ ml} = 1\ 000 \text{ cm}^3\)
- \(1 \text{ kl} = 1 \text{ m}^3\)
An object with a volume of \(1 \text{ cm}^3\) will displace \(1 \text{ ml}\) of water. An object with a volume of \(1 \text{ m}^3\) will displace \(1 \text{ kl}\) of water.
Take note that capacity and volume are not the same. The capacity of this glass is \(300 \text{ ml}\), but the volume of orange juice in the glass is \(50 \text{ ml}\).
