13.6 Chapter summary
- Instead of writing \(2\) fifths, we may write \(\frac{2}{5}\). This is called the common fraction notation. The number \(5\) below the line is called the denominator. The number \(2\) above the line is called the numerator.
- \(\frac{3}{4}\), \(\frac{6}{8}\), \(\frac{15}{20}\), \(\frac{45}{60}\) are all different ways of expressing the same number. They are therefore called equivalent fractions.
- Proper fractions are fractions that are less than one; the numerator is always less than the denominator.
- Improper fractions are fractions that are greater than or equal to one; the numerator is larger than or equal to the denominator.
- Mixed numbers (mixed fractions) are numbers that have an integer part and a fraction part; the fraction part must be a proper fraction (less than one).
- When you simplify a fraction, you must reduce the numbers in the fraction to the smallest possible values. We do this by cancelling the highest common factor from the numerator and the denominator.
- To convert a mixed number to an improper fraction, start at the denominator; then follow the solid arrow around and multiply by the integer in the front; then continue following the dashed arrow and add the numerator. Keep the same denominator:
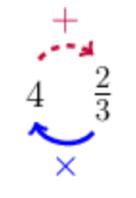
- To convert an improper fraction to a mixed number, divide the numerator by the denominator (change the fraction to a division problem).
Start by finding out how many times \(2\) fits into \(5\). \(2 \times 2 = 4\), which leaves \(1\) as a remainder. Keep the denominator the same.
\[\begin{align} \frac{5}{2} = 2\frac{1}{2} \end{align}\]- To add (or subtract) fractions:
- Make sure that they have the same denominators. Convert the fractions to equivalent fractions that have the same denominators using the lowest common denominator (LCD), if necessary.
- Add (or subtract) the numerators.
- To multiply fractions:
- Cross cancel any common factors. (This is not strictly necessary, but it will make your life easier.)
- Multiply the numerators, and multiply the denominators.
- Multiplying fractions follows this rule:
- To divide fractions:
- “Tip and times”: multiply by the reciprocal of the fraction in the divisor (the second fraction).
- Multiply the fractions as normal.
- Dividing fractions follows this rule, which uses the reciprocal of the second fraction:
- Remember that per cent means per hundred. For example, \(\frac{2}{10} = \frac{20}{100}\) which is \(20\) per hundred \(= 20\%\). To convert a fraction to a percentage, find the equivalent fraction with the denominator \(100\). The numerator of the new fraction shows you the amount per hundred, or per cent.
- To calculate the percentage increase or decrease:
Calculate the difference between the two amounts.
- If it is a percentage increase, then subtract the original amount from the new amount.
- If it is a percentage decrease, then subtract the final amount from the new amount.
