- \(23^{\circ}\)
- \(58^{\circ}\)
- \(14^{\circ}\)
- \(65^{\circ}\)
- \(79^{\circ}\)
- \(36^{\circ}\)
- \(67^{\circ}\)
- \(32^{\circ}\)
- \(76^{\circ}\)
- \(25^{\circ}\)
- \(11^{\circ}\)
- \(54^{\circ}\)
|
Previous
Constructing angles
|
Next
Constructing triangles
|
In this section, you will learn how to construct \(30^{\circ}\), \(45^{\circ}\) and \(60^{\circ}\) angles using a compass. You will also learn how to construct multiples or combinations of these angles.
When the sum of two angles is equal to \(90^{\circ}\), we say that the two angles are complementary angles.
For example:
When the sum of two angles is equal to \(180^{\circ}\), we say that the two angles are supplementary angles.
For example:
\(\hat{T}\) and \(\hat{S}\) are complementary angles. If \(\hat{S} = 37^{\circ}\), determine \(\hat{T}\).
We know that complementary angles are two angles that together have a sum of \(90^{\circ}\).
So:
\[\begin{align} \hat{T} + \hat{S} &= 90^{\circ} \\ \hat{T} &= 90^{\circ} − \hat{S} \\ \hat{T} &= 90^{\circ} − 37^{\circ} \\ \therefore \hat{T} &= 53^{\circ} \end{align}\]\(\hat{P}\) and \(\hat{Q}\) are supplementary angles. Find the value of \(\hat{Q}\) if \(\hat{P} = 106^{\circ}\).
The sum of supplementary angles is equal to \(180^{\circ}\).
So:
\[\begin{align} \hat{P} + \hat{Q} &= 180^{\circ} \\ \hat{Q} &= 180^{\circ} − \hat{P} \\ \hat{Q} &= 180^{\circ} − 106^{\circ} \\ \therefore \hat{Q} &= 74^{\circ} \end{align}\]\(\hat{P}\) and \(\hat{Q}\) are complementary angles. If \(\hat{P} = 35^{\circ}\), find the size of \(\hat{Q}\).
\(\hat{R}\) and \(\hat{S}\) are supplementary angles. If \(\hat{R} = x\) and \(\hat{S} = 4x\), find the size of \(\hat{R}\) and \(\hat{S}\).
\(\hat{R} = 36^{\circ}\) and \(\hat{S} = 144^{\circ}\)
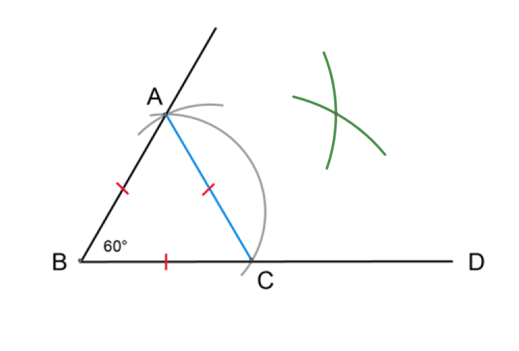
Use a compass to construct a \(60^{\circ}\) angle.
Use a ruler to draw a line segment \(BD\). This line segment will form one of the arms of the angle.

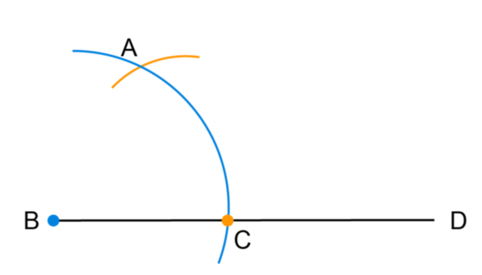
Place the point of the compass on point \(B\) and construct a wide arc as shown in the diagram below. The point where the arc intersects the line \(BD\) is labelled \(C\).

Without changing the width of the compass, place the compass on point \(C\) and construct a second arc that intersects the first arc. The point where the two arcs intersect is labelled point \(A\).
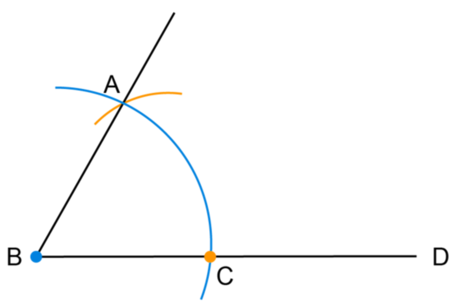
Use a ruler to draw the line segment \(BA\) which forms the other arm of the angle.
\(A\hat{B}C = 60^{\circ}\). We can use a protractor to check the accuracy of the construction.
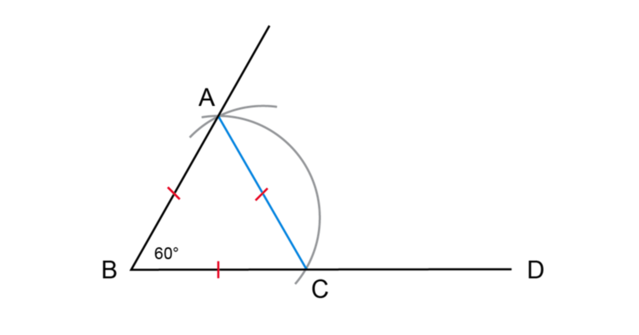
In the previous worked example, we constructed a \(60^{\circ}\) angle. Look at the steps of the construction. Did you notice that \(BC = CA = AB\)? The diagram below shows the final step of the same construction with line segment \(CA\) drawn. This means that we have constructed an equilateral triangle with all sides equal in length.
\(\triangle ABC\) is an equilateral triangle with \(BC = CA = AB\).
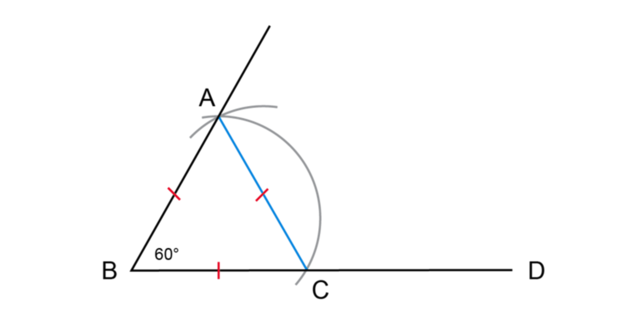
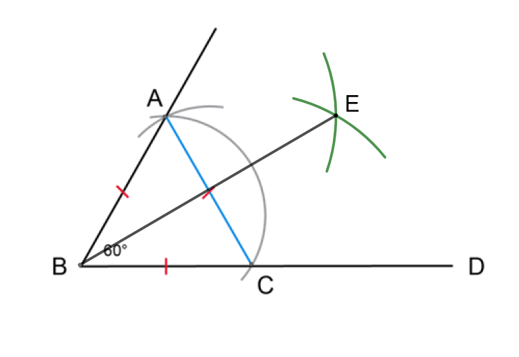
To construct a \(30^{\circ}\) angle using a compass, we first construct a \(60^{\circ}\) angle and then bisect it to get a \(30^{\circ}\) angle.
Use a compass to bisect angle \(A\hat{B}C = 60^{\circ}\).
Set the width of the compass equal to \(BC\). Place the compass on point \(C\) and draw an arc inside the angle. Without changing the compass width, place the compass on point \(A\) and draw a second arc inside the angle that intersects the first arc (shown as green arcs in the diagram).
Use a ruler to join the vertex (point \(B\)) to the point where the arcs intersect (point \(E\)).
\(BE\) is the bisector of \(A\hat{B}C\).
\(C\hat{B}E = E\hat{B}A = 30^{\circ}\).
We can construct angles of different sizes by constructing a \(60^{\circ}\) angle and then:
Here are a few examples of different types of angles that can be constructed using \(60^{\circ}\):
Construct \(120^{\circ}\) using a compass.
First we construct \(60^{\circ}\) and then subtract the angle from \(180^{\circ}\): \(180^{\circ} − 60^{\circ} = 120^{\circ}\)
Construct \(150^{\circ}\) using a compass.
First we construct \(60^{\circ}\) and then bisect the angle to get \(30^{\circ}\). We can then subtract the angle from \(180^{\circ}\): \(180^{\circ} − 30^{\circ} = 150^{\circ}\)
Construct \(300^{\circ}\) using a compass.
First we construct \(60^{\circ}\) and then subtract the angle from \(360^{\circ}\): \(360^{\circ} − 60^{\circ} = 300^{\circ}\)
Construct \(195^{\circ}\) using a compass.
First we construct \(60^{\circ}\) and then bisect the angle to get \(30^{\circ}\). We bisect the angle again to get \(15^{\circ}\) and then add \(180^{\circ}\): \(180^{\circ} + 15^{\circ} = 195^{\circ}\)
Step 1: Construct \(60^{\circ}\) angle.
Step 2: Bisect \(60^{\circ}\) angle to get \(30^{\circ}\) angle.
Step 3: Subtract \(30^{\circ}\) angle from \(360^{\circ}\) to get \(330^{\circ}\) angle.
Calculation: \(360^{\circ} − \left( \frac{60^{\circ}}{2} \right) = 330^{\circ}\)
Earlier in this chapter, we constructed a perpendicular line at a given point. We know that perpendicular lines intersect at right angles to each other. So we can use this same method for constructing a \(90^{\circ}\) angle.
\(P\) is a point on the line \(AB\). Use a compass to construct \(B\hat{P}Q = 90^{\circ}\).
Place your compass on point \(P\) and draw an arc on each side of point \(P\). Make sure to keep the width of the compass exactly the same when drawing both arcs.
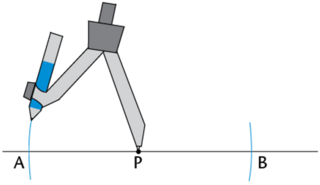
Place the compass on each arc and draw an arc above point \(P\). Label the point of intersection \(Q\).

Use your ruler to join \(P\) and \(Q\).
\(\therefore B\hat{P}Q = A\hat{P}Q = 90^{\circ}\).
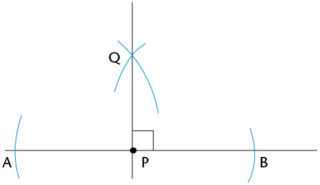
To construct a \(45^{\circ}\) angle using a compass, we first construct a \(90^{\circ}\) angle and then bisect it to get a \(45^{\circ}\) angle.
Use a compass to bisect angle \(B\hat{P}Q = 90^{\circ}\).
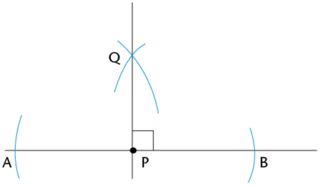
Set the width of the compass equal to \(PB\). Place the compass on point \(B\) and draw an arc inside the angle. Without changing the compass width, place the compass on point \(Q\) and draw a second arc inside the angle that intersects the first arc (shown by the pink arcs in the diagram below). Label point of intersection \(R\).
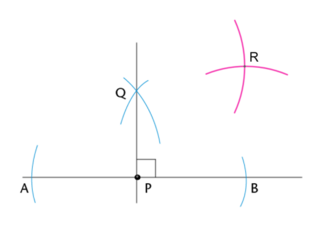
Use a ruler to join the vertex (point \(P\)) to the point where the arcs intersect (point \(R\)).
\(PR\) is the bisector of \(B\hat{P}Q\).
\(\therefore B\hat{P}R = R\hat{P}Q = 45^{\circ}\).
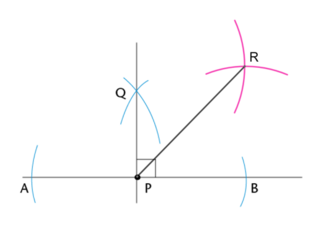
We can construct angles of different sizes by constructing a \(90^{\circ}\) angle and then:
Here are a few examples of different types of angles that can be constructed using \(45^{\circ}\):
Construct \(225^{\circ}\) using a compass.
First we construct \(90^{\circ}\) and then bisect the angle to get \(45^{\circ}\). We can then add \(180^{\circ}\) to the angle:
\[\begin{align} 180^{\circ} + \left( \frac{90^{\circ}}{2} \right) &= 225^{\circ} \\ 180^{\circ} + 45^{\circ} &= 225^{\circ} \end{align}\]Construct \(315^{\circ}\) using a compass.
First we construct \(90^{\circ}\) and then bisect the angle to get \(45^{\circ}\). Then we subtract the angle from \(360^{\circ}\):
\[\begin{align} 360^{\circ} − \left( \frac{90^{\circ}}{2} \right) &= 315^{\circ} \\ 360^{\circ} − 45^{\circ} &= 315^{\circ} \end{align}\]Use a compass to construct \(P\hat{Q}R = 90^{\circ}\).
Aimee wants to construct the following angles using a compass.
Write down each step to show how Aimee would use a \(90^{\circ}\) construction to draw each angle.
Express each answer as a calculation.
Use a compass to construct each angle in Question 2. Use a protractor to check the accuracy of each construction.
Nompumelelo discovered a different method for constructing a \(90^{\circ}\) angle using a compass and a ruler. Her final construction is shown below.
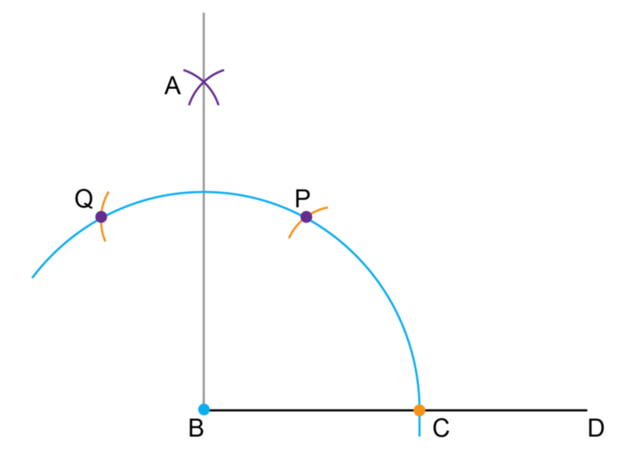
|
Previous
Constructing angles
|
Table of Contents |
Next
Constructing triangles
|