\(\text{2}\); \(\text{4}\); \(\text{8}\); \(\text{16}\);\(\ldots\)
This number sequence starts at \(\text{2}\) and each term is multiplied by \(\text{2}\) to get the next term.
|
Previous
2.4 Inverse proportion patterns, relationships and graphs
|
Next
End of chapter activity
|

Elvis makes boxes of fudge and works out the cost of making the boxes by using a pattern. Look at the table below.
Number of boxes made | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) |
Cost of making the boxes (R) | \(\text{6}\) | \(\text{10}\) | \(\text{14}\) | \(\text{18}\) | \(\text{22}\) | \(\text{26}\) |
In the previous example we described the cost pattern using the number of boxes. This is a very useful thing to do, because it gives us a rule that we can use for any number of boxes!
The rule written in words is: \(\text{cost }= \text{2} + (\text{4} \times \text{ number of boxes})\)
If we use variables to write the rule, we have:
\(c = \text{2} + \text{4}b\), where \(c\) = cost and \(b\) = number of boxes.
Notice that in the pattern in the example above, the cost of making the boxes of fudge depends on the number of boxes made. So the cost (\(c\)) is the dependent variable. The number of boxes (\(b\)) is the independent variable.
Let's call the position of a number in a term \(n\), so that we can use it to describe the value of the term. We call \(n\) a variable, as it can represent different values.
A general formula for any term in the sequence in the table is \((\text{10}n) - \text{5}\).
(Remember that \(\text{10} \times n\) can also be written as \(\text{10}n\).)
So for the 100th term in this sequence, \(n = \text{100}\) and the value of the term is \((\text{10} \times \text{100}) - \text{5} = \text{995}\).
What if you wrote a different number sentence for the pattern? You might have written:
\(\text{5} + [(\)\(\text{1}\)\(- \text{1}) \times \text{10}] = \text{5} + \text{0} = \text{5}\)
\(\text{5} + [(\)\(\text{2}\)\(- \text{1}) \times \text{10}] = \text{5} + \text{10} = \text{15}\)
\(\text{5} + [(\)\(\text{3}\)\(- \text{1}) \times \text{10}] = \text{5} + \text{20} = \text{25}\)
If you replace the number in bold by \(n\), you will get
\(\text{5} + [(n - \text{1}) \times \text{10}]\). You will find that this simplifies as follows:
\(\text{5} + [(n - \text{1}) \times \text{10}]\)
\(= \text{5} + \text{10}n - \text{10}\)
Describe each of these patterns in words, and then write three more terms in each sequence:
\(\text{2}\); \(\text{4}\); \(\text{8}\); \(\text{16}\);\(\ldots\)
This number sequence starts at \(\text{2}\) and each term is multiplied by \(\text{2}\) to get the next term.
\(\text{1}\); \(\text{5}\); \(\text{9}\); \(\text{13}\);\(\ldots\)
This number sequence starts at \(\text{1}\) and \(\text{4}\) is added to each term to get the next term.
\(\text{3}\); \(\text{6}\); \(\text{9}\); \(\text{12}\);\(\ldots\)
This number sequence starts at \(\text{3}\) and \(\text{3}\) is added to each term to get the next term.
\(\text{5}\); \(\text{10}\); \(\text{15}\); \(\text{20}\);\(\ldots\)
This number sequence starts at \(\text{5}\) and \(\text{5}\) is added to each term to get the next term.
Write down the first four terms of the pattern for each of the following descriptions:
This number sequence starts at \(\text{1}\) and \(\text{20}\) is added each time to get the next term.
\(\text{1}\); \(\text{21}\); \(\text{41}\); \(\text{61}\);\(\ldots\)
This number sequence starts at \(\text{1}\) and each term is multiplied by \(\text{4}\) to get the next term.
\(\text{1}\); \(\text{4}\); \(\text{16}\); \(\text{64}\);\(\ldots\)
This number sequence starts at \(\text{20 000}\) and each term is multiplied by \(\text{2}\) to get the next term.
\(\text{20 000}\); \(\text{40 000}\); \(\text{80 000}\); \(\text{160 000}\);\(\ldots\)
Complete the table for the following sequence and use the information to work out the general formula and the value of the 20th term: \(\text{5}\); \(\text{14}\); \(\text{23}\); \(\text{32}\); \(\text{41}\); \(\text{50}\);\(\ldots\)
Position of term (\(n\)) | \(\text{1}\) | \(\text{6}\) | \(\text{20}\) | |||
Value of term | \(\text{5}\) | \(\text{14}\) | \(\text{32}\) | \(\text{41}\) | \(\text{50}\) |
Position of term (n) | \(\text{1}\) | \(\text{2}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) | \(\text{20}\) |
Value of term | \(\text{5}\) | \(\text{14}\) | \(\text{32}\) | \(\text{41}\) | \(\text{50}\) | \(\text{174}\) |
Number sentence: \((n \times \text{9}) - \text{4}\). So 20th term \(=(\text{20} \times \text{9}) - \text{4} = \text{176}\).
Kepa sells pies at a roadside stall. He earns a basic salary of \(\text{R}\,\text{250}\) per day and a commission of \(\text{40}\) \(\text{c}\) on each pie he sells.

Number of pies | \(\text{20}\) | \(\text{40}\) | \(\text{60}\) | \(\text{80}\) | \(\text{100}\) |
Money earned (R) |
Number of pies | \(\text{20}\) | \(\text{40}\) | \(\text{60}\) | \(\text{80}\) | \(\text{100}\) |
Money earned (R) | \(\text{258}\) | \(\text{266}\) | \(\text{274}\) | \(\text{282}\) | \(\text{290}\) |
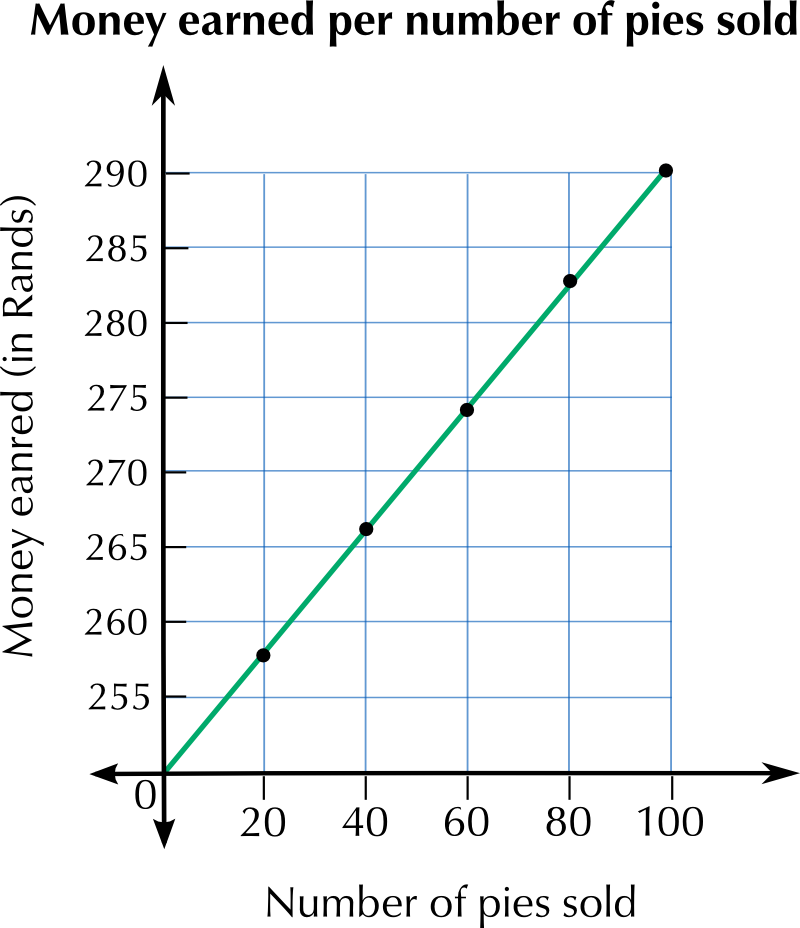
Because the graph is continuous, it will allow him to calculate how much money he earned for any number of pies. The precision with which he can read off the graph however, depends on the intervals between units on the graph's axes.
|
Previous
2.4 Inverse proportion patterns, relationships and graphs
|
Table of Contents |
Next
End of chapter activity
|