Learner-dependent answer.
1.3 Operations using numbers and calculator skills
|
Previous
1.2 Number formats and conventions
|
Next
1.4 Squares, square roots and cubes
|
1.3 Operations using numbers and calculator skills (EMG9)
Estimating (EMGB)
Estimating answers to calculations is a very important step for two reasons:
- it helps you to think about a problem before working it out.
- it helps you to check your answers.
With practice, you can estimate answers quickly!
Estimating answers to calculations is a very important step. Learners can often do calculations without understanding a problem, and estimation guides them to understand the problem thoroughly before using their calculators. It also gives them a way to check their answers thoroughly. Estimating is good practice for mental calculation skills. With practice, learners can estimate quickly.
Using your calculator (EMGC)
Basic calculators usually have these parts:

How to use the memory keys on your calculator
The memory keys (M+, M\(-\), and MRC) allow you to do calculations in the calculator's memory (check what the equivalent keys are on your own calculator).
- The M+ key is used to add a number to the memory, or to add it to a number already in the memory.
- The M\(-\) key is used to subtract a number from the number in memory.
- If you press the MRC key once, the calculator displays the number stored in memory. If you press this key twice, the calculator's memory is cleared.
- When you use a memory key, the letter 'M' appears at the top of the display screen, showing that the number on the display has been stored in the calculator's memory.
This means that we can do longer calculations without having to write down the steps in between. It also gives you a way of doing calculations in the right order. Let's see how this works.
Worked example 4: Using the memory keys on your calculator
Show the correct key sequence on your calculator for working out: \(\text{200} + (\text{2} \times \text{80}) - \text{60}\):
Enter \(\text{200}\) into calculator and add it to the memory by pressing M+.
Calculate \(\text{2} \times \text{80}\) and add it to the memory by pressing M+.
Then enter \(\text{60}\) and subtract it from the memory by pressing M\(-\).
Press MRC to show the answer stored in the memory: \(\text{300}\).
So the complete sequence of keys will be: \(\text{200}\) [M+] \(\text{2}\) [\(\times\)] \(\text{80}\) [M+] \(\text{60}\) [M\(-\)] [MRC]
Compare the key sequence in the previous example to the key sequence: \(\text{200} + \text{2} \times \text{80} - \text{60}\). The memory key allows you to work without brackets.
Changing the sign of numbers
Practise changing the sign of a number on your calculator. For example, changing \(\text{10}\) to \(--\text{10}\). Some calculators have a [\(\pm\)] key, which changes the sign of a number.
If you see \(\pm\) (plus-minus) written before a number in other situations, it means the number is only approximate. It is only on the calculator that this key refers to a function that changes the sign of the number.
Practise using your calculator
This depends on how many digits can be viewed on the screen, but usually it's \(\text{9 999 999 999}\) - or nine billion, nine hundred and ninety-nine million, nine hundred and ninety-nine thousand, nine hundred and ninety-nine
Learner-dependent answer - different calculators have different variations on the “clear” keys. Generally, the “C” key clears everything that is not saved to the calculator's memory and “CE” clears the last step only.
Learner-dependent answer.
\(\text{1 000}\)
\(\text{100}\)
The [C] key has cleared everything, while the [CE] key cleared the last input only.
Learner-dependent answer.
Which of these key sequences do not give you \(--\text{1 000}\) on the display?
Does give \(--\text{1 000}\).
Does give \(--\text{1 000}\).
Does not give \(--\text{1 000}\).
Does give \(--\text{1 000}\).
Does give \(--\text{1 000}\).
Does not give \(--\text{1 000}\).
Does give \(--\text{1 000}\).
Does not give \(--\text{1 000}\).
The order of operations and brackets (EMGD)
Vaneshri makes hand-crafted toys and sells them at three market stalls. She wants to calculate the amount of profit received by her business after the rental costs. Her initial profit is \(\text{R}\,\text{40 000}\). Each stall costs her \(\text{R}\,\text{2 000}\) in rental. She does the following calculation on her calculator:
\(\text{40 000} - \text{2 000} \times \text{3} = \text{114 000}\)
She is very puzzled. How can she have more profit than she started with?
The calculator does the calculations in exactly the same order as they are keyed in:
\begin{align*} &\text{40 000} - \text{2 000} = \text{38 000} \\ &\text{38 000} \times \text{3} = \text{114 000} \end{align*}
This means that she was multiplying the remaining profit by \(\text{3}\), rather than just the rental!
In this context, however, Vaneshri wanted to find the total rental for the \(\text{3}\) stalls (\(\text{2 000} \times \text{3}\)) and then subtract that from \(\text{40 000}\), getting an answer of \(\text{R}\,\text{34 000}\).
There are two ways to make sure that you get the order of operations right. In the following section we will learn about how they work.
Brackets
We can use brackets to show the order in which operations happened in the situation. We want to show that Vaneshri should multiply the stall rental by \(\text{3}\) before subtracting it from the profit:
\(\text{40 000} - (\text{2 000} \times \text{3}) =\text{34 000}\)
BODMAS
If there are no brackets in a calculation, we use the BODMAS rule to remember in which order we must perform operations. This is a rule which says what the order must be:
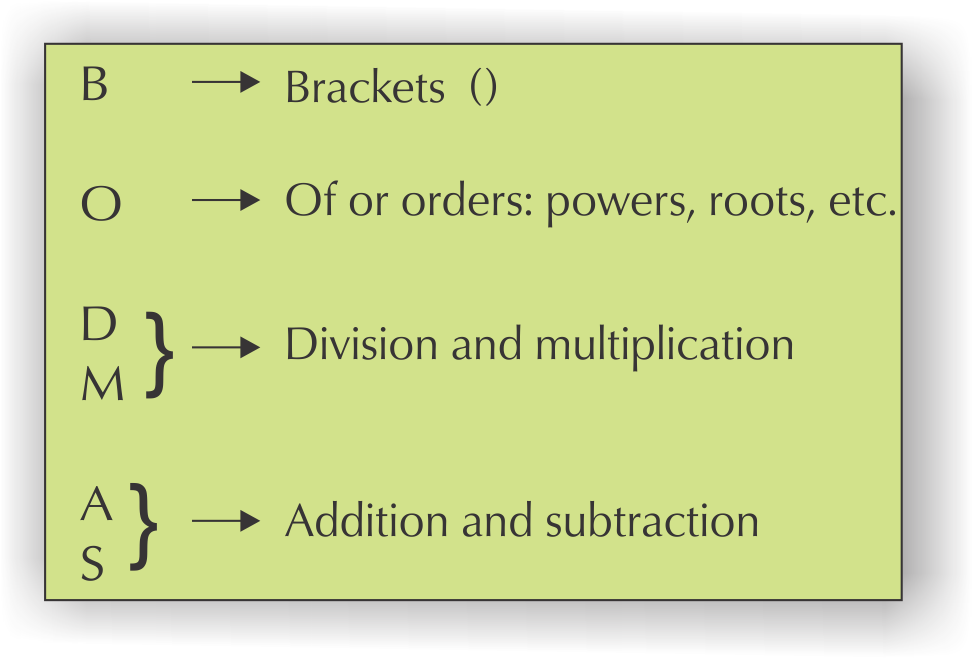
If there are brackets involved then we must do the operation in the brackets first; then do the multiplication or division (it doesn't matter what the order is); and last, do the addition or subtraction (in any order).
Worked example 5: The order of operations
Kepa wrote this number sentence to show the cost of some clothes that he bought:
Cost \(= \text{4} \times \text{R}\,\text{160} + \text{5} \times \text{R}\,\text{85}\)
Work this out using the correct order of operations.
Using BODMAS, we need to calculate the multiplication parts before the addition parts.
\begin{align*} \text{Cost }&= \text{4} \times \text{R}\,\text{160} + \text{5} \times \text{R}\,\text{85} \\ &= \text{R}\,\text{640} + \text{R}\,\text{425} \\ &= \text{R}\,\text{1 065} \end{align*} Using brackets makes this easier to see, but they are not necessary:
\begin{align*} \text{Cost }&= (\text{4} \times \text{R}\,\text{160}) + (\text{5} \times \text{R}\,\text{85}) \\ &= \text{R}\,\text{640} + \text{R}\,\text{42} \\ &= \text{R}\,\text{1 065} \end{align*}
Addition and multiplication shortcuts to make calculations easier (EMGF)
Let's look at some addition and multiplication tricks that help us to calculate quickly and easily, without a calculator. These don't usually apply to subtraction and division.
Remember that we can do addition in any order, for example, \(\text{100} + \text{15} = \text{15} \text{+100}\)
The same applies to multiplication: \(\text{20} \times \text{6} \times \text{8} = \text{8} \times \text{6} \times \text{20}\).
This is useful, because sometimes we can rearrange the order of a calculation to make it easier. We will see how this works below.
Breaking down and multiplying
Breaking down numbers before multiplying is a useful trick for doing mental multiplication quickly. It is a rule that states that you can multiply a large number directly, or break it up into parts and multiply each part, and then add the answers together again. You will get the same answer either way.
For example, if you need to work out \(\text{4} \times \text{57}\) quickly:
\begin{align*} \text{4} \times \text{57}&= \text{4} \times (\text{50} + \text{7}) \text{ (Break up the number \text{57})}\\ &= (\text{4} \times \text{50}) + (\text{4} \times \text{7}) \text{ (Distribute over the parts of \text{57})}\\ &= \text{200} + \text{28}\\ &= \text{228} \end{align*}
It is easy to calculate \((\text{4} \times \text{50}) = \text{200}\) and \((\text{4} \times \text{7}) = \text{28}\) mentally, so you can do the whole calculation without writing it down.
When doing these calculations, look for ways to change the calculation so that you are multiplying by a multiple of ten, or using the multiplication tables that you can do mentally. Sometimes turning a number into a subtraction calculation helps.
Let's see how this rule works in the following examples.
Worked example 6: Breaking down and multiplying
Use breaking down and multiplying to do the following calculations quickly without a calculator.
- How much would it cost to buy \(\text{14}\) CDs at \(\text{R}\,\text{121}\) each?
- How many seats are there in a stadium if there are \(\text{19}\) rows of \(\text{130}\) seats in each row?
-
A school wants to buy \(\text{14}\) computers for the computer lab at \(\text{R}\,\text{10 300}\) each. How much will it cost them in total?

- \begin{align*} \text{121} \times \text{14}&= \text{121} \times (\text{10} + \text{4})\\ &= (\text{121} \times \text{10}) + (\text{121} \times \text{4})\\ &= \text{1 210} + \text{484}\\ &= \text{1 694} \end{align*} OR \begin{align*} (\text{100} + \text{20} + \text{1}) \times \text{14} &= (\text{100} \times \text{14}) + (\text{20} \times \text{14}) + (\text{1} \times \text{14})\\ &= \text{1 400} + \text{280} + \text{14}\\ &= \text{1 694} \end{align*} So it will cost \(\text{R}\,\text{1 694}\).
- \begin{align*} \text{130} \times \text{19}&= \text{130} \times (\text{20} - \text{1}) \text{ (\text{19} is very close to \text{20}, so let's write it as (\text{20} - \text{1}))}\\ &= (\text{130} \times \text{20}) - (\text{130} \times \text{1})\\ &= \text{2 600} - \text{130}\\ &= \text{2 600} - \text{100} - \text{30}\\ &= \text{2 500} - \text{30}\\ &= \text{2 470} \end{align*} (Notice that this last part shows you a way of subtracting more easily by breaking down the number you are subtracting.)
- \begin{align*} \text{10 300} \times \text{14}&= \text{10 300} \times (\text{10} + \text{4})\\ &= (\text{10 300} \times \text{10}) + (\text{10 300} \times \text{4})\\ &= \text{103 000} + \text{41 200}\\ &= \text{144 200} \end{align*} OR \begin{align*} \text{10 300} \times \text{14}&= (\text{10 000} \times \text{14}) + (\text{300} \times \text{14})\\ &= \text{140 000} + \text{4 200}\\ &= \text{144 200} \end{align*} It will cost \(\text{R}\,\text{144 200}\) altogether.
Using grouping
Grouping numbers in different ways can also help us to multiply and add quickly.
There is a rule that states that in a calculation that only contains addition operations, we can group addition calculations in any order, and similarly, in a calculation that only contains multiplication operations, we can group the calculations in any order.
This helps us, because if we rearrange the numbers, we might find that we can do calculations by just looking at them!
In a calculation such as \(\text{25} \times \text{13} \times \text{4}\), it is easier to rewrite this as \(\text{25} \times \text{4} \times \text{13}\) because this becomes \((\text{25} \times \text{4}) \times 13 = \text{100} \times \text{13} = \text{1 300}\).
Worked example 7: Using grouping to make calculations easier
-
There are \(\text{25}\) crates in a shipping container. Each crate contains \(\text{4}\) boxes of \(\text{32}\) ornaments. Using grouping, find an easier way to calculate \(\text{25} \times (\text{32} \times \text{4})\).

- Use grouping to calculate the cost of \(\text{36}\) books at \(\text{R}\,\text{25}\) each (hint: think of \(\text{36}\) as \(\text{9} \times \text{4}\)).
-
A DVD costs \(\text{R}\,\text{250}\). Ibrahim sells \(\text{32}\) of these in one day. How much money does he earn?

- \(\text{25} \times (\text{32} \times \text{4}) = (\text{25} \times \text{4}) \times \text{32}\), which is \(\text{100} \times \text{32} = \text{3 200}\)
- \(\text{R}\,\text{36} \times \text{25} = \text{9} \times \text{4} \times \text{25} = \text{9} \times \text{100} = \text{R}\,\text{900}\)
-
First we break \(\text{32}\) into \(\text{4} \times \text{8}\)
\(\text{R}\,\text{250} \times \text{4} \times \text{8} = \text{R}\,\text{1 000} \times \text{8} = \text{R}\,\text{8 000}\)
Multiplying by \(\text{10}\), \(\text{100}\) and \(\text{1 000}\) without a calculator
Another trick to keep in mind is how we multiply whole numbers by \(\text{10}\), \(\text{100}\) and \(\text{1 000}\).
- To multiply by \(\text{10}\), every digit moves to the left by one decimal place, and a zero moves into the units position.
- To multiply by \(\text{100}\), every digit moves to the left by two decimal places, and two zeros move into the tens and units positions.
- To multiply by \(\text{1 000}\), every digit moves to the left by three decimal places, and three zeros move into the hundreds, tens and units positions.
It is useful to do these calculations in a place value table, or in columns.
Worked example 8: Multiplying by \(\text{10}\), \(\text{100}\) and \(\text{1 000}\)
- Multiply \(\text{39 103}\) by \(\text{10}\).
- Multiply \(\text{5 592}\) by \(\text{100}\).
- Multiply \(\text{123}\) by \(\text{1 000}\).
- Multiply \(\text{7 801}\) by \(\text{1 000}\).
M | H Th | T Th | Th | H | T | U |
\(\text{3}\) | \(\text{9}\) | \(\text{1}\) | \(\text{0}\) | \(\text{3}\) | \(\text{0}\) | |
\(\text{5}\) | \(\text{5}\) | \(\text{9}\) | \(\text{2}\) | \(\text{0}\) | \(\text{0}\) | |
\(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{0}\) | \(\text{0}\) | \(\text{0}\) | |
\(\text{7}\) | \(\text{8}\) | \(\text{0}\) | \(\text{1}\) | \(\text{0}\) | \(\text{0}\) | \(\text{0}\) |
- \(\text{391 030}\)
- \(\text{559 200}\)
- \(\text{123 000}\)
- \(\text{7 801 000}\)
Common fractions (EMGG)
A fraction is a measure of how something is divided into parts.

The fraction \(\frac{\text{5}}{\text{6}}\) means five parts out of a total of six parts, where the whole is divided into \(\text{6}\) parts.

This is called a common fraction. The numerator and the denominator are both whole numbers and they are separated by a line that represents division.
In real life this means five parts out of six, like five people out of a group of six people.
Common fractions are called proper fractions when the numerator is smaller than the denominator, e.g. \(\frac{\text{2}}{\text{10}}\) or \(\frac{\text{3}}{\text{5}}\).
When the numerator is bigger than the denominator, the fraction is called an improper fraction, e.g. \(\frac{\text{10}}{\text{2}}\) or \(\frac{\text{5}}{\text{3}}\).
When we convert improper fractions to whole numbers with a fraction they are called mixed numbers, e.g. \(\frac{\text{9}}{\text{2}} = \text{4}\frac{\text{1}}{\text{2}}\) and \(\frac{\text{4}}{\text{3}} = \text{1} \frac{\text{1}}{\text{3}}\).
Operations with fractions (EMGH)
Adding and subtracting fractions
If you don't use a calculator, you first need to make sure that all fractions have the same denominator before you add or subtract them. Using a calculator often makes calculations with fractions much easier.
Two different methods for adding or subtracting fractions are given below. The method you choose depends on whether you want a common fraction or a decimal fraction as the answer.
Method 1:
To keep your answer as a common fraction, you need to change the denominators of all the fractions you are adding or subtracting to be the same.
- First multiply the denominators together to find a common denominator that will work for all of the fractions. Try to simplify it to make the calculations easier, but remember, it must still be a multiple of all of the original denominators. This demoninator is called the lowest common denominator (LCD).
- Next multiply the numerator of each fraction by the same number you multiplied with the denominator to get the LCD. (e.g. if the original denominator of a fraction is \(\text{3}\), and the LCD of the group of fractions is \(\text{6}\), we multiply the numerator by \(\text{2}\), because \(\text{3}\) \(\times\) \(\text{2}\) = \(\text{6}\)).
For example, how much is \(\frac{\text{1}}{\text{2}} + \frac{\text{1}}{\text{3}} + \frac{\text{1}}{\text{6}}\)?
\(\text{2} \times \text{3} = \text{6}\), so \(\text{6}\) is a common denominator for all three fractions.
Next we multiply each fraction's numerator by the \(\dfrac{\text{LCD}}{\text{denominator}}\).
\begin{align*} &\frac{\text{1}}{\text{2}} + \frac{\text{1}}{\text{3}} + \frac{\text{1}}{\text{6}}\\ & = \frac{(\text{1} \times \frac{\text{6}}{\text{2}}) + (\text{1} \times \frac{\text{6}}{\text{3}}) + (\frac{\text{6}}{\text{6}})}{\text{6}}\\ & = \frac{(\text{1} \times \text{3}) + (\text{1} \times \text{2}) + \text{1}}{\text{6}}\\ &= \frac{\text{6}}{\text{6}}\\ &= \text{1} \end{align*}
Method 2:
Treat each fraction like a separate division calculation, e.g. \(\frac{\text{4}}{\text{5}} = \text{4} \div \text{5}\).
Put the answers of the division calculations into the calculator's memory.
Add to or subtract from the memory and press MRC to find the answer.
Let's put this all together in some worked examples. These look quite complicated, but if you work through them step-by-step, you will see how they work!
Worked example 9: Simplifying fractions
Simplify the following without a calculator and then calculate the decimal answer, using your calculator (round your answer to \(\text{2}\) decimal places):
- \(\frac{\text{3}}{\text{4}} + \frac{\text{3}}{\text{5}} - \frac{\text{3}}{\text{10}}\)
- \(\text{10}\frac{\text{1}}{\text{7}}\)
-
Without a calculator:\begin{align*} &\frac{\text{3}}{\text{4}} + \frac{\text{3}}{\text{5}} - \frac{\text{3}}{\text{10}}\\ &=\frac{(\text{3} \times \text{5})}{\text{20}} + \frac{(\text{3} \times \text{4})}{\text{20}} - \frac{(\text{3} \times \text{2})}{\text{20}} \\ &\text{ (The smallest multiple of \text{4}, \text{5} and \text{10} is \text{20} so \text{20} is the LCD)}\\ &=\frac{\text{15}}{\text{20}} + \frac{\text{12}}{\text{20}} - \frac{\text{6}}{\text{20}} \\ &=\frac{\text{21}}{\text{20}}\\ &=\text{1}\frac{\text{1}}{\text{20}} \end{align*}
With a calculator: Key sequence: \(\text{3}\) [\(\div\)] \(\text{4}\) [=] [M+] \(\text{3}\) [\(\div\)] \(\text{5}\) [=] [M+] \(\text{3}\) [\(\div\)] \(\text{10}\) [=] [M\(-\)] [MRC] =\(\text{1,05}\)
Note: Remember to press [MRC] twice once you have written your answer down.
-
Without a calculator: \(\text{10}\frac{\text{1}}{\text{7}} = \frac{\text{70}}{\text{7}} + \frac{\text{1}}{\text{7}} = \frac{\text{71}}{\text{7}}\) With a calculator: Key sequence: \(\text{10}\) [\(\times\)] \(\text{7}\) [+] \(\text{1}\) [=] [\(\div\)] \(\text{10}\) [=] [M+] =\(\text{10,14285}\)\(\ldots\) Round off \(\text{10,14285}\)\(\ldots\) to the second decimal place = \(\text{10,14}\)
Decimal fractions (EMGJ)
What is a decimal fraction?
Think back to place value: Thousands; Hundreds; Tens and Units.
\(\text{1 000} \div \text{10} = \text{100}\) |
\(\text{100} \div \text{10} = \text{10}\) |
\(\text{10} \div \text{10} = \text{1}\) |
\(\text{1} \div \text{10} = \text{0,1}\) |
The bar below has been divided into ten equal parts; \(\text{1}\) is divided into \(\text{10}\). We say that \(\text{0,1}\) is one tenth. It is the only way in which calculators can write one tenth.

We have found that \(\text{1} \div \text{10} = \text{0,1}\).
Think back to fractions:
\begin{align*} \text{1} \div \text{2} &= \frac{\text{1}}{\text{2}}\\ \text{So } \text{1} \div \text{10} &= \frac{\text{1}}{\text{10}}\\ \text{1} \div \text{10} &= \frac{\text{1}}{\text{10}} = \text{0,1} \end{align*}
\(\text{0,1}\) is just another way of writing \(\frac{\text{1}}{\text{10}}\).
Worked example 10: Working with decimal fractions
What numbers are written in each row of this place value table?
Thousands | Hundreds | Tens | Units | tenths \(\frac{\text{1}}{\text{10}}\) |
\(\text{7}\) | \(\text{1}\) | \(\text{9}\) | \(\text{3}\) | \(\text{6}\) |
\(\text{5}\) | \(\text{0}\) | \(\text{6}\) | \(\text{9}\) | \(\text{1}\) |
- \(\text{7 193}, \text{6} = \text{7} \times \text{1 000} + \text{1} \times \text{100} + \text{9} \times \text{10} + \text{3} \times \text{1} + \frac{\text{6}}{\text{10}}\)
- \(\text{5 069,1} = \text{5} \times \text{1 000} + \text{0} + \text{6} \times \text{10} + \text{9} \times \text{1} + \frac{\text{1}}{\text{10}}\)
Converting between fractions and decimal fractions
To write a common fraction as a decimal fraction, we can use some different methods. First, we can convert the fraction to a fraction with a denominator of \(\text{10}\), \(\text{100}\) or \(\text{1 000}\). For example, \(\frac{\text{1}}{\text{4}} = \frac{\text{25}}{\text{100}} = \text{25}\%\).

How do we write fractions like thirds and sixths as decimal fractions? We can't write them with denominators of \(\text{10}\), \(\text{100}\) or \(\text{1 000}\). Instead, we use division.
Worked example 11: Converting common fractions to decimal fractions
Write these as decimal fractions:
- \(\frac{\text{2}}{\text{3}}\)
- \(\frac{\text{3}}{\text{5}}\)
- We can't write this as a fraction of \(\text{10}\), \(\text{100}\) or \(\text{1 000}\). So we calculate \(\text{2} \div \text{3} = \text{0,6666} \ldots\) This is called a recurring decimal, as it repeats over and over again.
- \(\frac{\text{3}}{\text{5}} = \frac{\text{6}}{\text{10}} = \text{0,6}\)
Converting between fractions and decimal fractions
Using a calculator, write each of these as decimal fractions.
\(\text{0,75}\)
\(\text{0,4}\)
\(\text{0,6}\)
\(\text{0,8}\)
\(\text{1}\)
\(\text{0,25}\)
\(\text{0,333}\)\(\ldots\)
Without a calculator, write down equivalent fractions for each of the following and then write them as decimal fractions:
Fraction | Fraction as tenths | Decimal fraction |
two-thirds | Can't | |
one-quarter | ||
three-quarters | ||
one-fifth | ||
two-fifths | ||
three-fifths | ||
four-fifths | ||
one-sixth | Can't | |
one-eighth |
(Some of the above have more than one decimal place but it is good to know about them.)
Fraction | Fraction as tenths | Decimal fraction |
two-thirds | Can't | \(\text{0,6666666}\) |
one-quarter | Can't | \(\text{0,25}\) |
three-quarters | Can't | \(\text{0,75}\) |
one-fifth | \(\frac{\text{2}}{\text{10}}\) | \(\text{0,2}\) |
two-fifths | \(\frac{\text{4}}{\text{10}}\) | \(\text{0,4}\) |
three-fifths | \(\frac{\text{6}}{\text{10}}\) | \(\text{0,6}\) |
four-fifths | \(\frac{\text{8}}{\text{10}}\) | \(\text{0,8}\) |
one-sixth | Can't | \(\text{0,166666666}\) |
one-eighth | Can't | \(\text{0,128}\) |
Positive and negative numbers (EMGK)
Negative numbers are numbers that are smaller than zero. Although they are obvious to us, people only started using negative numbers in the late middle ages. If we didn't include negative numbers, there would be many subtraction calculations that we couldn't do.
A number line helps us to understand negative numbers. We can place \(\text{0}\) on a number line and then numbers \(\text{1}\) to \(\text{5}\) to the right of the \(\text{0}\). 
Now think about a point that is one unit space to the left of the \(\text{0}\) point. We cannot call this point \(\text{1}\), as there is already a point called \(\text{1}\). We therefore call this point \(--\text{1}\) (or minus one), as it is one unit to the left of \(\text{0}\).
Notice that the plus and minus signs now have two meanings:
- The plus sign can indicate addition or a positive number.
- The minus sign can indicate subtraction or a negative number.
To avoid any confusion between “sign” and “operation,” rather read the sign of a number as “positive” or “negative.” When “\(+\)” is used as an operation sign, read it as “plus.” When “\(-\)” is used as an operation sign, read it as “minus.”
Positive and negative numbers as opposites
Every positive number has an opposite negative number on the other side of zero. If you add these two numbers together, the answer is zero.
For example, \(\text{4} + (--\text{4}) = \text{0}\). This is the same as subtracting \(\text{4}\) from \(\text{4}\).
Fractions, decimal fractions and positive and negative numbers
Share \(\text{11}\) sausage rolls equally among \(\text{10}\) learners. How much sausage roll will each learner receive?

\(\text{1}\frac{\text{1}}{\text{10}}\)
\(\text{1}\frac{\text{1}}{\text{5}}\)
\(\text{1}\frac{\text{1}}{\text{2}} = \frac{\text{6}}{\text{4}} = \frac{\text{3}}{\text{4}} + \frac{\text{6}}{\text{4}} = \frac{\text{9}}{\text{4}}\).
Write the following numbers in a place value table:
- \(\text{64,8}\)
- \(\text{341,2}\)
- \(\text{6 909,9}\)
Thousands | Hundreds | Tens | Units | tenths \(\frac{\text{1}}{\text{10}}\) |
\(\text{6}\) | \(\text{4}\) | \(\text{8}\) | ||
\(\text{3}\) | \(\text{4}\) | \(\text{1}\) | \(\text{2}\) | |
\(\text{6}\) | \(\text{9}\) | \(\text{0}\) | \(\text{9}\) | \(\text{9}\) |
Write as decimals:
\(\text{3,8}\)
\(\text{1,3}\)
\(\text{5,25}\)
\(\text{4,5}\)
From ; = write down the correct sign to make the following true:
\(
\(
\(
\(>\)
Write down the number that is:
\(\text{46,0}\)
\(\text{9,99}\)
\(\text{R}\,\text{4 000}\) \(-\) (\(-\) \(\text{R}\,\text{2 000}\)) = \(\text{R}\,\text{6 000}\)
|
Previous
1.2 Number formats and conventions
|
Table of Contents |
Next
1.4 Squares, square roots and cubes
|
