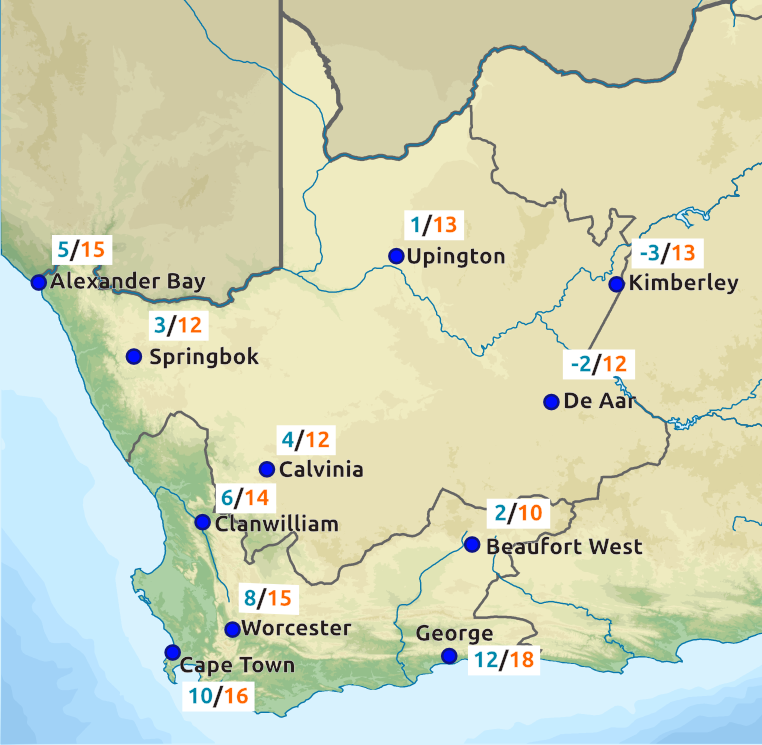
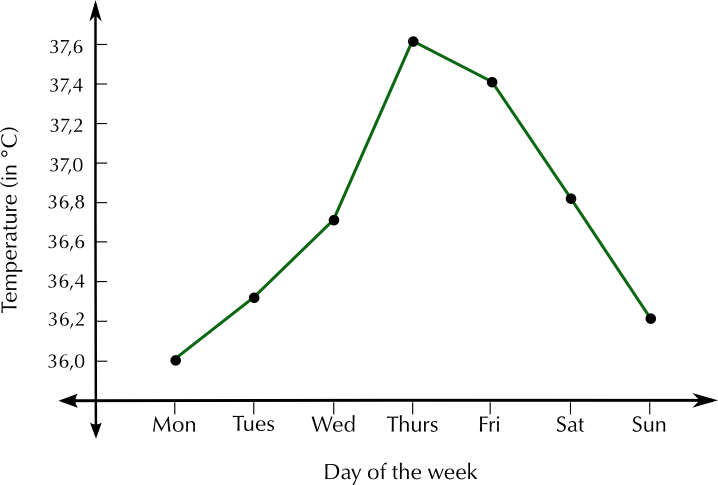
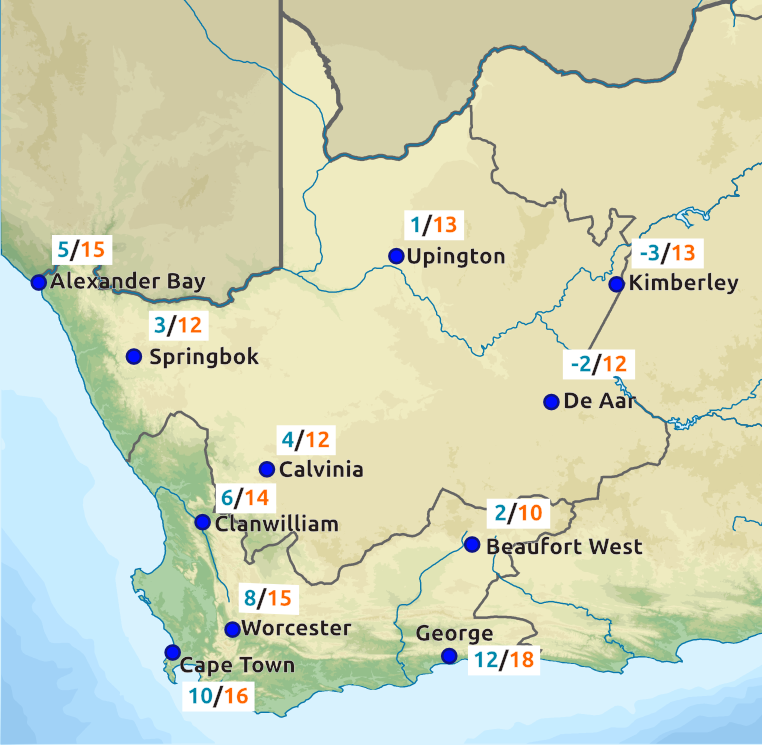
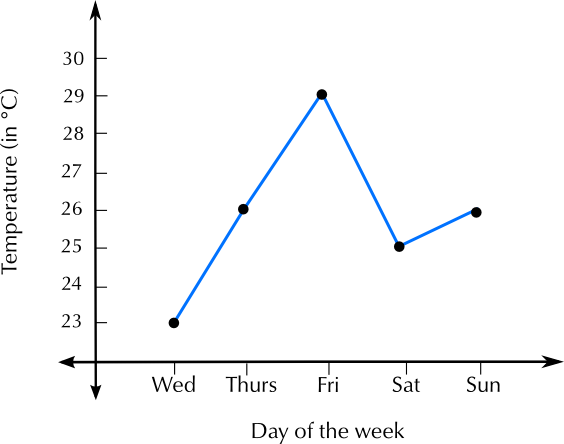
Katie is going to bake fish and potatoes for dinner. On the box of frozen fish, the instructions say “Cook for \(\text{20}\) min at \(\text{200}\)\(\text{°C}\)”. Her recipe for baked potatoes needs the oven temperature to be \(\text{120}\)\(\text{°C}\). What is the temperature difference between these two temperatures?

\(\text{200}\)\(\text{°C}\) - \(\text{120}\)\(\text{°C}\) = \(\text{80}\)\(\text{°C}\)
Bheki lives in Durban. He knows that at sea level, water boils at \(\text{100}\)\(\text{°C}\). He is trying to boil water in a kettle on the stove. If the water is \(\text{72}\)\(\text{°C}\), how much hotter does it need to be (in °C) before it will start boiling?
\(\text{100}\)\(\text{°C}\) \(-\) \(\text{72}\)\(\text{°C}\) = \(\text{28}\)\(\text{°C}\) hotter
Marie wants to make ice cubes. She knows that water freezes at \(\text{0}\)\(\text{°C}\). She measures the temperature of the water in the ice tray to be \(\text{23}\)\(\text{°C}\). How much colder (in °C) does the water have to be before it will freeze?
\(\text{23}\)\(\text{°C}\) \(-\) \(\text{0}\)\(\text{°C}\) = \(\text{23}\)\(\text{°C}\) colder.