\(\text{R}\,\text{400}\), the sixth withdrawal
\(\text{R}\,\text{3,30}\) + \(\text{4}\) \(\times\) \(\text{R}\,\text{1,20}\) = \(\text{R}\,\text{8,10}\)
|
Previous
11.4 Value Added Tax
|
Next
12.1 Introduction and key concepts
|
The TownBank current account charges \(\text{R}\,\text{3,30}\) plus \(\text{R}\,\text{1,20}\) per \(\text{R}\,\text{100}\) or part thereof for a cash withdrawal from a TownBank ATM. The first five withdrawals in a month are free. Determine the bank charges for a withdrawal of:
\(\text{R}\,\text{400}\), the sixth withdrawal
\(\text{R}\,\text{3,30}\) + \(\text{4}\) \(\times\) \(\text{R}\,\text{1,20}\) = \(\text{R}\,\text{8,10}\)
\(\text{R}\,\text{850}\), the fourth withdrawal
Free
\(\text{R}\,\text{3 000}\), the tenth withdrawal
\(\text{R}\,\text{3,30}\) + \(\text{30}\) \(\times\) \(\text{R}\,\text{1,20}\) = \(\text{R}\,\text{15,30}\)
\(\text{R}\,\text{250}\), the seventh withdrawal
\(\text{R}\,\text{3,30}\) + \(\text{3}\) \(\times\) \(\text{R}\,\text{1,20}\) = \(\text{R}\,\text{6,90}\)
The Success Current Account charges \(\text{R}\,\text{3,75}\) plus \(\text{R}\,\text{0,75}\) per full \(\text{R}\,\text{100}\), to a maximum charge of \(\text{R}\,\text{25,00}\) for debit card purchases. Determine the charges for a purchase of:
\(\text{R}\,\text{374,55}\)
\(\text{R}\,\text{3,75}\) + \(\text{3}\) \(\times\) \(\text{R}\,\text{0,75}\) = \(\text{R}\,\text{6,00}\)
\(\text{R}\,\text{990,87}\)
\(\text{R}\,\text{3,75}\) + \(\text{9}\) \(\times\) \(\text{R}\,\text{0,75}\) = \(\text{R}\,\text{10,50}\)
\(\text{R}\,\text{2 900,95}\)
\(\text{3,75}\) + \(\text{29}\) \(\times\) \(\text{R}\,\text{0,75}\) = \(\text{R}\,\text{25,50}\). This exceeds the maximum charge or \(\text{R}\,\text{25}\), so the bank charge will be \(\text{R}\,\text{25,00}\).
You are given the following information about bank charges for a TownBank current account.

Withdrawals
Over the counter: \(\text{R}\,\text{23,00}\) plus \(\text{R}\,\text{1,10}\) per \(\text{R}\,\text{100}\) or part thereof
TownBank ATM: \(\text{R}\,\text{3,50}\) plus \(\text{R}\,\text{1,10}\) per \(\text{R}\,\text{100}\) or part thereof
Another bank's ATM: \(\text{R}\,\text{5,50}\) plus \(\text{R}\,\text{3,50}\) plus \(\text{R}\,\text{1,10}\) per \(\text{R}\,\text{100}\) or part thereof
Tillpoint - cash only: \(\text{R}\,\text{3,65}\)
Tillpoint - cash with purchase: \(\text{R}\,\text{5,50}\)
Calculate the fee charged for a \(\text{R}\,\text{2 500}\) withdrawal from a TownBank ATM.
\(\text{R}\,\text{3,50}\) + \(\text{25}\) \(\times\) \(\text{R}\,\text{1,10}\) = \(\text{R}\,\text{31,00}\)
Calculate the fee charged for a \(\text{R}\,\text{750}\) withdrawal from another bank's ATM.
\(\text{R}\,\text{5,50}\) + \(\text{R}\,\text{3,50}\) + \(\text{8}\) \(\times\) \(\text{R}\,\text{1,10}\) = \(\text{R}\,\text{17,80}\)
Calculate the fee charged for a \(\text{R}\,\text{250}\) withdrawal from the teller at a branch.
\(\text{R}\,\text{23,00}\) + \(\text{3}\) \(\times\) \(\text{R}\,\text{1,10}\) = \(\text{R}\,\text{26,30}\)
What percentage of the \(\text{R}\,\text{250}\) withdrawal in question (c) is charged in fees?
\(\frac{\text{26,30}}{\text{250}} \times \text{100}\)=\(\text{10,52}\%\)
Would it be cheaper to withdraw \(\text{R}\,\text{1 500}\) at the bank, from a TownBank ATM or from a till point with a purchase?
At the bank: \(\text{R}\,\text{23}\) + \(\text{15}\) \(\times\) \(\text{R}\,\text{1,10}\) = \(\text{R}\,\text{39,50}\). At a TownBank ATM: \(\text{R}\,\text{3,50}\) + \(\text{15}\) \(\times\) \(\text{R}\,\text{1,10}\) = \(\text{R}\,\text{20,00}\). At a tillpoint with a purchase: \(\text{R}\,\text{5,50}\). So it will be cheapest to draw at a tillpoint, with a purchase.
Study the graph and answer the questions that follow:
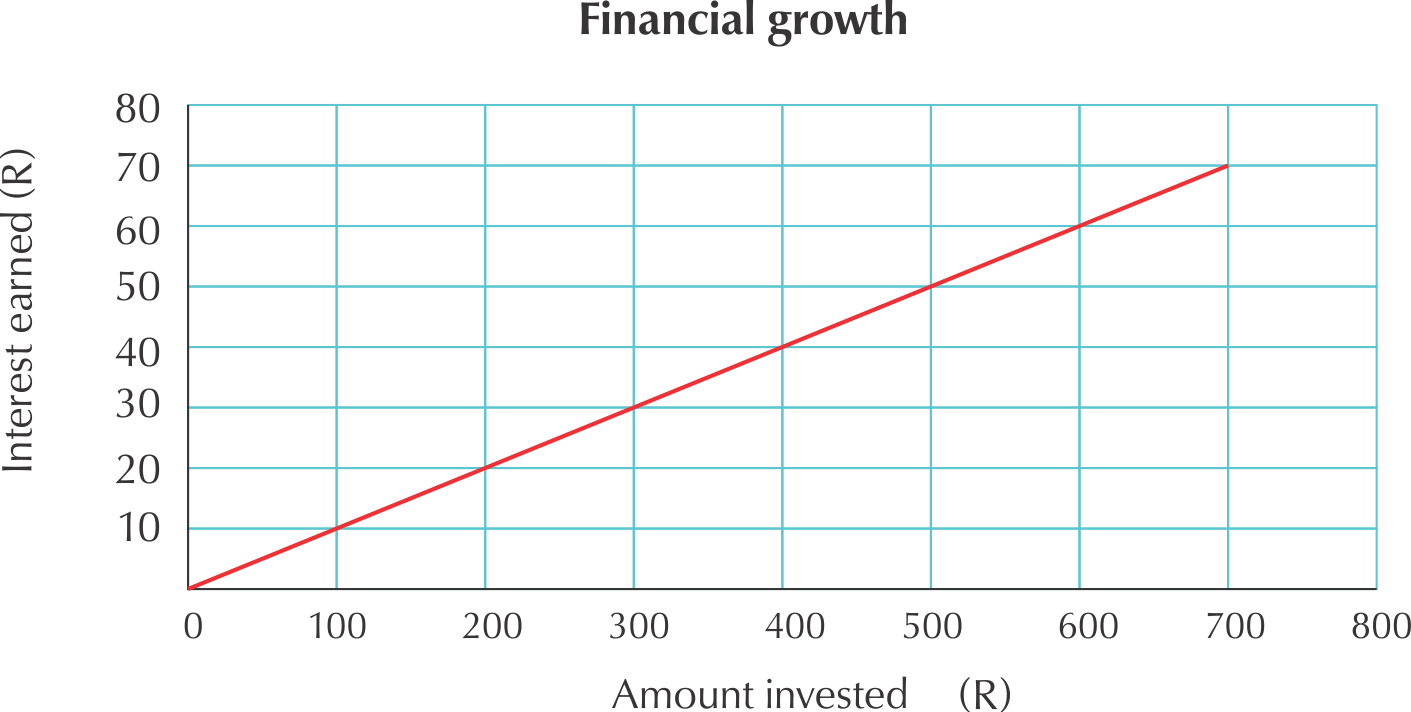
Complete the table below: (Fill in all the missing spaces)
Amount invested (in Rands) | \(\text{100}\) | \(\text{200}\) | \(\text{300}\) | \(\text{400}\) | \(\text{500}\) | \(\text{600}\) | \(\text{700}\) |
Interest Earned (in Rands) | \(\text{10}\) | \(\text{30}\) | \(\text{50}\) | \(\text{70}\) | |||
Interest/Amount \(\times\) \(\text{100}\) (Interest Rate) |
Amount invested in Rands | \(\text{100}\) | \(\text{200}\) | \(\text{300}\) | \(\text{400}\) | \(\text{500}\) | \(\text{600}\) | \(\text{700}\) |
Interest Earned in Rands | \(\text{10}\) | \(\text{20}\) | \(\text{30}\) | \(\text{40}\) | \(\text{50}\) | \(\text{60}\) | \(\text{70}\) |
Interest/Amount \(\times\) \(\text{100}\) (Interest Rate) | \(\text{10}\%\) | \(\text{10}\%\) | \(\text{10}\%\) | \(\text{10}\%\) | \(\text{10}\%\) | \(\text{10}\%\) | \(\text{10}\%\) |
What kind of proportionality exists between the amount invested and the interest earned?
Direct proportionality.
You decide to invest \(\text{R}\,\text{10 000}\). Calculate the amount of interest you can expect to earn.
Interest rate is fixed at \(\text{10}\%\). \(\text{10}\%\) of \(\text{R}\,\text{10 000}\) = \(\text{R}\,\text{1 000}\) of interest earned.
Complete the table below by calculating the missing amounts.
Amount (R) | \(\text{17,95}\) | \(\text{33,80}\) | \(\text{4,50}\) | ||||
VAT (R) | \(\text{2,51}\) | \(\text{14,00}\) | \(\text{1,4}\) | ||||
Total (R) | \(\text{20,46}\) | \(\text{11,40}\) | \(\text{221}\) | \(\text{404,00}\) |

Amount (R) | \(\text{17,95}\) | \(\text{100,00}\) | \(\text{10,00}\) | \(\text{33,80}\) | \(\text{4,50}\) | \(\text{193,86}\) | \(\text{354,39}\) |
VAT (R) | \(\text{2,51}\) | \(\text{14,00}\) | \(\text{1,4}\) | \(\text{4,73}\) | \(\text{0,63}\) | \(\text{27,14}\) | \(\text{49,61}\) |
Total (R) | \(\text{20,46}\) | \(\text{114,00}\) | \(\text{11,40}\) | \(\text{38,53}\) | \(\text{5,13}\) | \(\text{221,00}\) | \(\text{404,00}\) |
|
Previous
11.4 Value Added Tax
|
Table of Contents |
Next
12.1 Introduction and key concepts
|