Revision

Show all your steps in your working.

Algebraic expressions

  1. Simplify:
    1. \(x^2 + x^2\)
    2. \(m + m \times m + m\)
    3. \(5ab - 7a^2 - 2a^2 + 11ba\)
    4. \((3ac^2)(-4a^2b)\)
    5. \((-4a^{2}b^{3})^3\)
    6. \((\frac{-6x^2yz^4}{3xyz})^2\)
    7. \(\sqrt{\frac{100x^4}{81y^{64}}}\)
    8. \(\sqrt{16c^2 + 9c^2}\)
    9. \((2x + 3x)^3\)
    10. \(3x^2(4x^3 - 5)\)
    11. \((4a - 7a)(a^2 - 2a - 5)\)
    12. \(\frac{9c^2de^3}{3c^2d^2e^2f}\)
    13. \(\frac{6b^2 - 3b^2}{2b^2}\)
    14. \(\frac{10x^2 - 5x + 1}{5}\)
    15. \(\frac{14x -21x^2}{7x^2}\)
  2. Simplify the following expressions:
    1. \( 3(a+ 2b) - 4(b - 2a)\)
    2. \( 3 - 2(5x^2 + 6x - 2)\)
    3. \( 2x(x^2 - x + 1) - 3(4 - x)\)
    4. \( (2a + b - 4c) - (5a + b - c)\)
    5. \(a\{2a^2[4 + 2(3a + 1)] - a\}\)
  3. If \(a = 0, ~b = -2\), and \(c = 3\), determine the value of the following without using a calculator. Show all working:
    1. \(b^2c \)
    2. \(2b - b(ab - 5bc) \)
    3. \(\frac{2b + c - 10a}{3c^2}\)
  4. If \(y = -2\), find the value of \(2y^3 - 4y + 3\)

Algebraic equations

  1. Solve the following equations:
    1. \( -x = -7\)
    2. \( 2x = 24\)
    3. \( 3x - 6 = 0\)
    4. \( 2x + 5 = 3\)
    5. \( 3(x - 4) = -3\)
    6. \( 4(2x - 1) = 5(x - 2)\)
  2. Sello is \(x\) years old. Thlapo is 4 years older than Sello. The sum of their ages is 32.
    1. Write this information in an equation using \(x\) as the variable.
    2. Solve the equation to find Thlapo's age.
  3. The length of a rectangle is \(2x + 8\) cm and the width is 2 cm. The area of the rectangle is 12 cm\(^2\).
    1. Write this information in an equation using \(x\) as the variable.
    2. Solve the equation to determine the value of \(x\).
    3. How long is the rectangle?
  4. The area of a rectangle is \((8x^2 + 2x)\) cm\(^2\), and the length is \(2x\) cm. Determine the width of the rectangle in terms of \(x\), in its simplest form.

Construction of geometric figures

Do not erase any construction arcs in these questions.

    1. Construct \(\hat{DEF} = 56^{\circ}\) with your ruler, pencil, and a protractor. Label the angle correctly.
    2. Bisect \(\hat{DEF}\) using only a compass, ruler, and pencil (no protractor).
  2. Here is a rough sketch of a quadrilateral (NOT drawn to scale):

    85304.png

    Construct the quadrilateral accurately.

  3. Using only a compass, ruler and pencil, construct:
    1. A line through C perpendicular to AB
    2. A line through D perpendicular to AB

    85685.png

  4. Construct and label the following triangles and quadrilaterals:
    1. Triangle ABC, where AB = 8 cm; BC = 5,5 cm and AC = 4,9 cm
    2. Rhombus GHJK, where GH = 6 cm and \( \hat{G} = 50^{\circ}\)
  5. Here is a rough sketch of triangle FGH (NOT drawn to scale):

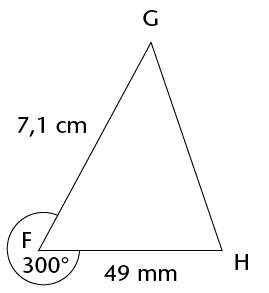
    85250.png

    Using a ruler, pencil, and protractor, construct and label the triangle accurately.

  6. Construct an angle of 120° without using a protractor.

Geometry of shapes

  1. True or false: all equilateral triangles, no matter what size they are, have angles that equal 60°.
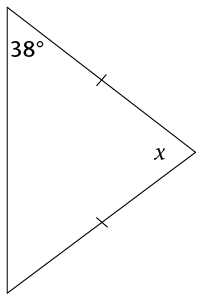
    1. In a triangle, two of the angles are 35° and 63°. Calculate the size of the third angle.
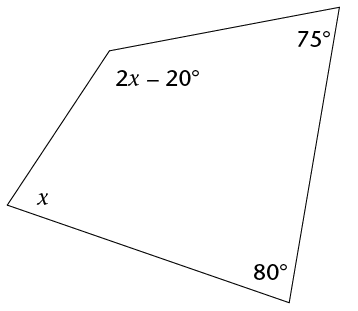
    2. In a quadrilateral, one of the angles is a right angle, and another is 80°. If the remaining two angles are equal to each other, what is the size of each?
  3. If triangle MNP has \(\hat{M} = 40^{\circ}\) and \(\hat{N} = 90^{\circ}\), what is the size of \(\hat{P}\)?
  4. Write definitions of the triangles in the table below.

    Equilateral triangle

    Isosceles triangle

    Right-angled triangle
  5. The following list gives the properties of three quadrilaterals, A, B and C.
    1. Give the special names of each of shapes A, B and C.

      Quadrilateral A: The opposite sides are equal and parallel.

      Quadrilateral B: The adjacent sides are equal, while the opposite sides are not equal.

      Quadrilateral C: All of the angles are right angles.

    2. What property must Quadrilateral A also have to make it a rhombus?
    3. What property must Quadrilateral A also have to make it a rectangle?
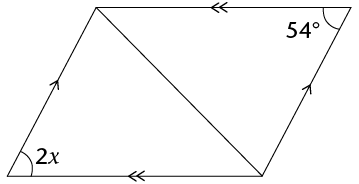
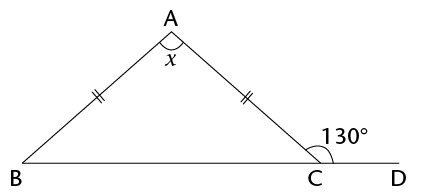
  6. Determine the size of \(\hat{V}\). Show all steps of your working and give reasons.
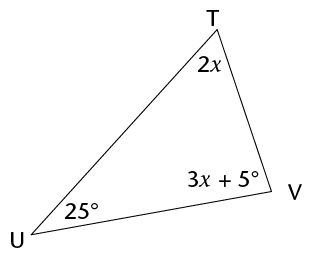
    85169.png
  7. Determine the size of \(x\). Give reasons.
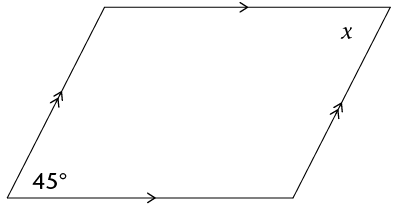
    85145.png

Geometry of straight lines

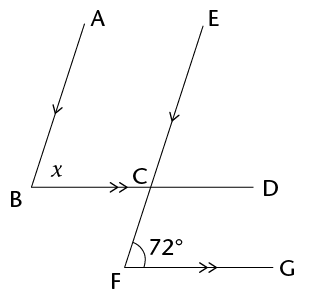
  1. Study the diagram alongside:
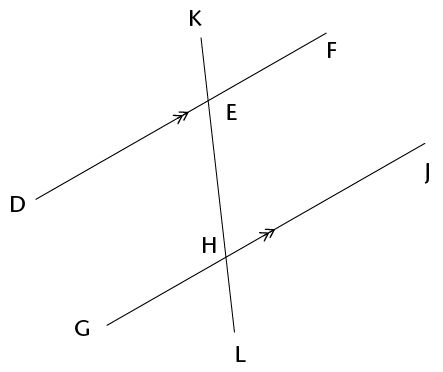
    85137.png
    1. Name an angle that is vertically opposite to \(\hat{EHG}\).
    2. Name an angle that is corresponding to \(\hat{EHG}\).
    3. Name an angle that is co-interior with \(\hat{EHG}\).
    4. Name an angle that is alternate to\(\hat{EHG}\).
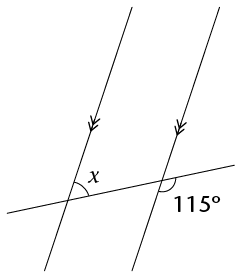
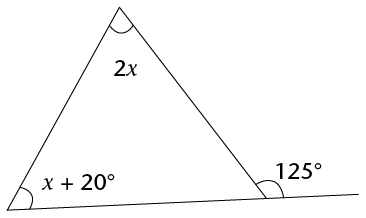
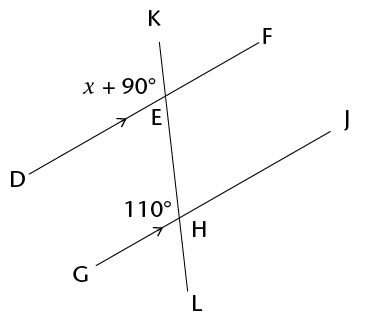
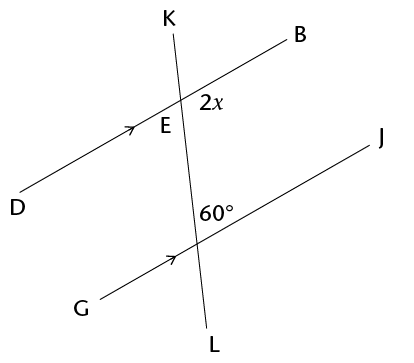
  2. Determine the size of \(x\) in each of the following diagrams. Show all steps of working and give reasons.
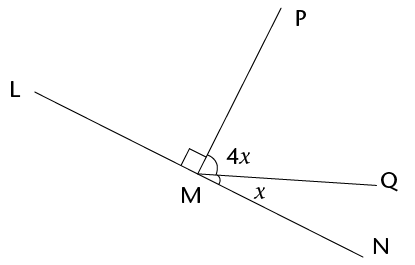
    1. 85080.png
    2. 85063.png
    3. 85049.png
    4. 85041.png
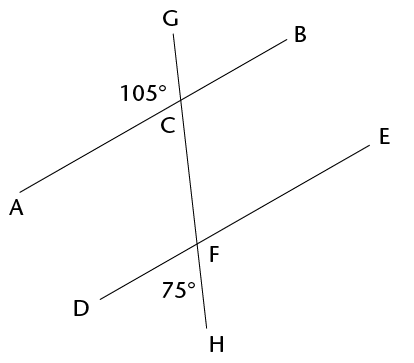
    5. Are line segments AB and DE parallel? Prove your answer.
      85016.png

Assessment

In this section, the numbers in brackets at the end of a question indicate the number of marks the question is worth. Use this information to help you determine how much working is needed. The total number of marks allocated to the assessment is 75.

  1. Simplify the following expressions:
    1. \(5x^2 - 6x^2 + 10x^2\)
    2. \(4(3x - 7) - 3(2 + x)\)
    3. \((-2a^2bc^3)2 \div 4abcd\)
    4. \(\frac{2x(3x-15)}{3x}\)
    5. \(\sqrt[3]{108d^15 \div 4d^6}\)
    6. \(2[3x^2 - (4 - x^2)] - [9 + (4x)^2]\)
  2. Find the value of \(a\) if \(b = 3,~ c = -4\) and \(d = 2\):
    1. \(a = b + c \times d\)
    2. \(ab^2 = 2c - d \div 2\)
  3. Solve the following equations:
    1. \( -7x = 56\)
    2. \(4(x + 3) = 16\)
  4. Sipho, Fundiswa and Ntosh are brothers. Sipho earns Rx per month; Fundiswa earns R1 000 more than Sipho per month, and Ntosh earns double what Sipho earns. If you add their salaries together you get a total of R27 000.
    1. Write this information in an equation using \(x\). (2)
    2. Solve the equation to find how much Fundiswa earns per month. (2)
  5. Construct the following figure using only a pencil, ruler and compass. Do not erase any construction arcs.
    1. An angle of 60° (2)
    2. The perpendicular bisector of line VW, where VW = 10 cm
    3. Triangle KLM, where KL = 8,3 cm; LM = 5,9 cm and KM = 7 cm
    4. Parallelogram EFGH, where E = 60°, EF = 4,2 cm and EH = 8 cm
    1. What is/are the property/properties that make a rhombus different to a parallelogram? (1)
    2. True or false: a rectangle is a special type of parallelogram. (1)
  7. Determine the size of x in each figure. Show all the necessary steps and give reasons.
    1. 84881.png
    2. 84869.png
    3. 84859.png
  8. Study the following diagram. Then answer the questions that follow:

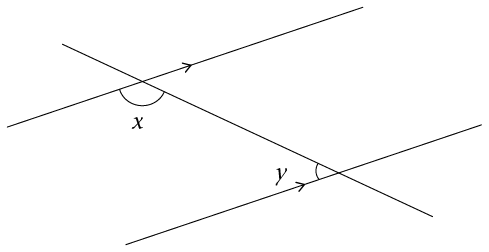
    84849.png

    1. Write down the correct word to complete the sentence: \(x\) and \(y\) form a pair of __________________ angles (1)
    2. Write down an equation that shows the relationship between angles \(x\) and \(y\). (1)
  9. Determine the size of \(x\), showing all necessary steps and giving reasons for all statements that use geometrical theorems:
    1. 84815.png
    2. 84805.png
    3. 84797.png
  10. Consider the following diagram, in which it is given: \(\hat{DEI} = 30^{\circ}, ~DE = EI, ~DF \parallel IG\), and \(GH = IH\).

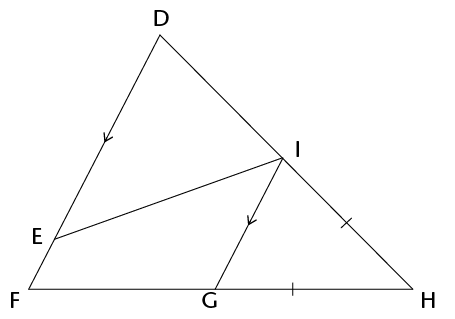
    84769.png

    1. Determine, with reasons, the size of \(\hat{H}\). (6)
    2. Which of the following statements is correct? Explain your answer. (2)
      1. \( \triangle DEI\) is similar to \( \triangle GHI\)
      2. \( \triangle DEI\) is congruent to \( \triangle GHI\)
      3. We cannot determine a relationship between \( \triangle DEI\) and \( \triangle GHI\) since there is not enough information given.

        Statement ______ is correct because