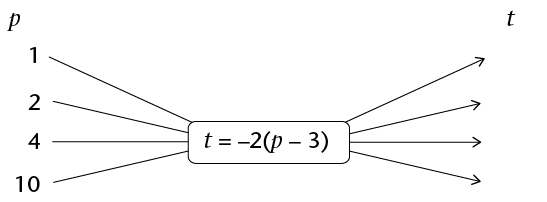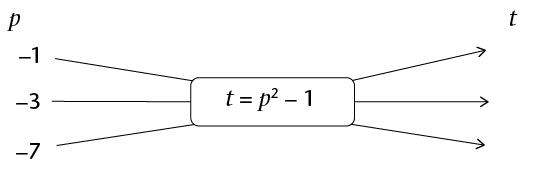Chapter 9: Chapter algebraic expressions

Chapter 8: Term revision and assessment

Revision

Show all your steps of working.

Whole numbers

1. Write both 300 and 160 as products of prime factors.
2. Determine the HCF and LCM of 300 and 160.
Tommy, Thami and Timmy are given birthday money by their grandmother in the ratio of their ages. They are turning 11, 13 and 16 years old, respectively. If the total amount of money given to all three boys is R1 000, how much money does Thami get on his birthday?
Tshepo and his family are driving to the coast on holiday. The distance is 1 200 km and they must reach their destination in 12 hours. After 5 hours, they have travelled 575 km. Then one of their tyres bursts. It takes 45 minutes to get the spare wheel on, before they can drive again. At what average speed must they drive the remainder of the journey to reach their destination on time?
The number of teachers at a school has increased in the ratio 5 : 6. If there used to be 25 teachers at the school, how many teachers are there now?
ABC for Life needs to have their annual statements audited. They are quoted R8 500 + 14% VAT by Audits Inc. How much will ABC for Life have to pay Audits Inc. in total?
Reshmi invests R35 000 for three years at an interest rate of 8,2% per annum. Determine how much money will be in her account at the end of the investment period.
Lesebo wants to buy a lounge suite that costs R7 999 cash. He does not have enough money and so decides to buy it on hire purchase. The store requires a 15% deposit up front, and 18 monthly instalments of R445.
1. Calculate the deposit that Lesebo must pay.
2. How much extra does Lesebo pay because he buys the lounge suite on hire purchase, rather than in cash?

Consider the following exchange rates table:

South African Rand	1.00 ZAR	inv. 1.00 ZAR
Euro	0.075370	13.267807
US Dollar	0.098243	10.178807
British Pound	0.064602	15.479409
Indian Rupee	5.558584	0.179902
Australian Dollar	0.102281	9.776984
Canadian Dollar	0.101583	9.844200
Emirati Dirham	0.360838	2.771327
Swiss Franc	0.093651	10.677960
Chinese Yuan Renminbi	0.603065	1.658195
Malaysian Ringgit	0.303523	3.294646

Write down the amount in rand that needs to be exchanged to get 1 Swiss franc. Give your answer to the nearest cent.
Write down the only currency for which an exchange of R100 will give you more than 100 units of that currency.
Ntsako is travelling to Dubai and converts R10 000 into Emirati dirhams. How many dirhams does Ntsako receive (assume no commission)?

Integers

Don't use a calculator for any of the questions in this section.

Write a number in each box to make the calculations correct.
1. ☐ + ☐ = -11
2. ☐ - ☐ = -11
Fill <, > or = into each block to show the relationships.
1. -23 ☐ 20
2. -345 ☐ -350
3. \(4 - 3\) ☐ \(3 - 4\)
4. \(5 - 7\) ☐ \(-(7 - 5)\)
5. \(-9 \times 2\) ☐ \(-9 \times -2\)
6. \( -4 \times 5\) ☐ \(4 \times -5\)
7. \( -10 \div 5 ☐ -10 \div -2 \)
8. \(-15 \times -15\) ☐ 224
Follow the pattern to complete the number sequences.
1. 8; 5; 2;☐
2. 2; -4; 8;☐
3. -289; -293; -297;☐
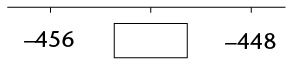
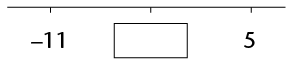
Look at the number lines. In each case, the missing number is halfway between the other two numbers. Fill in the correct values in the boxes.
Calculate the following:
1. \( -5 - 7\)
2. \( 7 - 10\)
3. \( 8-(-9)\)
4. \( (-5)(-2)(-4)\)
5. \( 5 + 4 \times 2\)
6. \( \frac{(\sqrt{4})(-2)^2}{-4}\)
7. \( \frac{-(-3)^3\sqrt[3]{125}}{(-9)(3)}\)
8. \( \frac{\sqrt[3]{-64}}{-3-1}\)
1. Write down two numbers that multiply to give -15. (One of the numbers must be positive and the other negative.)
2. Write down two numbers that add to 15. One of the numbers must be positive and the other negative.
At 5 a.m., the temperature in Kimberley was -3 °C. At 1 p.m., it was 17 °C. By how many degrees had the temperature risen?
A submarine is 220 m below the surface of the sea. It travels 75 m upwards. How far below the surface is it now?

Exponents

You should not use a calculator for any of the questions in this section.

Write down the value of the following:
1. \((-3)^3\)
2. \(-5^2\)
3. \( (-1)^{200}\)
4. \( (10^2)^2\)
Write the following numbers in scientific notation:
1. 200 000
2. 12,345
Write the following numbers in ordinary notation:
1. \(1,3 \times 10^2 \)
2. \(7,01 \times 10^7 \)
Which of the following numbers is bigger: \(5,23 \times 10^{10}\) or \(2 ,9 \times 10^{11}\)?
Simplify the following:
1. \(2^7 \times 2^3\)
2. \(2x^3 \times 4x^4\)
3. \((-8y^6) \div (4y^3)\)
4. \((3x^8)^3\)
5. \( (2x^5)(0.5x^{-5})\)
6. \( (-3a^2b^3c)(-4abc^2)^2\)
7. \( \frac{(2xy^2z^3)(-5y^2z)^2}{20xy^8z^4} \)
Write down the values of each of the following:
1. \((0,6)^2\)
2. \((0,2)^3\)
3. \((\frac{1}{2})^5\)
4. \(\sqrt{\frac{1}{4}}\)
5. \(4\sqrt{\frac{9}{64}}\)
6. \(\sqrt[3]{0.001}\)

Numeric and geometric patterns

For each of the following sequences, write the rule for the relationship between each term and the following term in words. Then use the rule to write the next three terms in the sequence.
1. \(12; 7; 2;\text{______};\text{______};\text{______}\)
2. \( -2; -6; -18;\text{______};\text{______};\text{______}\)
3. \(100; -50; 25;\text{______};\text{______};\text{______}\)
4. \(3; 4; 7; 11;\text{______};\text{______};\text{______}\)
In this question, you are given the rule by which each term of the sequence can be found. In all cases, \(n\) is the position of the term.
Determine the first three terms of each of the sequences. (Hint: Substitute \(n = 1\) to find the value of the first term.)
1. \(n \times 4\)
2. \(n\times 5 - 12\)
3. \(2 \times n^2\)
4. \(3n \div 3 \times -2\)
Write down the rule by which each term of the sequence can be found (in a similar format to those given in question 2, where n is the position of the term).
1. \(2; 4; 6; ...\)
2. \(-7; -3; 1; ...\)
3. \(2; 4; 8; ...\)
4. \( 9; 16; 23; ...\)
Use the rules you have found in question 3 to find the value of the 20th term of the sequences in questions 3(a) and 3(b).

Find the relationship between the position of the term in the sequence and the value of the term, and use it to fill in the missing values in the tables.

Position in sequence	1	2	3	4		25
Value of the term	-8	-11	-14

Position in sequence	1	2	3
Value of the term	1	3	9		243		19 683

The image below shows a series of patterns created by matches.

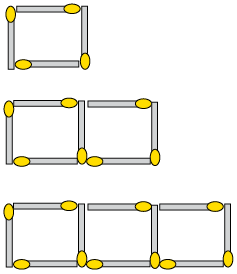
Write in words the rule that describes the number of matches needed for each new pattern.

Use the rule to determine the missing values in the table below, and fill them in.

Number of the pattern	1	2	3	4		20
Number of matches needed	4	7						151

Functions and relationships

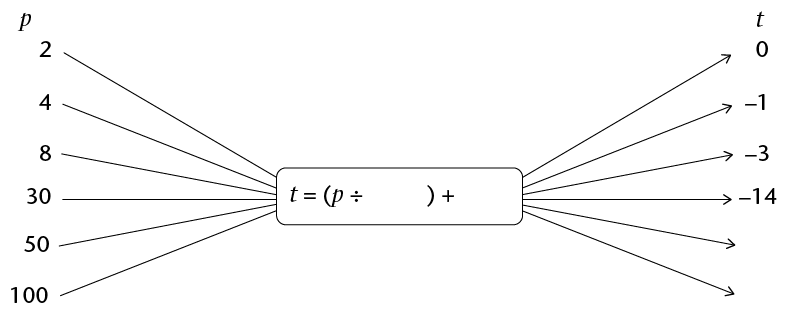
Fill in the missing input values, output values or rule in these flow diagrams. Note that \(p\) and \(t\) are integers.

Consider the values in the following table. The rule for finding \(y\) is: divide \(x\) by -2 and subtract 4. Use the rule to determine the missing values in the table, and write them in.

x			-2	0	2		5
y	-1		-3	-4					48

Consider the values in the following table:

\(x\)	-2	-1	0	1	2		4		15
\(y\)	1	3	5	7	9						61

Write in words the rule for finding the \(y\)-values in the table.
Use the rule to determine the missing values in the table, and write them in.

Algebraic expressions

Look at this algebraic expression: \(5x^3 - 9 + 4x - 3x^2\).
1. How many terms does this expression have?
2. What is the variable in this expression?
3. What is the coefficient of the \(x^2\) term?
4. What is the constant in this expression?
5. Rewrite the expression so that the terms are in order of decreasing powers of \(x\).
In this question, \(x=6\) and \(y = 17\). Complete the rules to show different ways to determine \(y\) if \(x\) is known. The first way is done for you:
Way 1: Multiply x by 2 and add 5. This can be written as \(y = 2x + 5\)
1. Way 2: Multiply \(x\) by ______ and then subtract ______. This can be written as
2. Way 3: Divide \(x\) by ______ and then add ______ . This can be written as
3. Way 4: Add ______ to \(x\), and then multiply by ______ . This can be written as
Simplify:
1. \(2x^2 + 3x^2\)
2. \(9xy -12xy\)
3. \(3y^2 - 4y + 3y - 2y^2\)
4. \(9m^3 + 9m^2 + 9m^3 - 3\)
Calculate the value of the following expressions if \(a = -2; b = 3; c = -1 \text{ and } d = 0:\)
1. \(abc\)
2. \(-a^2\)
3. \((abc)^d\)
4. \(a + b- 2c\)
5. \((a + b)^{10}\)

Algebraic equations

Write equations that represent the given information:
1. Nandi is \(x\) years old. Shaba, who is \(y\) years old, is three years older than Nandi.
2. The temperature at Colesberg during the day was \(x\)°C. But at night, the temperature dropped by 15 degrees to reach -2°C.
Solve the following equations for \(x\):
1. \(x + 5 = 2\)
2. \(7 - x = 9\)
3. \(3x - 1 = -10\)
4. \(2x^3 = -16\)
5. \( 2^x = 16\)
6. \( 2(3)^x = 6\)
If \(3n - 1 = 11\), what is the value of \(4n\)?
If \(c = a + b\) and \(a + b + c = 16\) , determine the value of \(c\).
1. If \(2a + 3 = b\), write down values for \(a\) and \(a\) that will make the equation true.
2. Write down a different pair of values to make the equation true.

Assessment

In this section, the numbers in brackets at the end of a question indicate the number of marks the question is worth. Use this information to help you determine how much working is needed. The total number of marks allocated to the assessment is 60.

The profits of GetRich Inc. have decreased in the ratio 5 : 3 due to the recession in the country. If their profits used to be R1 250 000, how much are their profits now?
Which car has the better rate of petrol consumption: Ashley's car, which drove 520 km on 32â„“ of petrol, or Zaza's car, which drove 880 km on 55â„“ of petrol? Show all your working.
Hanyani took out a R25 000 loan from a lender that charges him 22% interest each year. How much will he owe in one year's time?

Consider the following exchange rates table:

South African Rand	1.00 ZAR	inv. 1.00 ZAR
Indian Rupee	5.558584	0.179902
Australian Dollar	0.102281	9.776984
Canadian Dollar	0.101583	9.844200
Emirati Dirham	0.360838	2.771327
Chinese Yuan Renminbi	0.603065	1.658195
Malaysian Ringgit	0.303523	3.294646

Chen returns from a business trip to Malaysia with 2 500 ringgit in his wallet. If he changes this money into rand in South Africa, how much will he receive?

Fill <, > or = into the block to show the relationship between the number expressions:
1. \(6 - 4\) ☐ \(4 - 6\)
2. \(2 \times -3\) ☐ \(-3^2\)
Look at the number sequence below. Fill in the next term into the block.
\(-5; 10; -20\);☐
Calculate the following:
1. \( (-4)^2 - 20\)
2. \(\sqrt[3]{-8} + 14 \ \div 2\)
Julius Caesar was a Roman emperor who lived from 100 BC to 44 BC. How old was he when he died?
1. Write down two numbers that divide to give an answer of -8. One of the numbers must be positive, and the other negative.
2. Write down two numbers that subtract to give an answer of 8. One of the numbers must be positive and the other negative.
Write the following number in scientific notation: 17 million.
Which of the following numbers is bigger: \(3,47 \times 10^{21} \text{ or }7,99 \times 10^{20}\)?
Simplify the following, leaving all answers with positive exponents:
1. \( 3^7 \times 3^-2\)
2. \((-12y^8) \div (-3y^2)\)
3. \( \frac{(3xy^2z^3)(-yz)^2}{15x^5y^4z^7}\)
Write down the values of each of the following:
1. \((0.3)^3\)
2. \( 8 \sqrt{\frac{25}{16}} \)
Consider the following number sequence: \(2; -8; 32; ...\)
1. Write in words the rule by which each term of the sequence can be found.
2. Write the next three terms in this sequence.

The picture below shows a series of patterns created by matches.

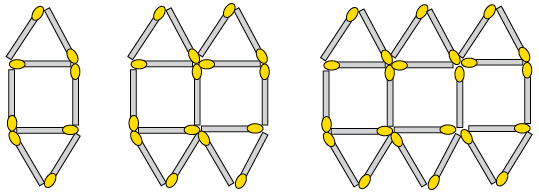
Write a formula for the rule that describes the relationship between the number of matches and the position of the term in the sequence (pattern number). Let \(n\) be the position of the term.

Use the rule to determine the values of \(a\) to \(c\) in the following table:

Number of the pattern	1	2	3	4		15		c
Number of matches needed	8	15	22	a		b		148